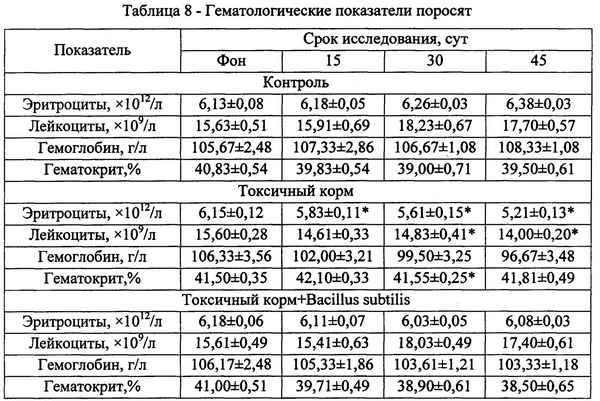
УНИВЕРСАЛЬНЫЙ ХАРАКТЕР РЕКУРРЕНТНЫХ ЗАВИСИМОСТЕЙ ФИЗИКО-ХИМИЧЕСКИХ СВОЙСТВ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ

Возможности применения линейных рекуррентных уравнений первого порядка A(n+1) = aA(n) + b для аппроксимации пpaктически любых констант органических соединений выходят за пределы локальных групп гомологов. Единые уравнения этого вида описывают вариации свойств всех гомологов любых рядов. Более того, рекуррентные соотношения применимы к функциям не только целочисленных (число атомов углерода в молекуле, n), но и равноотстоящих значений непрерывных аргументов (температура, давление, состав) A(x+Δx) = aA(x) + b, (Δx = const), что позволяет распространить их на температурные зависимости растворимости различных веществ в воде и даже времени релаксации в высокочастотных полях.
Рекуррентные соотношения, определяющие каждое из чисел различных последовательностей как функцию предыдущих члeнов тех же последовательностей, хорошо известны в математике. В соответствии с таким определением, они применимы только к функциям целочисленных аргументов. Удивительно, что до 2005 г. примеры их использования в химии неизвестны, хотя одним из самых «естественных» целочисленных аргументов является число атомов углерода в молекулах гомологов органических соединений (n). Первые же попытки [1,2] применения простейших линейных (первого порядка) рекуррентных соотношений вида (1) к разным свойствам гомологов показали, что они обеспечивают аппроксимацию физико-химических констант органических соединений в пределах различных таксономических групп с коэффициентами корреляции (r) выше 0.999, т.е. с точностью, сравнимой с современным уровнем межлабораторных погрешностей их определения:
A(n+1) = a A(n) + b (1)
Уравнение (1) применимо к различным свойствам не только однорядных нормальных линейных гомологов (с общей формулой RX, где Х - постоянная для ряда функциональная группа или фрагмент структуры, R = CnH2n+1 = варьируемый алкильный радикал), но и в пределах групп многорядных гомологов (RnY, n > 1), равно как внедрения [X(CH2)nY, n ≠ const] и циклических [цикло-(CH2)nZ, n ≠ const ] [3]. Более того, установлено, что степень общности соотношений вида (1) существенно выходит за пределы перечисленных локальных таксономических групп. Они применимы для аппроксимации констант гомологов любых рядов при условии постоянства гомологических разностей (прежде всего, СН2).
На рис. 1а представлена графическая иллюстрация единой рекуррентной зависимости нормальных температур кипения (Ткип) соединений 10 наиболее подробно охаpaктеризованных гомологических рядов (алканы, алкены, арены, все алкилгалогениды RHal, Hal = F, Cl, Br, I, алканолы, алканали и алканоны) в диапазоне температур от -50 до 350 0С (общее число точек 189) [1]. Параметры уравнения (1) для этой совокупности данных равны:
a = 0.930 ± 0.002; b = 33.5 ± 0.3;
r = 0.9995; S0 = 2.4
Такая линейная зависимость эквивалентна существованию универсального простого метода оценки Ткип пpaктически любых органических соединений на основании данных для предыдущих гомологов с точностью не хуже S0. Например, для предсказания Ткип N-гексиланилина C6H5NHC6H13 необходимо располагать справочным значением Ткип предшествующего гомолога - N-пентиланилина (260 0С), после чего выполнить простейшие арифметические действия:
0.93 x 260 + 33.5 ≈ 275.3
(справочное значение Ткип N-гексилани-лина 275 0С).
Аналогичное единое рекуррентное соотношение хаpaктеризует гомологичес-кие вариации Ткип перфторированных органических соединений RFX (перфторалканы, алкены, карбоновые кислоты, метилперфторал-каноаты и все перфторалкилгалогениды RFHal, Hal = Cl, Br, I). При этом коэффициенты уравнения (1) для рядов с гомологической разностью CF2 оказываются иными, чем приведенные выше коэффициенты для рядов с гомологической разностью СН2 (диапазон вариаций Ткип от -80 до 200 0С, число точек 24):
a = 0.893 ± 0.005; b = 32.1 ± 0.3;
r = 0.9997; S0 = 1.9
Следовательно, природа не функциональных групп, а именно гомологической разности определяет коэффициенты единых рекуррентных уравнений для разных рядов. Графическая иллюстрация зависимости (1) для Ткип перфторпроизводных представлена на рис. 1б.
В продолжение хаpaктеристики возможностей аппроксимации разнообразных свойств органических соединений едиными рекуррентными соотношениями для разных рядов, на рис. 2а приведен график подобной зависимости для диэлектрических проницаемостей (e, безразмерные величины) гомологов 11 рядов со следующими параметрами:
a = 0.759 ± 0.005; b = 1.03 ± 0.07;
r = 0.9988; S0 = 0.3 (55 точек)
На Рис. 2б представлен график аналогичной зависимости для значений динамической вязкости (hs, спз, 20 0С) соединений 11 рядов, параметры которого равны:
a = 1.22 ± 0.01; b = 0.03 ± 0.01; r = 0.9989; S0 = 0.04 (38 точек)
Единые рекуррентные уравнения, хаpaктеризующие вариации констант любых гомологов, существуют не только для перечисленных, но и для других свойств органических соединений. Это означает, что для оценки значений пpaктически любых констант любых органических соединений с использова-нием данных для предыдущих гомологов вместо большого числа разнообразных и уникальных методов [4] может быть использован единый универсальный алгоритм, основаный на применении рекуррентных соотношений (1). Такой уровень обобщений в химии достигнут впервые.
Дальнейшее расширение возмож-ностей применения рекуррентных соотношений связано с их распростраением на непрерывные свойства (температура, давление, состав). Во всех таких случаях рекуррентные уравнения применимы только к равноотстоящим значениям аргумента (т.е. при Δx = const):
а) б)
Рис. 1. (а) - Графическая иллюстрация единой линейной рекуррентной зависимости Tкип(n+1) = a Ткип(n) + b нормальных температур кипения соединений 10 рядов с гомологическими разностями СН2; (б) - то же для соединений семи рядов с гомологическими разностями CF2.
а) б)
Рис. 2. (а) - Графическая иллюстрация единой рекуррентной зависимости e(n+1) = a e(n) + b диэлектрических проницаемостей соединений 11 гомологических рядов; (б) - то же для зависимости hs(n+1) = a hs(n) + b динамической вязкости гомологов 11 рядов.
A(x+Δx) = a A(x) + b (2)
Подобное казалось бы незначительное изменение формы записи открывает совершенно новые области применения этих уравнений, например, позволяет хаpaктеризовать температурные зависимости растворимости различных веществ.
Вариации растворимости неогра-нических солей (чаще всего увеличивается), газов (уменьшается) и органических соединений (известны разные типы зависимостей) в воде при повышении температуры хорошо известны. Менее известно, что удовлетворительная аппроксимация таких зависимостей возможна только с использованием полиномов (степени n ³ 2), либо с применением достаточно «экзотических» функций, например lgy = a + b/T + сlgT, где y - мольная доля растворенного вещества, Т - абсолютная температура, К [5]. Например, для такой соли как KCl, коэффициенты приведенного уравнения равны: a = 6.75911, b = -604.3346, c = -2.357042, что дает, например, при 60 0С у = 0.100 (экспериментальное значение 0.099). Однако все данные по растворимости (выраженные непосредственно в масс. %, пересчет в мольные доли при этом не требуется) с высокой точностью могут быть аппроксимированы линейными рекуррентными уравнениями первого порядка вида (2). В Табл. 1 приведены результаты такой обработки для нескольких неорганических солей [6] (х = Т, DТ = 20 0С). Во всех случаях коэффициенты корреляции превышают 0.999, а значения генеральной дисперсии S0, хаpaктеризующие среднюю точность аппроксимации, варьируют в пределах 0.08-0.3, что составляет для большинства солей всего 0.2-0.6 % их растворимости при 20 0С.
Таблица 1. Рекуррентная аппроксимация температурной зависимости растворимости некоторых неорганических солей в воде
|
Соль |
Растворимость, масс. % при различной температуре, 0С |
Параметры уравнения (2) при DТ = 20 0С |
||||||||
|
0 |
20 |
40 |
60 |
80 |
100 |
a |
b |
r |
S0 |
|
|
BaCl2´2H2O |
24.0 |
26.3 |
29.0 |
31.7 |
34.4 |
37.0 |
1.02±0.02 |
2.0±0.6 |
0.9993 |
0.17 |
|
KCl |
22.2 |
25.5 |
28.7 |
31.3 |
33.8 |
36.0 |
0.90±0.01 |
5.6±0.4 |
0.9997 |
0.12 |
|
KIO3 |
4.5 |
7.5 |
11.4 |
15.6 |
19.9 |
24.4 |
1.08±0.03 |
3.0±0.3 |
0.9992 |
0.3 |
|
NH4Cl |
23.0 |
27.3 |
31.4 |
35.6 |
39.6 |
43.6 |
0.98±0.01 |
4.6±0.2 |
0.9999 |
0.08 |
|
(NH4)2SO4 |
41.4 |
43.0 |
44.8 |
46.8 |
48.8 |
50.8 |
1.05±0.02 |
-0.5±0.8 |
0.9996 |
0.10 |
|
Pb(NO3)2 |
26.7 |
34.3 |
41.0 |
46.8 |
51.8 |
56.0 |
0.87±0.01 |
11.3±0.2 |
0.9999 |
0.08 |
Однако, в отличие от задач аппроксимации свойств гомологов органических соединений, для функций непрерывных аргументов часто требуется оценка соответствующих величин при любых промежуточных, а не обязательно равноотстоящих значениях аргументов. В рассматриваемом примере это растворимость солей в воде при температурах не кратных 20 0С. Любой расчетный метод в общем случае должен предусматривать получение таких решений.
Известно, что рекуррентное уравнение (1) имеет следующее алгебраическое решение [1-3]:
A(n) = kan + b(an-1) / (a-1) (3)
которое позволяет вычислять значения A(n) для любых n при известных k, a и b. Дополнительный параметр k можно получить из выражения (1) для первого члeна последовательности, т.е. значения свойства А для простейшего рассматриваемого гомолога: А(1) = ka + b, откуда следует:
k = [A(1) - b] / a (4)
Тогда, например, для растворимости такой соли как BaCl2´2H2O в воде получаем k = 21.57, а решение уравнения (3) становится возможным для любых температур в интервале 0-100 0С с ошибками не более ± 0.1-0.2:
|
Температура, 0С |
Экспериментальное значение растворимости, масс % |
Рассчитанное значение растворимости, масс. % |
Ошибка |
|
0 |
24.0 |
24.0 |
0.0 |
|
20 |
26.3 |
26.5 |
+0.2 |
|
40 |
29.0 |
29.0 |
0.0 |
|
60 |
31.7 |
31.6 |
-0.1 |
|
80 |
34.4 |
34.2 |
-0.2 |
|
100 |
37.0 |
36.9 |
-0.1 |
|
30 |
- |
27.7 |
- |
|
50 |
- |
30.3 |
- |
Аналогичным образом рекуррентные соотношения первого порядка применимы для аппроксимации убывающих с увеличением температуры растворимостей газов в воде [7]. В табл. 2 представлены соответствующие экспериментальные данные и параметры рекуррентных уравнений (3) при DТ = 20 0С. Как и в случае неорганических солей, коэффициенты корреляции во всех случаях превышают 0.999.
Таблица 2. Рекуррентная аппроксимация температурной зависимости растворимости некоторых газов в воде
|
Соединение |
Растворимость (мл/100 г) при различной температуре, 0С |
Параметры уравнения (2) при DТ = 20 0С |
||||||||
|
0 |
20 |
40 |
60 |
80 |
100 |
a |
b |
r |
S0 |
|
|
Азот |
2.35 |
1.54 |
1.18 |
1.02 |
0.96 |
0.95 |
0.43±0.01 |
0.52±0.01 |
0.9992 |
0.01 |
|
Кислород |
4.89 |
3.10 |
2.31 |
1.95 |
1.78 |
1.72 |
0.446±0.001 |
0.919±0.009 |
0.9993 |
0.008 |
|
Метан |
5.56 |
3.31 |
2.37 |
1.95 |
1.77 |
1.70 |
0.426±0.003 |
0.94±0.01 |
0.9999 |
0.01 |
|
Этан |
9.87 |
4.72 |
2.91 |
2.18 |
1.83 |
1.72 |
0.37±0.01 |
1.07±0.05 |
0.9990 |
0.06 |
|
Сероводород |
467 |
258 |
166 |
119 |
91.7 |
81 |
0.48±0.01 |
38 ± 3 |
0.9990 |
3.8 |
|
Оксид азота (II) |
7.38 |
4.71 |
3.51 |
2.95 |
2.70 |
2.63 |
0.45±0.01 |
1.39±0.02 |
0.9998 |
0.02 |
Столь универсальный хаpaктер рекуррентных соотношений, применимых для аппроксимации не только вариаций любых физико-химмических констант гомологов, но и, например, температурных зависимостей непрерывных свойств, может привести к существенному изменению методологии интерпретации данных во многих областях химии. Действительно, проверку корректности наборов различных величин нет необходимости начинать с создания уникальных физико-химических моделей соответствующих явлений. В качестве наиболее «экзотического» примера можно привести температурную зависимость времен релаксации (t) воды [8] являющихся важной хаpaктеристикой поведения веществ в высокочастотных электрических (при определении диэлектрических проницаемостей) и магнитных (в спектроскопии ЯМР) полях. Эквидистантные значения t (при неизвестных погрешностях сложных экспериментальных определений) в диапазоне температур 0-60 0С равны:
|
Т, 0С |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
t, пс |
17.7 |
12.6 |
9.2 |
7.1 |
5.7 |
4.8 |
3.9 |
Вне всяких сомнений, соответству-ющая модель, описывающая диссипацию внутримолекулярных энергий за счет межмолекулярных взаимодействий, весьма сложна. Однако, как проверка корректности приведенных данных, так и, при необходимости, расчет значений t при любых других температурах возможны с использованием простейшего рекуррентного соотношения:
τ(T + ΔT) = a τ(T) + b, (5)
где ΔT = 10 0С, a = 0.652 ± 0.006, b = 1.04 ± 0.06, r = 0.9998, S0 = 0.06
Более того, уникальные возможности рекуррентных соотношений иллюстрирует тот факт, что одно из значений τ = 3.9 пс, соответствующее Т = 60 0С, хуже всех согласуется с единой зависимостью (5). Незначительная коррекция этой величины (должно быть τ = 4.1) невозможна никаким другим методом кроме рассматриваемого.
СПИСОК ЛИТЕРАТУРЫ:
- Зенкевич И.Г. Общие закономерности изменения физико-химических свойств органических соединений в гомологических рядах // Журн. органич. химии. 2006. Т. 42. № 1. С. 9-20.
- Зенкевич И.Г. Единый закон вариаций любых свойств органических соединений в гомологических рядах. // Успехи совр. естествозн. 2006. № 7. С. 42-46.
- Зенкевич И.Г. Использование рекуррентных соотношений для аппроксимации свойств любых гомологов органических соединений. // Журн. общей химии. 2006. Т. 76. Вып. 11. С. 1821-1833.
- Рид Р., Шервуд Т. Свойства газов и жидкостей (определение и корреляция). / Пер. с англ. Л.: Химия, 1971. 703 с.
- Broul M., Nyvlt J., Sohnel O. Solubility in Inorganic Two-Component Systems. Amsterdam: Elsevier, 1981.
- Краткий справочник химика. Сост. В.И.Перельман. 7 изд. М.-Л.: Химия, 1964. 623 с.
- Лидин Р.А., Андреева Л.Л., Молочко В.А. Справочник по неорганической химии. М.: Химия, 1987. 320 с.
- Kaatze U., Uhlendorf V. The Dielectric Properties of Water at Microwave Frequences. // Z. Phys. Neue, Folge. 1981. V. 126. P. 151-165. Цит. по http://www.kayelaby.npl.co.uk/general_physics/2_6/2_6_5.html
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
19 04 2024 5:15:17
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
18 04 2024 10:59:44
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
17 04 2024 8:21:19
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
16 04 2024 12:13:39
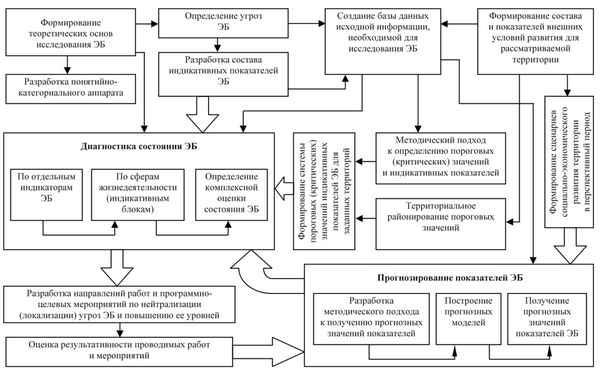
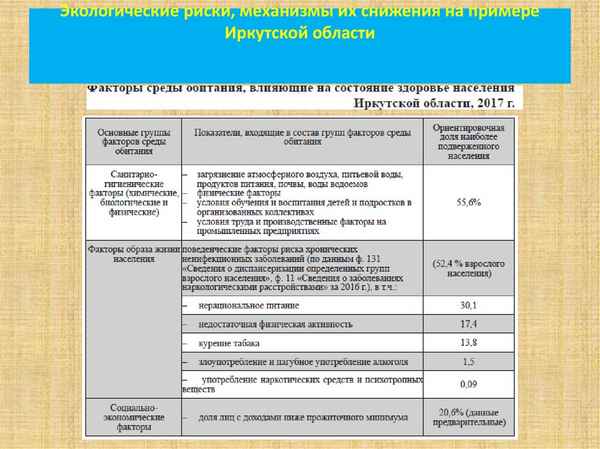 В статье представлена комплексная оценка экологического риска территории Иркутской области. Наличие в области большого количества промышленных объектов с опасными производствами, технологиями и материалами предопределяет реальную возможность возникновения техногенных аварий и катастроф. Естественными природными факторами риска являются землетрясения, оползни, ураганы, наводнения, лесные пожары, опасные инфекционные заболевания, эпизоотии и эпифитотии. Более того, многие природные ЧС возникают как следствие воздействия человека на природную среду. Городская экосистема должна проектироваться и развиваться на основе технологии комплексной оценки экологической емкости территорий, которая необходима для гармоничного развития территорий без деградации природных экосистем любого уровня. В Иркутской области наблюдается значительное загрязнение всех компонентов окружающей среды, что также сказывается на показателях состояния здоровья населения. Выявлена статистически значимая связь между показателями детской cмepтности и загрязнением природной среды. Комплексная оценка экологического риска по предлагаемой методике показывает, что природная среда исследуемой территории уже никогда не сможет восстановиться в первоначальном виде.
...
В статье представлена комплексная оценка экологического риска территории Иркутской области. Наличие в области большого количества промышленных объектов с опасными производствами, технологиями и материалами предопределяет реальную возможность возникновения техногенных аварий и катастроф. Естественными природными факторами риска являются землетрясения, оползни, ураганы, наводнения, лесные пожары, опасные инфекционные заболевания, эпизоотии и эпифитотии. Более того, многие природные ЧС возникают как следствие воздействия человека на природную среду. Городская экосистема должна проектироваться и развиваться на основе технологии комплексной оценки экологической емкости территорий, которая необходима для гармоничного развития территорий без деградации природных экосистем любого уровня. В Иркутской области наблюдается значительное загрязнение всех компонентов окружающей среды, что также сказывается на показателях состояния здоровья населения. Выявлена статистически значимая связь между показателями детской cмepтности и загрязнением природной среды. Комплексная оценка экологического риска по предлагаемой методике показывает, что природная среда исследуемой территории уже никогда не сможет восстановиться в первоначальном виде.
...
14 04 2024 11:38:25
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
13 04 2024 12:22:30
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
12 04 2024 12:40:20
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
09 04 2024 22:31:26
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
08 04 2024 0:35:47
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
07 04 2024 15:34:17
 Статья в формате PDF
327 KB...
Статья в формате PDF
327 KB...
06 04 2024 16:10:48
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
05 04 2024 6:22:47
 Статья в формате PDF
282 KB...
Статья в формате PDF
282 KB...
03 04 2024 1:52:41
 Статья в формате PDF
140 KB...
Статья в формате PDF
140 KB...
02 04 2024 2:58:21
 Статья в формате PDF
310 KB...
Статья в формате PDF
310 KB...
01 04 2024 13:30:41
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
30 03 2024 17:52:40
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
28 03 2024 18:26:42
27 03 2024 21:16:47
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
26 03 2024 21:34:34
25 03 2024 21:29:32
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
24 03 2024 15:34:42
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
23 03 2024 10:43:45
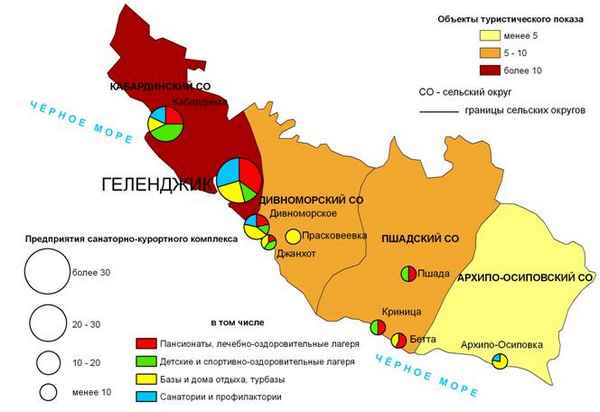
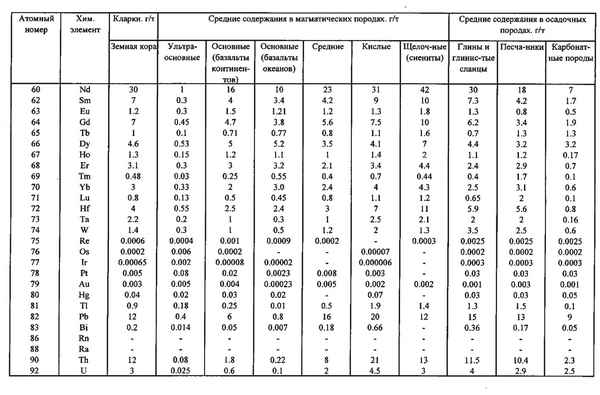 Известные способы предполагают проведение испытаний травяно-кустарничкового покрова на содержание химических элементов на пробных площадках. Недостатком является раздельная обработка результатов испытаний, что лишает возможности совместного изучения травы и древесных растений. В статье показаны возможности повышения точности изучения комплекса «трава + древесное растение», а также сопоставимости содержания химических элементов по высоте растений.
...
Известные способы предполагают проведение испытаний травяно-кустарничкового покрова на содержание химических элементов на пробных площадках. Недостатком является раздельная обработка результатов испытаний, что лишает возможности совместного изучения травы и древесных растений. В статье показаны возможности повышения точности изучения комплекса «трава + древесное растение», а также сопоставимости содержания химических элементов по высоте растений.
...
22 03 2024 15:35:42
 Слепая кишка морской свинки имеет форму витка толстой спирали и большие относительные размеры, занимает большую часть каудальной половины брюшной полости, охвачена первой петлей восходящей ободочной кишки. Она сжимает слепую кишку, которая образует складки.
...
Слепая кишка морской свинки имеет форму витка толстой спирали и большие относительные размеры, занимает большую часть каудальной половины брюшной полости, охвачена первой петлей восходящей ободочной кишки. Она сжимает слепую кишку, которая образует складки.
...
20 03 2024 0:57:21
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
19 03 2024 18:38:29
18 03 2024 14:39:23
 Статья в формате PDF
141 KB...
Статья в формате PDF
141 KB...
17 03 2024 4:16:39
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
16 03 2024 6:17:49
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
15 03 2024 4:21:37
 Статья в формате PDF
255 KB...
Статья в формате PDF
255 KB...
14 03 2024 23:27:52
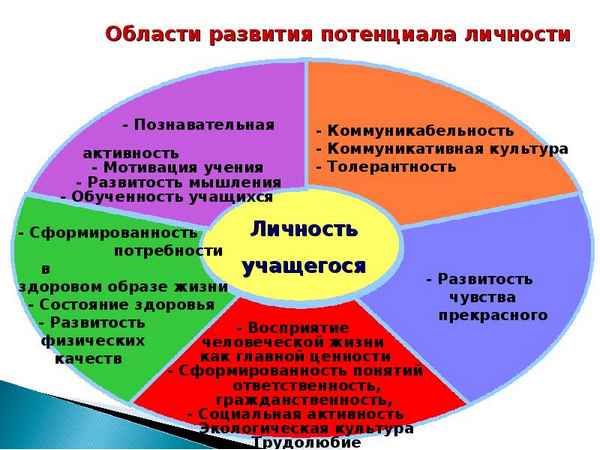 В данной статье осуществлены анализ и обощение зарубежных психологических концепций, объясняющих активность человека в отношении своего здоровья, и на этой основе дано авторское определение понятия «здоровьесозидающий потенциал личности». Особое внимание авторы уделяют рассмотрению структуры здоровьесозидающего потенциала, описанию психологических механизмов его формирования и выявлению закономерностей его развития в различные возрастные периоды. Авторами впервые представлена и научно обоснована векторная модель здоровьесозидающего потенциала личности, показаны её возможности при выявлении психологических детерминант, влияющих на показатели целостного здоровья человека.
...
В данной статье осуществлены анализ и обощение зарубежных психологических концепций, объясняющих активность человека в отношении своего здоровья, и на этой основе дано авторское определение понятия «здоровьесозидающий потенциал личности». Особое внимание авторы уделяют рассмотрению структуры здоровьесозидающего потенциала, описанию психологических механизмов его формирования и выявлению закономерностей его развития в различные возрастные периоды. Авторами впервые представлена и научно обоснована векторная модель здоровьесозидающего потенциала личности, показаны её возможности при выявлении психологических детерминант, влияющих на показатели целостного здоровья человека.
...
13 03 2024 9:56:54
 Статья в формате PDF
254 KB...
Статья в формате PDF
254 KB...
12 03 2024 23:33:26
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
11 03 2024 16:49:50
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::