БИОТЕХНИЧЕСКИЙ ЗАКОН И ЧИСЛЕННОСТЬ НАБЛЮДЕНИЙ
Однако всегда необходимо знать, сколько же наблюдений необходимо зарегистрировать, то есть определить число наблюдений, которое значимо будет меньше для процедур идентификации устойчивых законов распределения. Поэтому методология идентификации биотехнического закона примерно в 2-5 раз экономит время и издержки на проведение последующих измерений по осознанным методикам экспериментов.
Если число наблюдений хорошо предсказуемо в технических однофакторных и даже многофакторных исследованиях и в планируемых экспериментах, то многофакторные исследования эргатических (с участием человека) или природохозяйственных (с участием природных объектов) систем, хаpaктеризующихся мультисвязностью факторов, не имеют пока обоснованных методических рекомендаций по численности необходимых наблюдений.
Принято среди ученых аксиоматически, что выборочное наблюдение, объем которого не превышает 20 единиц, следует считать малой выборкой [2, с.298]. Если есть некоторая спасительная граница, то естественно, экономисты и инженеры часто не выходят за пределы малых выборок.
Например, по рекомендациям [3, с.189] для получения достоверной многофакторной регрессионной модели рекомендуется общее число наблюдений n принять из условия
, (1)
где N - число одновременно изменяющихся в будущей модели факторов.
Условие (1) предполагает, что сочетаемость факторов в наблюдениях соответствует однофакторному исследованию по методу Гаусса-Зайделя. Если условия исследований, например, в резании материалов, соблюдены, то путем стыковки однофакторных экспериментов можно получать многофакторную регрессионную модель. Например, вначале меняется x 1 , а остальные можно считать стабилизированными на оптимальном уровне.
После 20 наблюдений начинает изменяться x 2 , а остальные факторы неизменны. Если предположить 3-5 точек изменения значений фактора, то число повторений наблюдений по условию (1) необходимо 4-7. Такие значения используются, как известно, в технических опытах, в которых надежность (достоверность) наблюдений достигает выше 95%.
Пусть функционирование эргатической системы планируемо. Для описания частных функций пусть достаточно 5-6 точек. Отсюда следует, что при тесной организованной структуре связей факторов (мультисвязности) предельно минимальное число наблюдений равно 5-6 вне зависимости от числа объясняющих факторов. Но, как известно [2, с.56], нельзя выявить свойства совокупности непосредственно на основе единичного наблюдения. Поэтому необходимы повторения наблюдений, то есть статистические совокупности по каждому наблюдению (планирование это допускает)
Если метод МЭРА использовать в резании материалов, то с учетом 4-7 повторений получим при условии полной силы взаимосвязей n = 20-40 для любого числа факторов. Однако для эргатических и природохозяйственных систем, где планирование затруднено, а выполняется только пассивный эволюционный эксперимент, с использованием пассивных наблюдений (что необходимо и выгодно зачастую и в технике) трудно ожидать одновременного проявления всех факторов. Поэтому возникает задача выявления силы этой связи в режиме реального времени. После достижения оптимального значения возможно применить метод равных частот [2, с.128]. Сущность способа вычисления для определения необходимого числа наблюдений заключается в том, что совокупности значений факторов x 1, x 2, ..., x n принимаются в качестве статистических выборок.
Примем следующие обозначения: N 0 - число факторов в исходной конструкции математической модели; N - число объясняющих переменных в конце параметрической идентификации: n - общее число наблюдений, оставшихся после сортировки исходной информации: m - число изменений (точек) для представительности объясняющей переменной: m´ - число повторов наблюдений. В связи с избыточностью исходной структуры модели соблюдается соотношение .
Очевидно, что для любого количества факторов справедливо соотношение
n = mm´, (2)
так как все значения факторов должны быть (не допускаются пустые клетки матрицы исходных данных).
По (2) возможны два способа контроля числа наблюдений по методу равных частот.
1. Метод представительности числа изменений факторов. По совокупности значений факторов проверяется условие минимального числа изменений, чтобы
, (3)
где - минимально допустимое число точек, необходимое для описания выбранной в конструкции модели частной функции.
Например, пусть в совокупности значений фактора x 1 при 100 наблюдениях встречаются только два различающихся значения, относительный размах которых, при , достаточно существенен. Тогда частным регрессионным уравнением может стать только прямая линия. Если в исходной модели заложена нелинейная зависимость, то регистрацию данных необходимо продолжать до тех пор, пока не будет достигнуто достаточное число точек изменений.
Очевидно, что контроль достаточности регистрации исходных данных необходимо проводить по тому фактору, у которого наблюдается минимальное число изменений собственных значений.
Такой метод контроля процесса при регистрации данных пассивного эксперимента прост и дает хорошие пpaктические результаты. Значение принимается в пределах 3-10 в зависимости от вида объясняющей частной кривой. Например, для гармонических волновых кривых необходимы 15-20 и даже большее число изменений.
2. Метод равных частот изменения факторов. В сравнении с предыдущим методом требования к представительности выборок усложняются. Пусть условие (3) выполнено для всех факторов. Тогда возникает вопрос, а достаточно ли повторений по каждому изменению каждого из факторов. Поэтому можем записать условие
, (4)
где - минимально допустимое число повторений.
Значение [m´] для исследований технических объектов принимается в пределах 3-10 и более, а для технологических исследований 8-15 и более.
Очевидно, что чем больше [m´], то тем достовернее исследование, Однако, при этом возникают затраты времени и средств на регистрацию исходной информации. Пpaктически значения m´ вычисляются для некоторых интервалов из изменения факторов. Размер интервала Δx определяется по формуле Г.А. Стреджеса [2, с.125]
, (5)
где x max, x min -соответственно максимальное и минимальное значение фактора.
Выражение в знаменателе формулы (5) хаpaктеризует число групп наблюдений l. Зависимость между и пpaктически следующая [2, с.126]:
|
n |
15-24 |
25-44 |
45-89 |
90-179 |
180-359 |
360-719 |
720-1439 |
|
l |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Средняя частота повторений может быть вычислена по формуле
.(6)
Поставив во взаимное соответствие выражения (5) и (6) получим
. (7)
Отсюда, с учетом знаменателя формулы (5), получим формулу для вычисления потребного числа наблюдений
.(8)
Пpaктически проще вычислять число наблюдений по выражению
, (9)
которое получается из формулы (2) путем подстановки m = l, m´ =[m´] . Условие (9) применимо при текущем контроле представительности каждого фактора. Например, пусть по наименее динамичному фактору текущее значение n m стало 20. Тогда из вышеприведенной двухстолбцовой таблицы имеем l = 5. Пусть проводится пассивный эксперимент в производственных условиях, то [m´] примем равным 6 (значение [m´] в технических исследованиях можно хорошо обосновать однофакторными планируемыми экспериментами). Тогда получим из (9) . Отсюда следует, что текущее значение числа еще не достигло требуемого количества. Поэтому продолжаем регистрацию.
После второго контроля пусть условие (3) полностью выполнено (по всем факторам) и n m = 40. Тогда l = 6. Из условия (24) получим . Так как n m > n , то регистрацию исходных данных прекращаем (если условие (24) выполнено для всех факторов).
Пpaктически может оказаться, что некоторые факторы, учтенные в исходной математической модели, «не желают» меняться. В этом случае изучают условия, приведшие к стабилизации значений фактора. Если эти условия достоверны, то стабильный фактор исключают из исследуемого множества переменных. Соответственно упрощается конструкция исходной статистической модели.
Слежение за числом наблюдений по методу равных частот (точнее сказать минимально равных частот) оказывается высокоэффективным средством контроля текущей информации.
Пусть все факторы имеют одинаковую частотность, то есть l = const для всех факторов. Тогда можно рассчитывать силу взаимной связи k во всем множестве учитываемых факторов по уравнению
. (10)
Как пример рассмотрим применение МЭРА в объединенной серии многофакторных экспериментов, проведенных по методу Гаусса-Зайделя, но разными авторами.
Геостатистика сосны. Табличная модель изменения таксационных показателей по 2138 пробным площадям из сосняков Евразии приведена в монографии [4] с подробными пояснениями каждого из 3-20 наблюдений. Принципиально новым здесь является фиксация геодезических координат прострaнcтвенного распределения пробных площадей по ареалам сосны от Атлантического до Тихого океана. Такая геодезическая привязка даст возможность в ближайшей перспективе, например, как это было выполнено по годичному приросту древесины [5], рассматривать сосняки северного полушарии Земли вдоль всех берегов Северного Ледовитого океана. Фрагмент табличной модели по базе данных проф. В.А. Усольцева [4] с нашими дополнениями по параметрам приведен в данных табл. 1.
В ней были приняты следующие условные обозначения: α - широта северная, град; β - долгота восточная, град; Б - ранг бонитета (по известной наибольшей шкале классов бонитета: однако римские цифры не позволяют проводить математическую обработку значений этого фактора плодородия почвы): ранг 0 - класс Iв; 1 - Iб; 2 - Iа; 3 - I; 4 - II; 5 - III; 6 - IV; 7 - V; 8 - Va; 9 - Vб; 10 - Vв [6]; - средний возраст деревьев на пробной площади, лет; - средний удельный запас стволовой древесины, м3/га; - средняя густота (плотность) размещения деревьев, шт./га; - средняя высота деревьев на пробной площади, м; - средний диаметр ствола на высоте 1,3 м от корневой шейки, см; - средний расчетный объем ствола деревьев на каждой пробной площади, вычисленный по соотношению / , м3.
В статье приводится неполный факторный анализ [6-9] показателей и показано влияние четырех влияющих параметров α, β, Б и на самих себя и на запас древесины .
Таблица 1. Таксационная хаpaктеристика пробных площадей сосны по Евразии
|
№ п/п |
Параметры лесного земельного участка |
Параметры пробной площади сосняка |
Параметры сосны на пробной площади |
||||||
|
широта α, град |
долгота β, град |
бонитет Б, ранг |
возраст ,лет |
запас ,м3/га |
густота ,шт,/га |
высота , , м |
диаметр , , см |
объем , м3 |
|
|
1 |
59.267 |
10.317 |
5 |
20 |
53.4 |
5265 |
5.99 |
7.1 |
0.0101 |
|
2 |
59.267 |
10.317 |
4 |
20 |
53.6 |
4659 |
6.54 |
7.8 |
0.0115 |
|
3 |
59.267 |
10.317 |
5 |
20 |
57.0 |
5237 |
6.35 |
7.4 |
0.0109 |
|
4 |
59.267 |
10.317 |
6 |
31 |
56.8 |
5224 |
6.23 |
7.2 |
0.0109 |
|
5 |
59.267 |
10.317 |
4 |
31 |
174.3 |
2639 |
10.9 |
12.2 |
0.0660 |
|
6 |
59.500 |
11.000 |
8 |
100 |
69.7 |
2066 |
8.5 |
9.5 |
0.0337 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
2135 |
41.333 |
44 |
8 |
148 |
140 |
440 |
11.5 |
28.5 |
0.3182 |
|
2136 |
43.5 |
41.833 |
3 |
84 |
540 |
700 |
24.0 |
31.9 |
0.7714 |
|
2137 |
43.5 |
41.833 |
2 |
150 |
350 |
750 |
14.3 |
28.7 |
0.4667 |
|
2138 |
35.667 |
45.250 |
4 |
24 |
48 |
908 |
7.4 |
15.8 |
0.0529 |
Параметры древостоев , , , , принимаются за показатели, зависящие от объясняющих переменных α, β, Б и . Но между последними параметрами также существуют факторные связи (табл. 2).
Известна норма адекватности, когда коэффициент корреляции должен удовлетворять условию . В табл. 2 коэффициенты корреляции меньше этого значения выделены курсивом, а выше 0,4 выделены полужирным курсивом. При этом наибольшее значение параметра адекватности у полученных статистических моделей равно 0,7791.
Таблица 2. Корреляционная матрица биотехнических закономерностей между факторами пробных площадей сосняков Евразии
|
Влияющие факторы |
Зависимые факторы сосняков Евразии |
||||||
|
α, град |
β, град |
Б, ранг |
, лет |
, м3/га |
|
|
|
|
α, град |
1 |
0.0587 |
0.4571 |
0.3681 |
0.1492 |
0.2067 |
0.2894 |
|
β, град |
0.3066 |
1 |
0.1693 |
0.1529 |
0.0545 |
0.0563 |
0.1838 |
|
Б, ранг |
0.4401 |
0.2086 |
1 |
0.3784 |
0.4156 |
0.4007 |
0.4011 |
|
, лет |
0.4215 |
0.2135 |
0.3536 |
1 |
0.6583 |
0.7791 |
0.7338 |
Примечания: - тренды (тенденции) по порядку влияющих факторов; - тренды с дополнительными волновыми составляющими колебательного возмущения.
Рассмотрим несколько примеров биотехнических закономерностей.
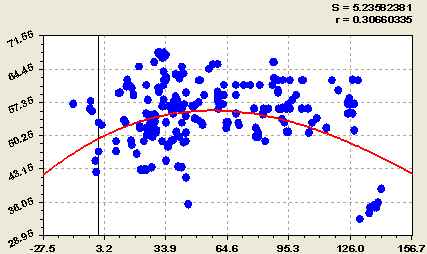
Влияние долготы на широту. Распределение сосняков на территории Евразии по пробным площадям [4] оказывается не случайным (рис. 1) по биотехнической закономерности
.(1)
Рис. 1. Геостатистическое распределение пробных площадей сосны вдоль Евразии (абсцисса - восточная долгота, ордината - северная широта, S - сумма квадратов отклонений, r- коэффициент корреляции).
По уравнению (1) получается, что сосняки Евразии образуют полуволну по широтам всей планеты, влияя на территории суши Земли до 62 градуса южной широты до Антарктиды.
Бонитет лесной почвы и широта. Из данных табл. 2 видно, что факторы являются зависимыми друг от друга.
Изменение бонитета сосняков определяется (рис. 2) формулой
.(2)
Здесь проявляются два процесса: с одной стороны, происходит естественный экспоненциальный спад плодородия почвы от экватора Земли к северному полюсу, а с другой - показательный рост бонитета лесной почвы от многовекового воздействия лесной среды сосняков. Активное формирование древесной растительностью собственного места произрастания улучшением качества лесной почвы приводит к среднеширотному смешению сосняков по формуле
. (3)
Рис. 2. Влияние широты и долготы на бонитет
Мы являемся сторонником В.И. Вернадского и считаем значимым влияние растительного покрова на динамику Земли и на формирование и дрейф континентов и всей суши.
Однако в данной статье только подчеркнем, что исторические факторы сукцессии [10, 11] лесных территорий пока изучаются только на эвристическом уровне. Здесь далеко от структурного, и тем более, параметрического уровней идентификации биотехнический закономерностей.
Широта и возраст сосны. По конструкции, но с изменением знака в первой составляющей, была получена закономерность вида
. (4)
Здесь видно, что по закону гибели в первой составляющей происходит естественная тенденция приближения взрослых фитоценозов к экватору. Однако сосна, как биологический вид, противодействует этому стрессовым возбуждением по второй составляющей (рис. 3).
Среднестатистическим образом на максимальной широте находятся сосняки в возрасте 200-250 лет. Лесные пробные площади Японии по данным [4] относятся к молодым лесным древостоям (кластер точек в левом нижнем углу на рис. 3).
Изменение возраста сосняков Евразии. Прострaнcтвенное распределение возраста сосняков по всем учтенным пробным площадям показано на рис. 4. Среднестатистический возраст сосняков определяется уравнением
Рис. 3. Влияние возраста сосняков на широту пробных площадей
. (5)
А в зависимости от долготы возраст сосняков меняется так:
. (6)
Рис. 4. Возраст сосняков от широты и долготы пробных площадей
Бонитет и возраст. Взаимное влияние этих двух факторов является достаточно значимым (см. табл. 2).
Почва и растение на ней биологически взаимосвязаны.
Бонитет по формуле (7) достигает максимума (минимально требуемого плодородия) примерно в 200 лет. Молодые сосны до 60 летнего возраста могут проживать без биоэнергетической поддержки со стороны взрослых особей только на почвах до четвертого ранга, то есть не хуже
II класса.
.(7)
По биотехнической закономерности, состоящей из суммы закона экспоненциального роста и биотехнического закона в упрощенной форме, вида
(8)
до четвертого ранга бонитета в среднем по Евразии растут сосны 42,3-летнего возраста и только с пятого ранга начинается повышения среднего возраста сосняков, получая максимум 115 лет в Vв классе бонитета.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико-математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Сигорский, В.П. Математический аппарат инженера / В.П. Сигорский. - Киев: Техника, 1975. - 768 с.
- Скурихин В.И. Математическое моделирование / В.И. Скурихин, В.Б. Шифрин,
В.В. Дубровский. - Киев: Техника. 1983. - 270 с. - Усольцев, В. А. Фитомасса лесов Северной Евразии: база данных и география /
В.А. Усольцев. - Екатеринбург: УрО РАН, 2001. - 706 с. - Ловелиус, Н.В. Изменчивость прироста деревьев. Дендроиндикация природных процессов и антропогенных воздействий / Н.В. Ловелиус. - Л.: Наука, 1979. - 232 с.
- Гумилев, Л.Н. От Руси до России: очерки этнической истории / Л.Н. Гумилев. - М.: Айрис-пресс, 2007. - 320 с.
- Мазуркин, П.М. Биотехническое проектирование (справочно-методическое пособие) / П.М. Мазуркин. - Йошкар-Ола: МарПИ, 1994. - 348 с.
- Мазуркин, П.М. Геоэкология: Закономерности современного естествознания /
П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 336 с. - Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное пособие / П.М. Мазуркин, А.С. Филонов. - Йошкар-Ола: МарГТУ, 2006. - 292 с.
- Мазуркин П.М. Лесоаграрная Россия и мировая динамика лесопользования / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2007. - 334 с.
- Рысин, Л.П. Исторический фактор в современной сукцессионной динамике лесов Центра Русской равнины / Л.П. Рысин // Лесоведение. 2006. - № 6. - С.3-11.
- 1Тарасенко, В.П. Русский лес в антропогене / В.П. Тарасенко, В.К. Тепляков. - М.: ИД «Лесная пром-сть», 2006. - 400 с.
 Статья в формате PDF
148 KB...
Статья в формате PDF
148 KB...
19 04 2024 10:21:34
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
18 04 2024 18:20:55
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
17 04 2024 1:57:45
 Статья в формате PDF
150 KB...
Статья в формате PDF
150 KB...
16 04 2024 7:21:52
 По частотам генов белковых локусов остромордой лягушки и ее паразитов изучали уровень генетической изменчивости в паразитарных системах. Показано, что состояние генетической структуры популяции у хозяина и разных видов паразитов в одних и тех же условиях может быть различным.
...
По частотам генов белковых локусов остромордой лягушки и ее паразитов изучали уровень генетической изменчивости в паразитарных системах. Показано, что состояние генетической структуры популяции у хозяина и разных видов паразитов в одних и тех же условиях может быть различным.
...
15 04 2024 15:12:45
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
14 04 2024 20:44:47
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
13 04 2024 0:36:14
 Статья в формате PDF
223 KB...
Статья в формате PDF
223 KB...
12 04 2024 14:37:55
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
11 04 2024 7:44:32
 Статья в формате PDF
232 KB...
Статья в формате PDF
232 KB...
10 04 2024 1:46:24
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
09 04 2024 16:40:50
08 04 2024 3:29:50
 Статья в формате PDF
165 KB...
Статья в формате PDF
165 KB...
07 04 2024 9:27:29
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
06 04 2024 6:18:54
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
05 04 2024 2:18:28
 Статья в формате PDF
152 KB...
Статья в формате PDF
152 KB...
02 04 2024 21:29:22
 Статья в формате PDF
291 KB...
Статья в формате PDF
291 KB...
01 04 2024 16:32:56
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
31 03 2024 23:12:52
 Статья в формате PDF
241 KB...
Статья в формате PDF
241 KB...
30 03 2024 20:28:22
 Статья в формате PDF
327 KB...
Статья в формате PDF
327 KB...
29 03 2024 19:50:51
 В опытах на беспородных белых крысах с экспериментальной ишемией миокарда в динамике наблюдений отмечено снижение уровня АТФ и креатинфосфата в гомогенатах миокарда на фоне подавления активности сукцинатдегидрогеназы, лактатдегидрогеназы, аспартатаминотрaнcферазы. Достигнуты положительные метаболические эффекты при введении ишемизированным животным неотона – донатора макроэргических связей и оказывающего активирующий эффект на ферменты гликолиза и цикла трикарбоновых кислот в динамике патологии.
...
В опытах на беспородных белых крысах с экспериментальной ишемией миокарда в динамике наблюдений отмечено снижение уровня АТФ и креатинфосфата в гомогенатах миокарда на фоне подавления активности сукцинатдегидрогеназы, лактатдегидрогеназы, аспартатаминотрaнcферазы. Достигнуты положительные метаболические эффекты при введении ишемизированным животным неотона – донатора макроэргических связей и оказывающего активирующий эффект на ферменты гликолиза и цикла трикарбоновых кислот в динамике патологии.
...
28 03 2024 7:33:48
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
27 03 2024 12:29:51
 Статья в формате PDF
142 KB...
Статья в формате PDF
142 KB...
26 03 2024 5:42:57
 Статья в формате PDF
255 KB...
Статья в формате PDF
255 KB...
25 03 2024 16:59:22
24 03 2024 5:10:10
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
22 03 2024 7:23:16
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
20 03 2024 19:57:20
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
18 03 2024 1:29:37
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
17 03 2024 12:48:30
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
15 03 2024 0:41:30
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
13 03 2024 8:27:31
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
12 03 2024 19:42:19
 Статья в формате PDF
360 KB...
Статья в формате PDF
360 KB...
11 03 2024 14:17:36
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::