ЛОГИСТИЧЕСКИЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ В ЗЕМЛЕДЕЛЬЧЕСКОЙ МЕХАНИКЕ

Авторы
Файлы

Богус Ш.Н. Букаткин Р.Н. Полумеев С.В. Статья в формате PDF 664 KB

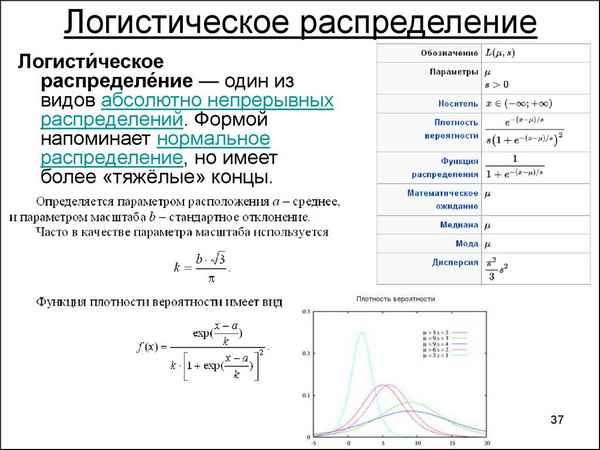
Под логистическим распределением вероятностей с функцией распределения, понимается распределение

где ψ(ax + b), a - параметр масштаба; b - параметр сдвига. Функция ψ(x) удовлетворяет дифференциальному уравнению вида

Логистическое распределение вероятностей близко к их нормальному распределению

где Ф(x) - функция нормального распределения с математическим ожиданием, равным 0, и дисперсией, равной 1. Распределения применяются для аппроксимации результатов теоретических и экспериментальных исследований, полученных при изучении сатурационных процессов с наличием предельного значения функции. Сатурационные процессы описывают: накопление биомассы в зерновке, при ее созревании; рост урожайности, при воздействии определенных факторов; изменение скорости движения хлебной массы в молотильном зазоре; статистические распределения прочности механической связи колосков с плодоножкой; урожайность культур от количества удобрений. Логистические функции являются трехпараметрическими, соответственно не линеаризуются. Многие процессы хорошо описываются логистической функцией при 0 ≤ x ≤ ∞. Предлагаем алгоритм расчета ее параметров. Функция вида

удовлетворяет уравнению

при начальном уравнении ψ(0) = 0,5, тогда функция удовлетворяет уравнению:

, (1)

при условии y(0) = 0 и при x ≥ 0, b > 0, c > 0.

При различных значениях b, c и y_max получим кривые, согласующиеся с экспериментальными данными, которые могут быть представлены в виде:

, (2)

при условии, что b > 0, c > 0.

Значения параметров c и b определяются при y_max.

Путем последовательных преобразований, с подстановкой , получим

(3)

(4)

Рис. 1. Потери зерна от подачи при различных рабочих зазорах

Рис. 2. Зависимость поверхности откликов потерь зерна
от рабочего зазора и производительности молотильно-сепарирующего устройства

Дифференцируя функцию (3) дважды получим:

(5)

Пусть

(6)

где x₀ - абсцисса точки перегиба логисты.

Ордината точки перегиба равна:

(7)

При b → ∞, получим y₀ → 0,5y_max.

Ордината точки перегиба не может быть больше половины ординаты «насыщения»:

y₀ = 0,5y_max. (8)

Из (7) видно, что значение коэффициента b влияет на ординаты точки перегиба.

(9)

На положение абсциссы точки перегиба влияют коэффициенты b и c, т.к. x₀ = lnb/c.

Выражение углового коэффициента касательной в точке перегиба имеет вид:

(10)

Выводы.

1. Получен алгоритм расчета логистических зависимостей потерь зерна при любом распределении массива результатов экспериментальных исследований.

2. Анализ технологических процессов в сельскохозяйственном производстве, показал, что применение логисты при их описании являются более эффективным, чем использование других эмпирических и полуэмпирических зависимостей.

3. При применении логисты имеется возможность изучения процессов в любом интервале изменения аргументов.

ПРИНЦИПЫ И ОСОБЕННОСТИ КАЧЕСТВЕННОГО РАЗВИТИЯ НЕГОСУДАРСТВЕННЫХ ДОШКОЛЬНЫХ ОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЙ

Статья в формате PDF 118 KB...

24 04 2024 21:50:42

ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТОРЦЕВОГО ВЫПУСКА РУДЫ

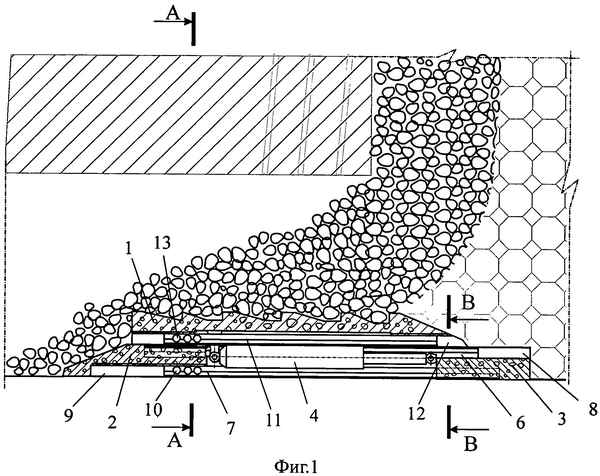Работа посвящена физическому моделированию торцевого выпуска руды при системах с обрушением руды и вмещающих пород. Актуальность темы определяется необходимостью повышения эффективности отработки рудных месторождений полезных ископаемых с применением систем с обрушением. Рассматриваемые системы хаpaктеризуются высокими показателями потерь и разубоживания руды. Моделирование выпуска руды позволят решать вопрос оптимизации параметров системы разработки и совершенствования технологических процессов очистной выемки. ...

23 04 2024 16:36:38

ПРИКЛАДНОЕ ЗНАЧЕНИЕ СРАВНИМОСТИ ЧИСЕЛ В КРИПТОГРАФИИ

Статья в формате PDF 851 KB...

22 04 2024 23:32:17

БЕЗАВТОКЛАВНЫЕ СИЛИКАТНЫЕ ИЗДЕЛИЯ НА ОСНОВЕ МЕСТНЫХ СЫРЬЕВЫХ РЕСУРСОВ И ПРИРОДНЫХ ОТХОДОВ

Статья в формате PDF 121 KB...

21 04 2024 17:16:58

ВЛИЯНИЕ БАКЛОФЕНА НА ПОВЕДЕНИЕ КРЫС С ИММУНОПАТОЛОГИЕЙ

Статья в формате PDF 163 KB...

20 04 2024 8:20:54

БЕНЧМАРКИНГОВЫЙ МЕТОД ОЦЕНКИ КОНКУРЕНТОСПОСОБНОСТИ СПЕЦИАЛИСТОВ

Статья в формате PDF 373 KB...

19 04 2024 9:18:24

Опыт применения и перспективы использования электромагнитного излучения миллиметрового диапазона в терапии больных язвенной болезнью двенадцатиперстной кишки

Статья в формате PDF 109 KB...

18 04 2024 12:31:26

ОСОБЕННОСТИ ТЕХНОЛОГИИ ПРОИЗВОДСТВА КОНЦЕНТРАТА МОЛОЧНОЙ СЫВОРОТКИ

Статья в формате PDF 205 KB...

17 04 2024 20:52:17

АКТИВНОСТЬ АЛЬДЕГИДДЕГИДРОГЕНАЗЫ В ЭРИТРОЦИТАХ, ТРОМБОЦИТАХ И ПЛАЗМЕ КРОВИ КРЫС В НОРМЕ И ПРИ ОЖОГЕ

Статья в формате PDF 116 KB...

16 04 2024 22:27:58

ВОЗМОЖНОСТИ УЛЬТРАЗВУКА В ДИАГНОСТИКЕ ГЛАЗНОГО ИШЕМИЧЕСКОГО СИНДРОМА

Статья в формате PDF 112 KB...

15 04 2024 9:48:26

ВЛИЯНИЕ РАДИАЦИИ НА ПЕРЕКИСНОЕ ОКИСЛЕНИЕ ЛИПИДОВ

Статья в формате PDF 257 KB...

14 04 2024 3:49:44

ИСПОЛЬЗОВАНИЕ ПЕКТИНА С ЦЕЛЬЮ УЛУЧШЕНИЯ КАЧЕСТВА ХЛЕБА

Статья в формате PDF 245 KB...

13 04 2024 1:53:55

К ВОПРОСУ О БИОЛОГИЧЕСКОЙ АКТИВНОСТИ ХРИЗОТИЛ-АСБЕСТА

Статья в формате PDF 119 KB...

12 04 2024 15:39:56

ПРОБИОТИКИ – НОВЫЙ ПОДХОД К СТАРЫМ ПРОБЛЕМАМ

Статья в формате PDF 126 KB...

11 04 2024 6:51:28

ПРОБЛЕМЫ ПРЕПОДАВАНИЯ КУРСА “ВЫСШАЯ МАТЕМАТИКА” НА ЕСТЕСТВЕННОНАУЧНЫХ ФАКУЛЬТЕТАХ

Статья в формате PDF 98 KB...

10 04 2024 5:25:12

К ПРОБЛЕМЕ КАДРОВОГО ОБЕСПЕЧЕНИЯ

В статье рассматривается один из вариантов решения проблемы трудовых ресурсов для России. Эта проблема в силу демографического спада и пpaктиковавшейся не одно десятилетие порочной пpaктики монопсонии¸ как государственной доктрины стала очень острой. Описывается процесс распределения нагрузки в процессе освоения массовых рабочих профессий с учетом психологических и психофизиологических особенностей обучаемого на основе базовой системы микроэлементного нормирования. ...

09 04 2024 9:13:25

ТИПОГРАФИКА (учебное пособие)

Статья в формате PDF 116 KB...

08 04 2024 2:48:55

Максимальная скорость окисления оксида азота

Статья в формате PDF 344 KB...

07 04 2024 15:14:25

ГИГИЕНИЧЕСКОЕ ОБОСНОВАНИЕ БИОЛОГИЧЕСКОЙ ПДК ДИСПЕРСНЫХ АЗОКРАСИТЕЛЕЙ НА ПРИМЕРЕ ЖЕЛТО-КОРИЧНЕВОГО 2Ж И АЛОГО 2А

Статья в формате PDF 303 KB...

06 04 2024 12:34:54

СОЗДАНИЕ ЛЕКАРСТВЕННЫХ ФОРМ ПРОТИВОВОСПАЛИТЕЛЬНОГО ДЕЙСТВИЯ

Статья в формате PDF 135 KB...

05 04 2024 14:27:26

О ПРЕПОДАВАНИИ МАТЕМАТИКИ ДЛЯ ГУМАНИТАРИЕВ

В статье описаны связи между общественными науками и математикой. Приведены рекомендации о преподавании математики для студентов-гуманитариев. Библиогр. 4 назв. ...

04 04 2024 9:12:47

ГОСУДАРСТВЕННЫЙ АНТИМОНОПОЛЬНЫЙ КОНТРОЛЬ ЗА ЭКОНОМИЧЕСКОЙ КОНЦЕНТРАЦИЕЙ КАК ВИД ГОСУДАРСТВЕННОГО КОНТРОЛЯ В РФ

Данная статья является отчетом о научной деятельности, которая была проведена в рамках диссертационного исследования вопросов российского антимонопольного законодательства. В исследовании затронут ряд хаpaктерных правовых проблем, таких как: различные процедуры антимонопольного контроля в России, причины и условия антимонопольного регулирования экономической концентрации и т.д. В ходе исследования и работы по этой теме были изучены научные статьи и публикации других авторов. Полная библиография приведена в конце статьи, некоторые прямые ссылки можно найти в тексте. ...