ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ

равнения существует, когда оно единственно, решается так называемыми теоремами существования и единственности. Эти теоремы очень важны, как для самой теории, так и для пpaктики. Они гарантируют законность применения качественных методов теории дифференциальных уравнений для решения задач естествознания и техники. Численному интегрированию дифференциального уравнения обязательно должно предшествовать обращение к теоремам существования и единственности. И это необходимо делать для того, чтобы избежать недоразумений или вообще неправильных выводов.
Теорема существования. Если в уравнении
(1) функция f определена и непрерывна в некоторой ограниченной области D плоскости (x, y), то для любой точки (x0, y0) € D существует решение y(x) начальной задачи, y(x0) = y0, (2)
определенное на некотором интервале, содержащем точку x0.
Теорема существования и единственности. Если в уравнении функция f определена и непрерывна в некоторой ограниченной области D плоскости (x,y), причем она удовлетворяет в области D условию Липшица по переменной y, т.е.
Теорема о продолжении. При выполнении условий теоремы существования или теоремы существования и единственности всякое решение уравнения с начальными данными (x0, y0) Î D может быть продолжено до точки, сколь угодно близкой к границе области D. При этом в первом случае продолжение, вообще говоря, будет не обязательно единственным, во втором же случае оно единственно.
Для иллюстрации «недоразумений» возникающих при использовании численных решений дифференциальных уравнений без учета теорем существования рассмотрим несколько примеров.
Пример 1. Требуется, используя численный метод интегрирования Эйлера с итерационной схемой
c шагом h =0,1, решить начальную задачу
y(-1) = 0,21 (3)
на отрезке [-1, 3].
Решение. (c помощью пакета Mathcad)
Обратимся теперь к теореме существования. Для исследуемой начальной задачи (3) функция f, определяемая равенством, определена и непрерывна во всей плоскости (x, y) за исключением точек оси абсцисс.
Таким образом, в соответствии с теоремой существования существует решение y(x) начальной задачи (3), определенное на некотором интервале, содержащем точку x0 = -1, и это решение по теореме о продолжении может быть продолжено до значения, близкого к значению y(x) = 0. В результате численного интегрирования получаем решение начальной задачи (3) на некотором интервале (a, b), где a < -1; 1,3 < b < 1,32. Однако, учитывая, что это уравнение с разделяющимися переменными, можно аналитически найти частное решение, удовлетворяющее начальной задаче (3)
Интегрируя, получаем, что
Отсюда следует, что решение начальной задачи (3) существует только для
Оказывается, обращение к теореме существования (и к теореме о продолжении) позволило отсечь отрезок (приблизительно [1,315; 5]), на котором решение исходной начальной задачи (3) заведомо не существует. Одно же только численное интегрирование приводит к ошибочному результату. Дело здесь в том, что при приближении решения y = y(x) к оси Ox угол наклона кривой приближается к 90°. Поэтому пока аргумент x изменяется на величину 0,1 значение y успевает перескочить ось Ox, и мы попадаем на интегральную кривую, отличную от исходной. А это происходит потому, что метод Эйлера учитывает угол наклона только в текущей точке.
Пример 2. Используя метод Эйлера, а затем метод Эйлера-Коши, с шагом h = 0,1 и итерационной схемой
,
где
,
решить начальную задачу
y(-1) = -1, (4)
на промежутке [-1, 1].
Решение. На базе Mathcad методом Эйлера, а затем методом Эйлера-Коши будем иметь:
Рис. 2
Получили чертеж (рис. 3) отличный от чертежа, изображенного на (рис. 2). Чтобы лучше разобраться в причине расхождения в результатах, проинтегрируем исходную начальную задачу. Разделяя переменные, имеем
или, окончательно, .
Становится понятно, что решение по методу Эйлера приближает функцию y1(x) = x3, а по улучшенному методу Эйлера - функцию
При этом как, y1 так и y2 являются решениями начальной задачи (4), а значит, для рассматриваемой на промежутке [-1; 1] начальной задачи имеет место неединственность.
Обращаясь теперь к теореме существования и единственности, отметим, что, так как функция f, заданная равенством, непрерывна во всей плоскости (x, y), то из теоремы существования следует, что существует решение начальной задачи (4), определенное на некотором промежутке, содержащем точку x0 = -1, и это решение по теореме о продолжении может быть продолжено на любой промежуток. Далее, поскольку
,
то функция
удовлетворяет условию Липшица по переменной y в любой области, не содержащей точки оси Ox. Если же область содержит точку оси Ox, то нетрудно показать, что в ней указанная выше функция условию Липшица не удовлетворяет. Поэтому из теоремы существования и единственности (и теоремы о продолжении) следует, что в данном случае решение начальной задачи может быть продолжено единственным образом, по крайней мере, до оси Ox. Но поскольку прямая y = 0 является особой интегральной прямой для дифференциального уравнения
,
то, как только y станет равным нулю решение начальной задачи (4) не может быть единственным образом продолжено за точку O(0, 0).
Рис. 3
Итак, обращение в данном случае к теореме существования и единственности (и теореме о продолжении) позволило разобраться в результатах численного интегрирования. Если речь идет о единственном на промежутке [-1; 1] решении начальной задачи (4), то оно существует и определено лишь на отрезке [-1; 0]. В общем же случае таких решений несколько.
Список литературы
1. Roberts C.E. Jr. Why teach existence and uniqueness theorems in the first course in ordinary differential equations? // Int. J. Math. Educ. Sci. Technol. - 1976. - Vol. 7, № 1. - P. 41-44.
19 04 2024 4:48:46
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
18 04 2024 11:21:35
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
17 04 2024 14:33:25
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
16 04 2024 10:19:12
 Статья в формате PDF
262 KB...
Статья в формате PDF
262 KB...
15 04 2024 4:54:17
 Статья в формате PDF
498 KB...
Статья в формате PDF
498 KB...
14 04 2024 4:33:14
 Статья в формате PDF
269 KB...
Статья в формате PDF
269 KB...
12 04 2024 21:41:46
 Статья в формате PDF
304 KB...
Статья в формате PDF
304 KB...
11 04 2024 7:37:10
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
10 04 2024 19:49:18
 Статья в формате PDF
786 KB...
Статья в формате PDF
786 KB...
09 04 2024 22:17:55
 Статья в формате PDF
130 KB...
Статья в формате PDF
130 KB...
08 04 2024 21:41:36
 Статья в формате PDF
293 KB...
Статья в формате PDF
293 KB...
07 04 2024 7:13:40
 Статья в формате PDF
309 KB...
Статья в формате PDF
309 KB...
06 04 2024 15:24:20
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
05 04 2024 14:35:44
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
04 04 2024 7:40:39
 Статья в формате PDF
311 KB...
Статья в формате PDF
311 KB...
03 04 2024 0:41:18
02 04 2024 12:43:56
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
01 04 2024 22:26:45
 Статья в формате PDF
215 KB...
Статья в формате PDF
215 KB...
31 03 2024 22:59:20
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
30 03 2024 10:37:42
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
29 03 2024 16:56:35
 Статья в формате PDF
379 KB...
Статья в формате PDF
379 KB...
28 03 2024 12:22:10
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
27 03 2024 21:36:23
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
26 03 2024 9:24:40
 Статья в формате PDF
153 KB...
Статья в формате PDF
153 KB...
25 03 2024 8:19:27
 Предпосылками для использования лигандов соматостатиновых рецепторов в гастроэнтерологии являются существующие представления о биологических и фармакологических эффектах соматостатина и его аналогов. Нейропептид и его аналоги индуцируют ряд физиологических реакций и в их числе эффект угнетения панкреатической секреции. Соматостатин и октреотид могут модулировать продукцию цитокинов, снижать влияние токсинов на клетки печени, желудка и панкреатические ациноциты, влиять на панкреатический кровоток. Неодинаковый хаpaктер лиганд-рецепторного взаимодействия соматостатина и октреотида с разными подтипами SST-рецепторов обуславливают различия их биологических эффектов.
...
Предпосылками для использования лигандов соматостатиновых рецепторов в гастроэнтерологии являются существующие представления о биологических и фармакологических эффектах соматостатина и его аналогов. Нейропептид и его аналоги индуцируют ряд физиологических реакций и в их числе эффект угнетения панкреатической секреции. Соматостатин и октреотид могут модулировать продукцию цитокинов, снижать влияние токсинов на клетки печени, желудка и панкреатические ациноциты, влиять на панкреатический кровоток. Неодинаковый хаpaктер лиганд-рецепторного взаимодействия соматостатина и октреотида с разными подтипами SST-рецепторов обуславливают различия их биологических эффектов.
...
24 03 2024 12:34:20
23 03 2024 23:28:59
 Статья в формате PDF
250 KB...
Статья в формате PDF
250 KB...
22 03 2024 7:50:50
 Статья в формате PDF
414 KB...
Статья в формате PDF
414 KB...
21 03 2024 5:57:45
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
19 03 2024 6:42:31
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
17 03 2024 1:11:24
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
16 03 2024 8:42:15
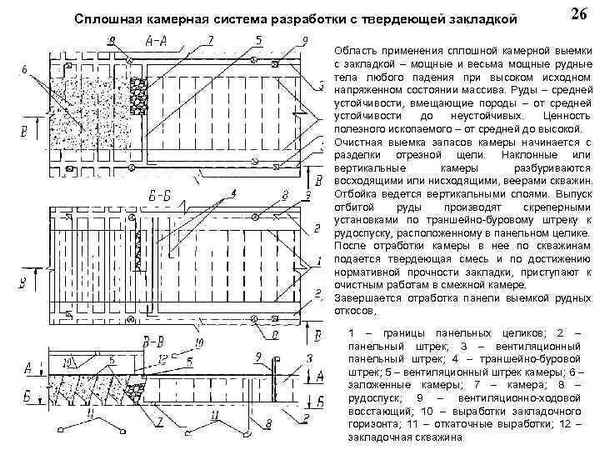
 В данной работе приводятся результаты экологических исследований по состояния северных экосистем, с целью разработки возможных мероприятий по снижению негативных воздействий на окружающую среду при горно-добычных работах открытых карьерным способом. Выявлены закономерности приуроченности накопления тяжелых металлов на определенных типах почв.
...
В данной работе приводятся результаты экологических исследований по состояния северных экосистем, с целью разработки возможных мероприятий по снижению негативных воздействий на окружающую среду при горно-добычных работах открытых карьерным способом. Выявлены закономерности приуроченности накопления тяжелых металлов на определенных типах почв.
...
15 03 2024 11:23:23
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
14 03 2024 16:49:39
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::