Асимптотика решений дифференциального уравнения четвёртого порядка с запаздывающим аргументом (с суммируемым потенциалом)
Рассмотрим дифференциальное уравнение четвёртого порядка:
(1)
с начальным условием
(2)
где τ - запаздывание; λ - спектральный параметр; ρ(x) = a4 - весовая функция, причём предполагается, что потенциал q(x) и начальная функция φ(x) - суммируемые функции на отрезке [0; π]:
Пусть
.
Пусть
.Теорема 1. Решение y(x, s) дифференциального уравнения (1)-(2) является решением следующего интегрального уравнения Вольтерра:
(3)
Теорема 2. Общее решение дифференциального уравнения (1)-(2) имеет следующий вид:
(4)
если
Аналогично получаются асимптотические формулы при и
Метод доказательства теорем 1 и 2 изложен автором в работе [1].
Список литературы
1. Митрохин С.И. Асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами // Вестник Московского ун-та. Сер.1, математика, механика. - 2009. - №3 - С. 14-17.
Статья в формате PDF
108 KB...
19 04 2024 21:27:31
Статья в формате PDF
115 KB...
18 04 2024 7:34:36
Статья в формате PDF
114 KB...
17 04 2024 4:22:58
Статья в формате PDF
108 KB...
15 04 2024 18:30:33
Статья в формате PDF
329 KB...
14 04 2024 16:32:43
Статья в формате PDF
327 KB...
12 04 2024 13:51:42
Статья в формате PDF
280 KB...
11 04 2024 1:26:46
В статье раскрываются адаптационная деятельность организма, показано, что функциональная система регуляции кровообращения представляет собой многоконтурную, иерархически организованную систему, в которой доминирующая роль отдельных звеньев определяется текущими потребностями организма.
...
10 04 2024 18:57:43
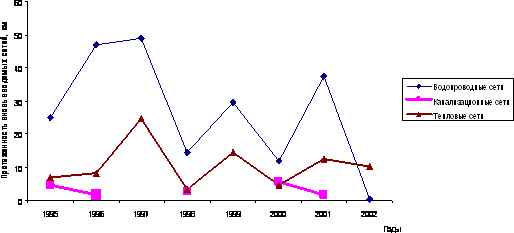В статье дается хаpaктеристика современного состояния жилищно-коммунального хозяйства Саратовской области. Отмечаются изменения в структуре собственности на жилищный фонд, оцениваются тенденции развития основных фондов жилищно-коммунального хозяйства, состояние кадров и платежно-расчетной дисциплины в отрасли, освещается политика администрации области в части организационных преобразований системы управления жилищно-коммунальным хозяйством и обеспечения социальных гарантий для населения.
...
09 04 2024 11:59:49
Статья в формате PDF
98 KB...
08 04 2024 16:43:26
Статья в формате PDF
107 KB...
07 04 2024 22:57:21
Статья в формате PDF
111 KB...
06 04 2024 3:57:18
Статья в формате PDF
243 KB...
05 04 2024 3:26:53
Статья в формате PDF
108 KB...
03 04 2024 17:21:10
Статья в формате PDF
87 KB...
02 04 2024 21:20:19
Статья в формате PDF
115 KB...
31 03 2024 11:28:56
Статья в формате PDF
245 KB...
30 03 2024 13:19:22
Статья в формате PDF
107 KB...
29 03 2024 5:18:29
Статья в формате PDF
101 KB...
28 03 2024 17:17:39
Статья в формате PDF
307 KB...
26 03 2024 8:56:53
Статья в формате PDF
81 KB...
23 03 2024 16:55:42
Статья в формате PDF
110 KB...
22 03 2024 21:26:52
Статья в формате PDF
118 KB...
21 03 2024 23:51:21
С целью уточнения хаpaктера иммунопатологического процесса при псориатической болезни и выяснения аутоиммунного механизма воспаления авторами проведено клинико-иммунологическое обследование 132 больных псориатической болезнью. Комплексное иммунологическое обследование пациентов с определением содержания органоспецифических и органонеспецифических аутоантител к различным тканевым и органным антигенам позволило определить аутоиммунный тип иммунной патологии как один из ведущих механизмов воспаления при данной патологии.
...
20 03 2024 5:52:39
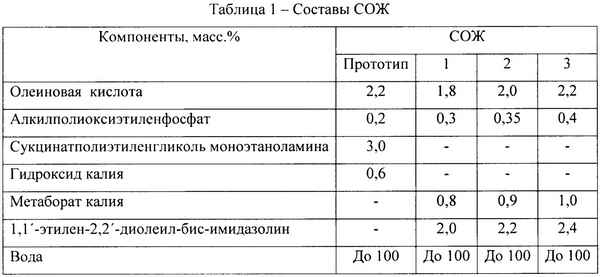Статья в формате PDF
100 KB...
19 03 2024 7:28:47
Статья в формате PDF
250 KB...
18 03 2024 0:53:49
Статья в формате PDF
89 KB...
17 03 2024 9:11:55
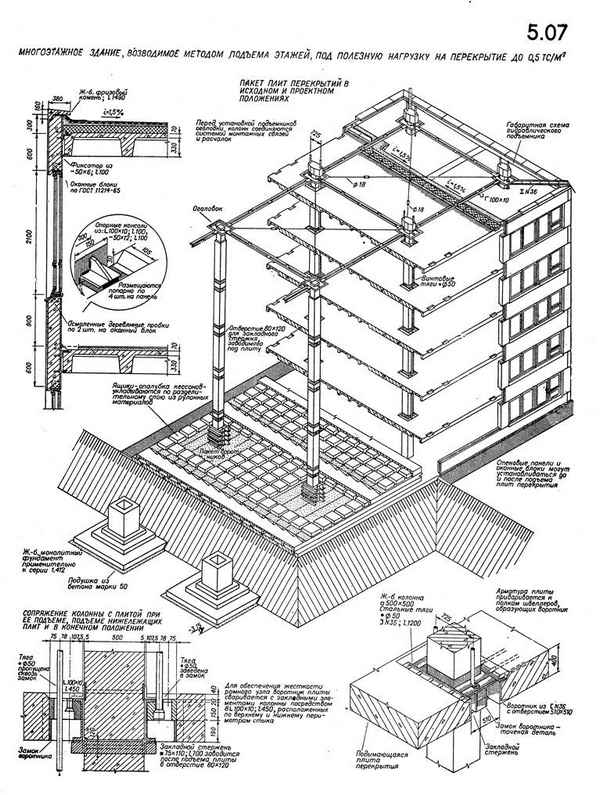Статья в формате PDF
349 KB...
16 03 2024 17:56:30
Статья в формате PDF
326 KB...
15 03 2024 22:31:42
Статья в формате PDF
345 KB...
14 03 2024 18:14:22
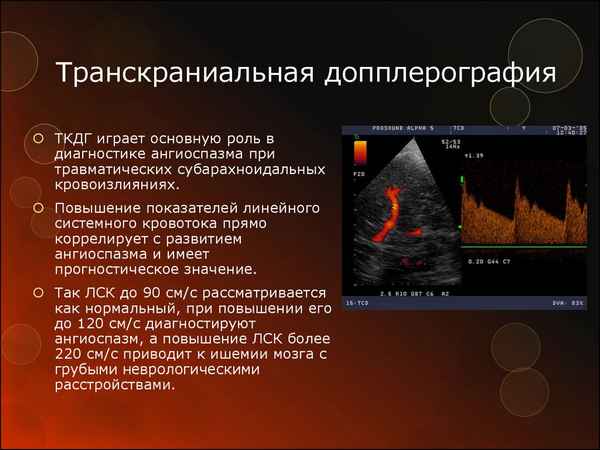Статья в формате PDF
107 KB...
13 03 2024 14:42:28
Статья в формате PDF
305 KB...
12 03 2024 2:20:25
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
