К ПРОБЛЕМЕ ПОСТРОЕНИЯ ОПЕРАТОРНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ ДЛЯ 2D СИСТЕМ

1. В работе выводятся операторные и интегральные уравнения движения 2D систем. Рассмотрим два семейство взаимно перпендикулярных упругих одинаковых линейных струн, защемленных на концах и имеющих соответственно длины L1 и L2. Каждая струна нумеруется при помощи индексов k = 0,1,2,., N1 и q = 0,1,2.. N2. Пусть струны образуют решетчатую 2D систему. В точках сопряжения помещены абсолютно твердые тела массами m. Главная особенность системы - ее состояние дается матрицей прогибов объекта в узлах.
Предположения: прямоугольные ячейки одинаковы; решетка - анизотропна; струнные элементы - безынерционны. Пусть силы диссипации, вынуждающие силы, а также любые другие неконсервативные силы - малы. Обозначив их εgkq(t, ukq, kq,...), ε - малый параметр. Так как каждая частица лежит одновременно на двух струнах, то для всех значений индексов имеем
N уравнений [N= (N1 -1)(N2-1)]:
m kq+c1(2ukq-u(k-1,q)- u(k+1,q))+c2(2ukq-u(k,q-1)- u(k,q+1))= εgkq(t, ukq, kq,...), (1)
где: с1,2 - коэффициенты упругости. Граничные условия: ukq=0, при k=0;N1; q=0;N2.
2. Приведем операторные уравнения движения, следующие из уравнений (1). В соответствии с общими методиками [1, 2,] построим оператор динамической податливости:
,
В данном случае выражение Lkq,nj(p) обозначает проходной оператор [1], ставящей в соответствие силе, приложенной в узле (n,j) перемещение узла (k,q). При n=k, j=q - имеем локальные операторы динамической податливости [2], отвечающие перемещению узла, вследствие силы, приложенной в нем самом. Для рассматриваемой системы принцип взаимности записывается как Lkq,nj(p) == Lnj,kq (p).
Система уравнений движения (1) при этом разрешается в виде:
где ε||gkq|| - матрица внешних сил, приложенных в узлах решетки, что покомпонентно записывается так:
(2)
Выражения для операторов динамических податливостей полностью определяются наборами собственных частот {Ωkq} и нормированных коэффициентов собственных форм.
{Θkq} линейной системы [2].Используя результаты, данные в монографии [1] для решетки рассматриваемого типа:
С=const. При этом в силу выбранных граничных условий n = 1,2,... N1-1 и также j = 1,2,... N2-1. В соответствии с методами построения операторов динамической податливости [2] можно получить для компонентов оператора (p), определяющих (2):
. (5)
Здесь введен нормировочный коэффициент ζ , который, в общих случаях удобнее всего вычислять при конкретно заданных параметрах системы. В данном случае можно положить: ζ=2[(N1-1)(N2-1)]-2.
3. Операторное представление (2) - универсально. Внося конкретизирующие предположения, можно получить простые представления для реализации формулы (2).
Если правые части (1) периодичны по времени с периодом Т: при всех k и q,то. отыскивая Т - периодическое решение, можно воспользоваться методами интегральных представлений периодических решений [2]:
(5)
где функции Χkq,nj(t-s) называются Т - периодическими функциями Грина (ПФГ) [2-4] - проходными (k¹n; q¹j) или локальными (k=n; q=j) и определяются соответствующим оператором динамической податливости так (T=2πω-1):
ПФГ Χkq,nj (t) - реакция узла (k,q) на силовое воздействие, приложенное в узле (n,j) и описываемое Т - периодической последовательностью δ-функций Диpaка - δT(t): определению
Эту обобщенную функцию можно разложить в сходящийся в обобщенном смысле ряд Фурье вида:
Работа выполнена при поддержке РФФИ (Проект 05-08-50183).
СПИСОК ЛИТЕРАТУРЫ:
- Нагаев Р.Ф., Ходжаев К.Ш. Колебания механических систем с периодической структурой. - Ташкент: ФАН, 1973. - 272 с.
- Бабицкий В.И., Крупенин В.Л. Колебания в сильно нелинейных системах. - М., Наука, 1985. - 384 с.
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
26 04 2024 3:40:58
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
25 04 2024 17:52:49
Статья в формате PDF 235 KB...
23 04 2024 14:37:19
 Статья в формате PDF
146 KB...
Статья в формате PDF
146 KB...
22 04 2024 17:43:54
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
21 04 2024 16:22:41
 Статья в формате PDF
236 KB...
Статья в формате PDF
236 KB...
19 04 2024 7:36:43
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
18 04 2024 11:30:43
 Статья в формате PDF
136 KB...
Статья в формате PDF
136 KB...
16 04 2024 16:19:23
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
15 04 2024 20:42:50
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
14 04 2024 18:15:29
 Статья в формате PDF
249 KB...
Статья в формате PDF
249 KB...
12 04 2024 1:32:45
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
10 04 2024 19:49:19
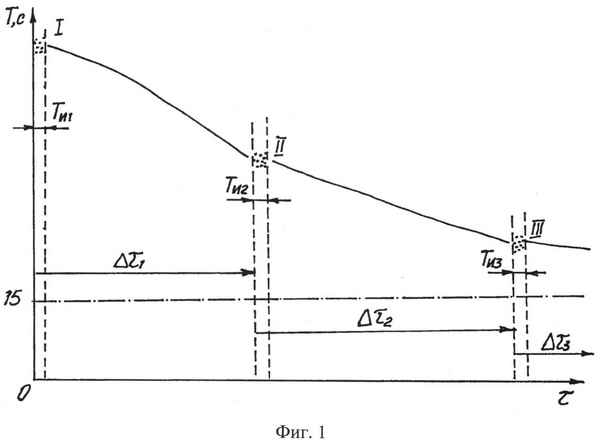 Летом 2012 года был проведен мониторинг расхода воды на малом водотоке. Мерный сосуд был принят в виде ковша емкостью один литр. Все измерения проводились вечером с 17-00 часов. Поэтому текущее время берется целыми сутками. Модель динамики имеет две составляющие: первая составляющая является законом экспоненциального роста, а вторая волновым возмущением с переменными амплитудой и частотой колебания. Показана методика моделирования с процеДypaми: 1) выявление постоянного члeна; 2) по остаткам от постоянного члeна, последовательно усложняя конструкцию, идентифицируется волновая функция; 3) постоянный члeн совмещается с волновой функцией; 4) усложняется конструкция тренда до устойчивого не волнового закона.
...
Летом 2012 года был проведен мониторинг расхода воды на малом водотоке. Мерный сосуд был принят в виде ковша емкостью один литр. Все измерения проводились вечером с 17-00 часов. Поэтому текущее время берется целыми сутками. Модель динамики имеет две составляющие: первая составляющая является законом экспоненциального роста, а вторая волновым возмущением с переменными амплитудой и частотой колебания. Показана методика моделирования с процеДypaми: 1) выявление постоянного члeна; 2) по остаткам от постоянного члeна, последовательно усложняя конструкцию, идентифицируется волновая функция; 3) постоянный члeн совмещается с волновой функцией; 4) усложняется конструкция тренда до устойчивого не волнового закона.
...
09 04 2024 9:13:16
 Статья в формате PDF
474 KB...
Статья в формате PDF
474 KB...
08 04 2024 0:13:43
 В статье изложены результаты тестирования ориентировочно-исследовательского поведения крыс указанных линий, которые показали, что крысы линии WAG/Rij обладают более выраженной двигательной активностью и исследовательской деятельностью по сравнению с крысами линии Вистар.
...
В статье изложены результаты тестирования ориентировочно-исследовательского поведения крыс указанных линий, которые показали, что крысы линии WAG/Rij обладают более выраженной двигательной активностью и исследовательской деятельностью по сравнению с крысами линии Вистар.
...
07 04 2024 8:59:30
 Статья в формате PDF
276 KB...
Статья в формате PDF
276 KB...
03 04 2024 10:40:19
 Статья в формате PDF
295 KB...
Статья в формате PDF
295 KB...
02 04 2024 23:42:17
 Статья в формате PDF
263 KB...
Статья в формате PDF
263 KB...
01 04 2024 18:11:36
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
31 03 2024 18:26:27
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
29 03 2024 5:45:27
 Статья в формате PDF
150 KB...
Статья в формате PDF
150 KB...
28 03 2024 5:51:24
 Анализ опыта по восстановлению методом агростепей растительности на нарушенных кормовых угодьях долины средней Лены показал, что метод при соблюдении экологических условий и видового состава участков обеспечивает восстановление растительности, проявляющееся в повышении проективного покрытия и доминировании в травостое целинных видов. Соответствие экологических условий и видового состава травостоя при подборе участков обеспечивает восстановление растительности нарушенных участков до 70–75 % и доминирование в травостое целинных видов до 60–65 % в условиях нормального и сильного засоления.
...
Анализ опыта по восстановлению методом агростепей растительности на нарушенных кормовых угодьях долины средней Лены показал, что метод при соблюдении экологических условий и видового состава участков обеспечивает восстановление растительности, проявляющееся в повышении проективного покрытия и доминировании в травостое целинных видов. Соответствие экологических условий и видового состава травостоя при подборе участков обеспечивает восстановление растительности нарушенных участков до 70–75 % и доминирование в травостое целинных видов до 60–65 % в условиях нормального и сильного засоления.
...
27 03 2024 8:21:47
 Механизмы «хаотической» составляющей в динамике сердечного ритма недостаточно еще ясны и была предпринята попытка выявить их на основе совместного анализа линейных и нелинейных показателей. Показано, что коэффициент корреляции между этими показателями не превышает 0,5. Высказано предположение, что нерегулярные изменения сердечного ритма являются проявлением избирательного усиления одних и подавления других периодических процессов в динамике кардиоритма, как результат различных регуляторных влияний.
...
Механизмы «хаотической» составляющей в динамике сердечного ритма недостаточно еще ясны и была предпринята попытка выявить их на основе совместного анализа линейных и нелинейных показателей. Показано, что коэффициент корреляции между этими показателями не превышает 0,5. Высказано предположение, что нерегулярные изменения сердечного ритма являются проявлением избирательного усиления одних и подавления других периодических процессов в динамике кардиоритма, как результат различных регуляторных влияний.
...
26 03 2024 1:39:37
 Статья в формате PDF
286 KB...
Статья в формате PDF
286 KB...
25 03 2024 5:19:17
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
24 03 2024 16:34:32
 Статья в формате PDF
284 KB...
Статья в формате PDF
284 KB...
22 03 2024 9:17:22
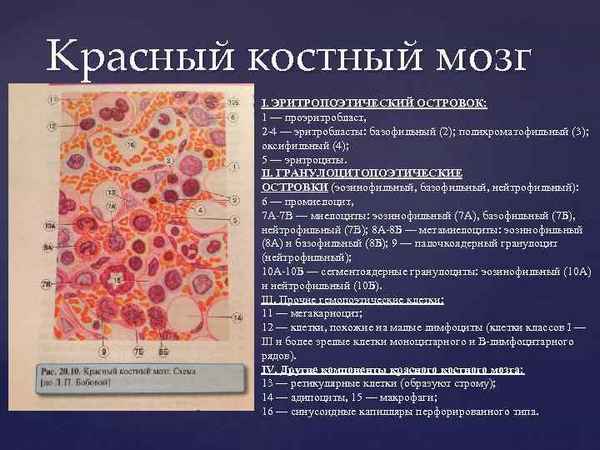 Проведено исследование хаpaктера образования эритроклазических костномозговых кластеров при лихорадке у лабораторных животных. Установлено, что лихорадка сопровождается увеличением клеточности костного мозга, активацией эритроклазического кластерообразования нейтрофильными миелокариоцитами и макрофагами, сопровождающегося усилением экзоцитарного лизиса эритроцитов в кластерах, то есть увеличением цитолитической активности данных миелокариоцитов.
...
Проведено исследование хаpaктера образования эритроклазических костномозговых кластеров при лихорадке у лабораторных животных. Установлено, что лихорадка сопровождается увеличением клеточности костного мозга, активацией эритроклазического кластерообразования нейтрофильными миелокариоцитами и макрофагами, сопровождающегося усилением экзоцитарного лизиса эритроцитов в кластерах, то есть увеличением цитолитической активности данных миелокариоцитов.
...
21 03 2024 11:18:54
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
20 03 2024 12:45:58
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
19 03 2024 10:57:17
 Статья в формате PDF
401 KB...
Статья в формате PDF
401 KB...
18 03 2024 6:37:14
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::