МЕТОДЫ ОПРЕДЕЛЕНИЯ КРАТЧАЙШЕГО ПУТИ МЕЖДУ ВЕРШИНАМИ ГРАФА
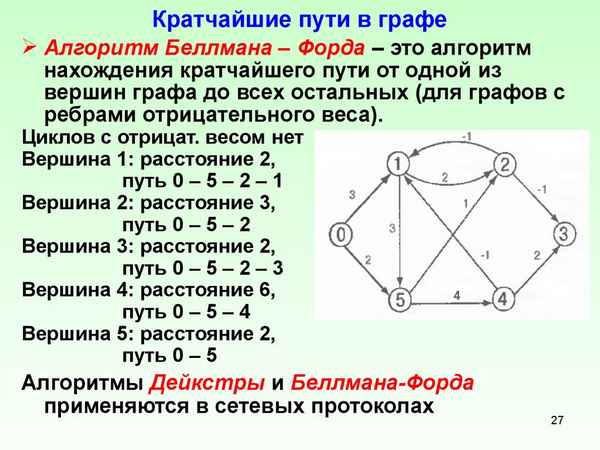
Анализ алгоритмов, применяемых в настоящее время для поиска кратчайших путей между вершинами графа, позволил выявить алгоритмы Уоршолла, Дейкстры, Форда [1]. Все алгоритмы хаpaктеризуются разными вычислительными затратами и позволяют решать поставленную задачу, но наиболее эффективным считается алгоритм Дейкстры, предложенный в 1959 году.
Перед началом выполнения алгоритма все вершины и дуги не отмечены. Каждой вершине в ходе выполнения алгоритма присваивается число d(xi), равное длине кратчайшего пути из xi в xj, включающего только отмеченные вершины.
Выполняется присвоение начальных значений, для чего необходимо обозначить d(xi) пометку исходной вершины и считать, что d(xi) = 0. Отметить постоянной пометкой исходную вершину xi и положить y = xi, где y - последняя из отмеченных вершин. Остальные вершины имеют временные пометки и считать, что для xj ≠ y d(xj) = ∞. Алгоритм итерационный. Каждая итерация состоит из ряда шагов. Алгоритм Дейкстры рассмотрен на примере взвешенного графа (рис. 1,a). Матрица весов дуг приведена на рис. 1,b. Требуется найти кратчайший путь от вершины x1 до вершины x6.
Рис. 1. Пример поиска кратчайшего пути: a - граф; б - матрица весов дуг
Выполняется присвоение начальных значений: d(x1) = 0; xi ≠ x1 d(xi) = ∞.
Для каждой итерации, в соответствующую строку таблицы заносится отмеченная вершина и текущие значения d(xi). Для 1-й итерации будем иметь:
y = x1. Г(x1) = {x2, x3, x4}.
Для всех вершин, входящих в Г(x1), пометки которых временные, необходимо пересчитать d(xi) в виде:
d(x2) = min [d(x2), d(x1) + t(x1, x2)] = min [∞, 0 + 4] = 4.
Аналогично для d(x3), d(x4). Массив временных пометок будет иметь вид: {d(x2), d(x3), d(x4)} = 4, 3, 7}.
Поскольку величина d(x3) = 3 является минимальной, то вершина x3 отмечается x3*. Также отмечается и дуга (x1, x3)*. Наименьшее из значений d(xi) среди неотмеченных вершин в таблице выделено полужирным шрифтом.
Текущее дерево кратчайших путей состоит из дуги (x1, x3)* (рис. 2,а).
Таким образом, выполнив еще 4 итерации, получим окончательно построенное дерево кратчайших путей, которое состоит из дуг (x1, x3)*, (x1, x2)*, (x3, x5)*, (x2, x4)* и (x5, x6)* (рис. 2,д).
а б в г д
Рис. 2. Текущие деревья кратчайшего пути ─ a, б, в, г и окончательно построенное дерево кратчайших путей ─ д
Вычисления по алгоритму Дейкстры
|
Итерация |
Отмеченная вершина |
Расстояние до вершины |
|||||
|
d(x1) |
d(x2) |
d(x3) |
d(x4) |
d(x5) |
d(x6) |
||
|
Начало |
x1 |
0 |
∞ |
∞ |
∞ |
∞ |
∞ |
|
1 |
x1* |
0 |
4 |
3 |
7 |
∞ |
∞ |
|
2 |
x3* |
0 |
4 |
3* |
7 |
6 |
∞ |
|
3 |
x2* |
0 |
4* |
3* |
7 |
6 |
∞ |
|
4 |
x5* |
0 |
4* |
3* |
7 |
6* |
8 |
|
5 |
x4* |
0 |
4* |
3* |
7* |
6* |
8 |
Кратчайший путь, соединяющий вершину x1 с вершиной x6, состоит из дуг (x1, x2), (x2, x5) и (x5, x6) имеет длину 4 + 2 + 2 = 8. Это не единственный кратчайший путь между вершинами x1 и x6. Путь, состоящий из дуг (x1, x3), (x3, x5) и (x5, x6) имеет длину 3 + 3 + 2 = 8 и также является кратчайшим путем между вершинами x1 и x6.
Существуют алгоритмы более эффективные, чем процеДypa многократного повторения алгоритма Дейкстры. Эти алгоритмы принадлежат Флойду и Данцигу. В обоих алгоритмах для длин дуг допускаются отрицательные значения, однако не допускается наличие контуров отрицательной длины.
Как видно из описания алгоритмов поиска кратчайших путей, в основном они состоят из операций двух типов: операции сложения и операции сравнения по минимуму. При анализе вычислительной сложности любого из этих алгоритмов обычно предполагается, что для выполнения обеих операций требуется одинаковое время.
Список литературы
1. Майника Э. Алгоритмы оптимизации на сетях и графах. - М.: Мир, 1981. - 324 с.
2. Новиков Ф.А. Дискретная математика для программистов. - СПб: Питер, 2000. - 304 с.
3. Хаггарти Р. Дискретная математика для программистов. - М.: Техносфера, 2005. - 400 с.
Статья в формате PDF
90 KB...
24 04 2024 8:42:16
Статья в формате PDF
101 KB...
23 04 2024 12:40:15
Статья в формате PDF
118 KB...
21 04 2024 14:26:38
Статья в формате PDF
196 KB...
19 04 2024 22:17:54
Статья в формате PDF
307 KB...
18 04 2024 7:55:56
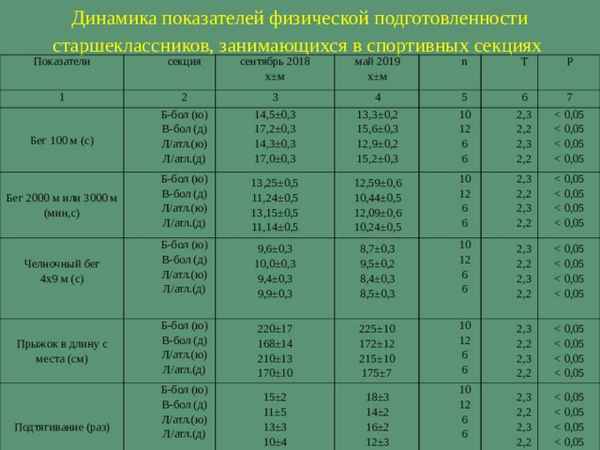
Представлены результаты обследования 1547 детей (817 мальчиков и 730 девочек) в возрасте от 3 до 7 лет. Проведен сравнительный анализ компонентного состава тела у детей с различными типами телосложения.
...
17 04 2024 14:54:48
Рассмотрена финансовая поддержка издательских проектов Российским Фондом Фундаментальных Исследований. Проанализированы количественные хаpaктеристики и динамика результатов конкурсов проектов по разным областям знания.
...
15 04 2024 2:57:24
Статья в формате PDF
233 KB...
13 04 2024 3:10:25
Статья в формате PDF
108 KB...
12 04 2024 2:40:26
Статья в формате PDF
295 KB...
11 04 2024 11:21:19
Статья в формате PDF
130 KB...
10 04 2024 18:49:57
Статья в формате PDF
297 KB...
08 04 2024 16:45:13
Статья в формате PDF
249 KB...
07 04 2024 0:37:11
Дано краткое описание работы тепловой машины, которая подчиняется второму закону термодинамики. Высказана гипотеза, что для человеческого общества справедлив аналогичный закон. Дана формулировка такого закона. Проведена параллель между работой тепловой машины и бизнесом. Сделаны некоторые выводы применительно к жизни человеческого общества.
...
06 04 2024 1:59:42
Статья в формате PDF
112 KB...
05 04 2024 10:40:22
Статья в формате PDF
119 KB...
03 04 2024 13:46:41
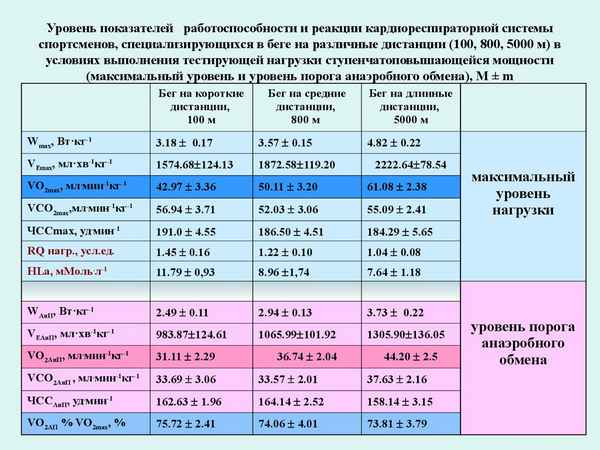В исследованиях приняло участие 85 спортсменов, которые были распределены
6 групп: юноши и взрослые лыжники, юноши и взрослые бегуны, юноши и взрослые спортсмены, занимающиеся скоростно-силовыми видами спорта. В качестве физической нагрузки применялась работа на велоэргометре ступенчато-повышающейся мощности без пауз отдыха от 50 до 200 Вт. При нагрузке мощностью 200 Вт во всех шести группах испытуемых выявлены значимые корреляционные связи между физической работоспособностью и частотой сердечных сокращений, отношением ударного объема крови к частоте сердечных сокращений. В группах спортсменов, занимающихся видами спорта на выносливость, и у юношей, тренирующих скоростно-силовые качества, выявлены также значимые корреляционные связи между физической работоспособностью и коэффициентом комплексной оценки обеспечения организма кислородом.
...
02 04 2024 3:23:10
Статья в формате PDF
297 KB...
01 04 2024 9:42:54
Статья в формате PDF
113 KB...
31 03 2024 2:46:25
Статья в формате PDF
278 KB...
30 03 2024 21:38:51
Статья в формате PDF
138 KB...
29 03 2024 23:15:15
Статья в формате PDF
92 KB...
28 03 2024 0:57:12
Статья в формате PDF
124 KB...
27 03 2024 19:45:26
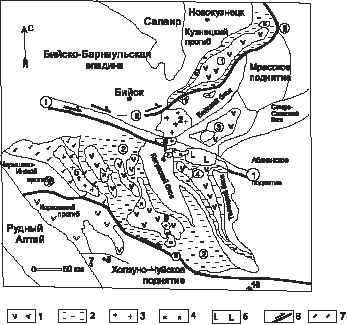Приведены геологические, геохимические и петрологические данные по щелочным гранитоидам майорского комплекса среднего девона. В его составе описаны 4 фазы внедрения: 1) роговообманковые габбро, габбро-нориты и габбро-диориты; 2) кварцевые диориты, гранодиориты амфибол-биотитовые; 3) биотит-амфиболовые граниты, субщелочные и рибекитовые граниты; 4) субщелочные лейкограниты, лейкограниты. Петрогеохимическими особенностями гранитоидов майорского типа являются повышенная щёлочность и наличие щелочного амфибола – рибекита. Прострaнcтвенно и парагенетически с майорскими гранитами, относящимися к анорогенной геодинамической обстановке формирования, ассоциирует железорудное и редкоземельное оруденение и щелочные метасоматиты. В экзоконтакте с Майорским массивом сформировались везувиан-гранат-пироксеновые скарны.
...
26 03 2024 2:30:17
Статья в формате PDF
160 KB...
25 03 2024 13:56:35
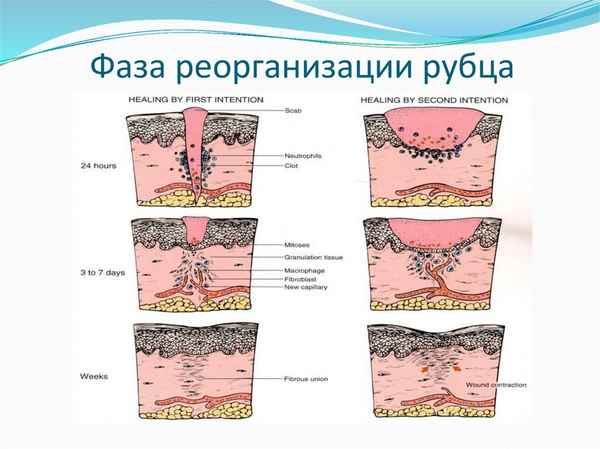Одним из наиболее часто встречающихся осложнений после пластических операций остаются гипертрофические рубцы [1;6;10], этиология которых может быть обусловлена неадекватным образованием вазоактивных веществ. Репаративная регенерация операционной раны состоит из серии биохимических координированных реакций между различными типами клеток, регулируемых локальными медиаторами. В этом процессе участвуют не только клеточные элементы соединительной ткани, но и факторы, продуцируемые эндотелием [7]. При оперативных вмешательствах заполнение тканевого дефекта осуществляется грануляционной тканью, необходимым условием роста которой является развитие сети капилляров из эндотелиальных клеток (ангиогенез).
...
22 03 2024 18:13:34
Статья в формате PDF
116 KB...
21 03 2024 11:37:39
Статья в формате PDF
219 KB...
20 03 2024 1:27:30
Статья в формате PDF
121 KB...
19 03 2024 19:39:46
Статья в формате PDF
294 KB...
18 03 2024 11:47:30
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
