Об устойчивости стационарных режимов в реакторе с кипящим слоем катализатора
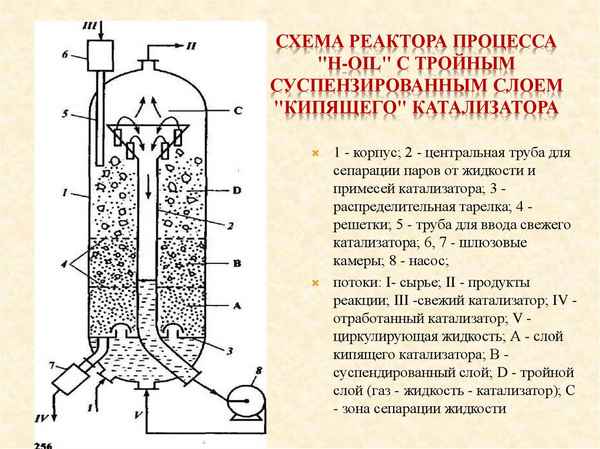
Моделирование процессов в химических реакторах в ряде случаев приводит к краевым задачам для гиперболических уравнений [1-5]. В частности, процесс в реакторе с кипящим слоем катализатора при реакции первого порядка (скорость реакции линейно зависит от концентрации реагирующего вещества) моделируется [1] смешанной задачей для почти линейной гиперболической системы на плоскости
Здесь П - полуполоса (0,1) (0, ∞),θ, θr - температура в реакторе и холодильнике, Ñ - концентрация реагирующего вещества, α, β, γ, δ, θ0 - постоянные, из них первые четыре положительны, начальные функции – гладкие и удовлетворяют условиям согласования нулевого и первого порядков.
В данной работе установлено прямым методом Ляпунова достаточное условие экспоненциальной устойчивости в L2 - норме стационарного решения задачи (1) (вариант этого метода применительно к указанному классу краевых задач предложен в [5]), предварительно получено достаточное условие существования таких решений.
Теорема 1. Для существования хотя бы одного стационарного решения краевой задачи (1) достаточно выполнение неравенства
Пусть выполнено условие (2) и 12 ( z, v1,v2) - стационарное решение краевой задачи (1). Введем вектор отклонений
u = (C-z, θ - v1, θ - v2)
Будем говорить, что стационарное решение задачи (1) экспоненциально устойчиво в L2 - норме, если существует такое δ > 0 , что для решений (C, θ, θr) задачи (1) таких, что |u (x ,0)| < δ при x € при [0,1] , выполняется оценка
Теорема 2. Для экспоненциальной устойчивости в L2 - норме стационарного решения краевой задачи (1) достаточно выполнение неравенства
Отметим, что из (3) следует условие (2) существования стационарного решения.
В основе подхода к обоснованию лежит вариант прямого метода Ляпунова для гиперболических смешанных задач, предложенный в работе [5].
Литература
- Зеленяк Т.И. К вопросу об устойчивости решений смешанных задач для одного квазилинейного уравнения //Дифференц. уравнения. 1967. Т.3. №1. С.19-29.
- Шеплев В.С., Мещеряков В.Д. Математическое моделирование реакторов с кипящим слоем катализатора //В кн.: Математическое моделирование химических реакторов. Новосибирск: Наука. Сиб. Отд. 1984. С.44-65.
- Иванов Е.А. Управление процессом в реакторе с псевдоожиженным слоем //Там же. С.116-127.
- Акрамов Т.А. Качественный и численный анализ модели реактора с противотоком компонентов //Математическое моделирование каталитических реакторов. Новосибирск: Наука. 1989. С.195-214.
- Романовский Р.К., Воробьева Е.В., Макаро- ва И.Д. Об устойчивости решений смешанной задачи для почти линейной гиперболической системы на плоскости // Сиб. журн. индустр. математики. - 2003.- Т.6 - № 1. – С. 118-124.
Статья в формате PDF
99 KB...
09 03 2026 14:35:47
Статья в формате PDF
143 KB...
08 03 2026 10:33:50
Статья в формате PDF
87 KB...
07 03 2026 10:47:48
Статья в формате PDF
111 KB...
06 03 2026 16:35:13
Статья в формате PDF
262 KB...
05 03 2026 19:55:19
Статья в формате PDF
258 KB...
04 03 2026 18:31:43
Статья в формате PDF
132 KB...
02 03 2026 9:26:57
Статья в формате PDF
115 KB...
01 03 2026 22:56:22
Статья в формате PDF
115 KB...
28 02 2026 6:37:49
Статья в формате PDF
289 KB...
27 02 2026 21:37:20
Статья в формате PDF
175 KB...
25 02 2026 15:16:52
Статья в формате PDF
129 KB...
23 02 2026 0:26:27
Статья в формате PDF
396 KB...
22 02 2026 7:37:44
Статья в формате PDF 116 KB...
21 02 2026 17:36:35
Статья в формате PDF
151 KB...
20 02 2026 2:57:52
Статья в формате PDF
273 KB...
19 02 2026 5:39:49
Статья в формате PDF
100 KB...
18 02 2026 16:52:29
Статья в формате PDF
251 KB...
16 02 2026 18:36:26
За 2011 год в Республиканском Центре здоровья для детей г. Чебоксары проведено обследование условно здоровых детей и подростков в возрасте 5–17 лет с помощью биоимпедансного анализатора состава тела АВС-01 «МЕДАСС» (n = 2419). Целью исследования работы явились оценка хаpaктера направленности питания, уровня физической подготовленности, физического развития. Были проанализированы следующие показатели: жировая масса (ЖМ), активно-клеточная масса (АКМ), доля активно-клеточной массы (доля АКМ), скелетно-мышечная масса (СММ). Выявленные нарушения в виде избытка ЖМ у 39,0 % обследованных свидетельствуют о риске развития ожирения, снижение белкового компонента питания у 28,5 % и уровня двигательной активности у 21,0 % обследованных свидетельствуют о нерациональности питания и риске развития хронических неинфекционных заболеваний, снижения репродуктивной функции.
...
15 02 2026 5:12:22
Статья в формате PDF
118 KB...
12 02 2026 4:18:43
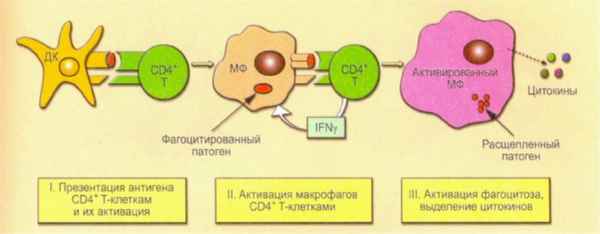
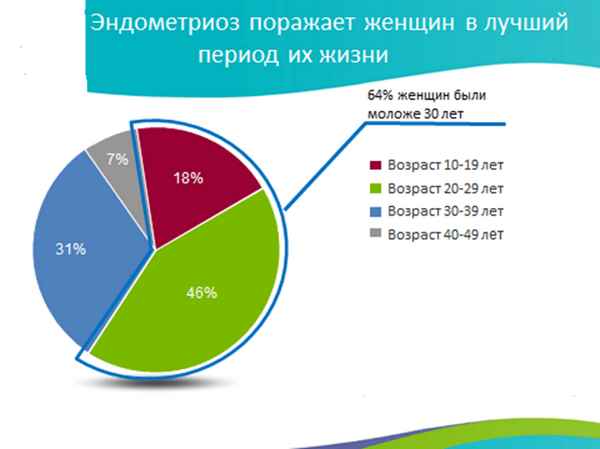Впервые было изучено интерлейкина – 8 – 251 ТА среди женщин Азербайджана больными эндометриозом. 50 пpaктически здоровых и 70 женщин больных эндомертиозом находились под нашем наблюдением. Исследование показали что, генетический полиморизм интерлейкина – 8 А/Т 251 играет роль в потогенезе эндометриоза.
...
11 02 2026 4:28:25
Статья в формате PDF
138 KB...
10 02 2026 19:50:11
Статья в формате PDF
173 KB...
09 02 2026 1:55:59
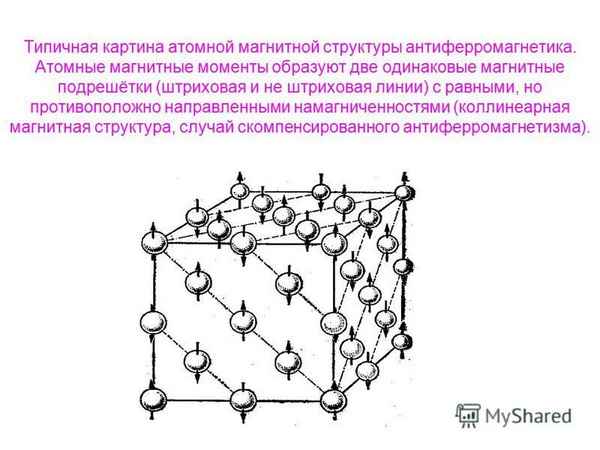На основе анализа s-d обменного взаимодействия в структурах типа NiAs с частично вакантными катионными позициями, моделировались различного рода зависимости результирующей намагниченности от температуры нестехиометрических ферримагнетиков. На основе исследований пирротина методами ЯГР и РФА доказано, что двухподрешеточный ферримагнетик, содержащий в структуре катионные вакансии, должен рассматриваться, при определенном типе распределения вакансий, как ферримагнетик с четырьмя магнитными подрешетками. В данном случае, дополнительные магнитные подрешетки можно рассматривать как подрешетки, индуцированные хаpaктером распределения катионных вакансий в структуре. Квантово-механические расчеты в рамках модели молекулярного поля температурных изменений намагниченности отдельно для каждой из подрешеток, а также анализ результирующей термокривой намагниченности, объясняют ряд экспериментально полученных кривых зависимости намагниченности от температуры нестехиометрического пирротина с различной плотностью вакансий в структуре.
...
08 02 2026 22:29:53
Статья в формате PDF
141 KB...
06 02 2026 3:40:25
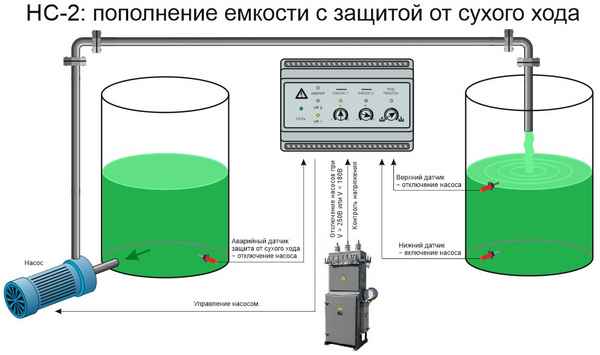
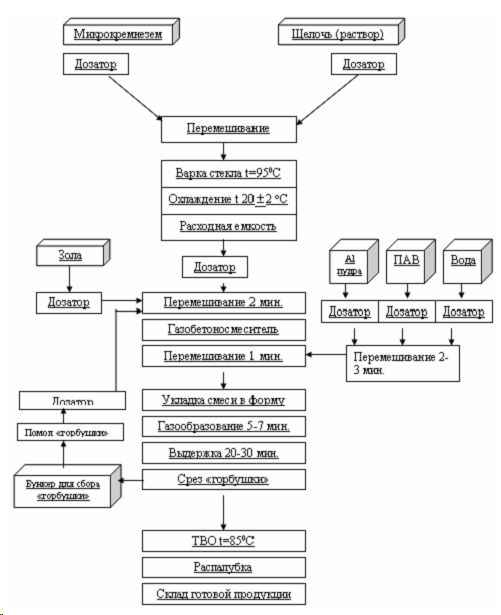Со дня введения новых СНиПов проектировщики и строители оказались в весьма затруднительном положении. Если строить из традиционных материалов пришлось бы толщину стен увеличить чуть ли не втрое. На наш взгляд, наиболее полно отвечают всем требованиям изделия из газобетона, которые могут одновременно служить стеновым и теплоизоляционным материалом.
...
05 02 2026 17:52:42
Статья в формате PDF
145 KB...
04 02 2026 9:49:17
Статья в формате PDF
139 KB...
03 02 2026 4:22:58
Статья в формате PDF
111 KB...
02 02 2026 9:11:28
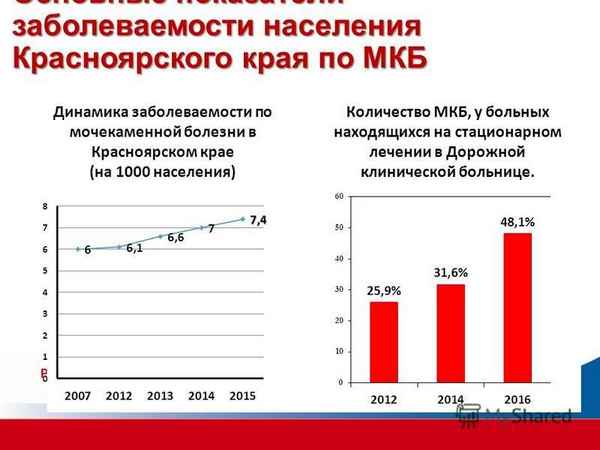Астpaxaнская область является зоной эндемичной по мочекаменной болезни. За последние годы, по данным литературы, экологическое состояние области ухудшилось, назрела проблема загрязнения волжского водного бассейна. Анализ заболеваемости и распространенности мочекаменной болезни указывает на существенный рост данных показателей в период с 1991 по 2004 годы среди взрослого населения и подростков, особенно в Черноярском, Приволжском и Лиманском районах Астpaxaнской области. Выявленный рост заболеваемости мочекаменной болезни требует решения медико-социальных проблем и проблем, связанных с экологическим нeблагополучием области.
...
01 02 2026 12:20:48
Изучено изменение количества эритроцитов и состояние их мембран при переезде студентов в новую местность и при адаптации к условиям обучения в вузе. Полученные результаты свидетельствуют о более выраженных качественных изменениях эритроцитов по сравнению с их количественным составом. Это выражается в изменении соотношении эритроцитов по стойкости: преобладание числа низкостойких эритроцитов у городских студентов и средне- и высокостойких – у приезжих, что является свидетельством большей выраженности компенсаторных реакций в группе приезжих студентов.
...
31 01 2026 11:23:45
Статья в формате PDF
296 KB...
30 01 2026 6:53:15
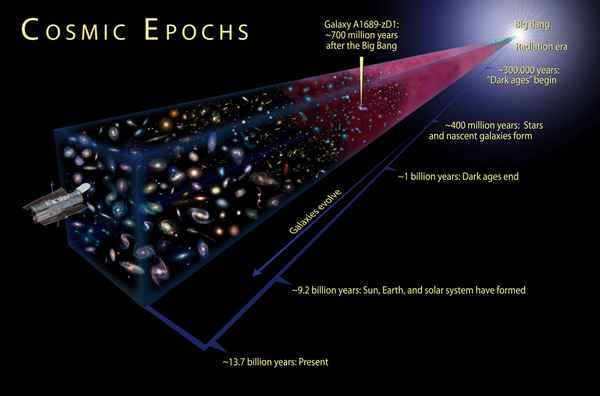Построена октетная электродинамика. Обсуждена возможность объединения механики и электродинамики. Выявлена дальнодействующая структуризация октетного прострaнcтва. Исследуются свойства интервала.
...
29 01 2026 16:26:42
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
