МАЛЫЕ КОЛЕБАНИЯ ПРИЗМАТИЧЕСКОГО БРУСКА НА ЦИЛИНДРЕ
На цилиндрическую поверхность радиуса положен призматический брусок с прямоугольным поперечным сечением высоты 2b. Радиус инерции бруска вокруг оси, проходящей через его центр масс и параллельный оси бруска равен ic.
Взяв за параметр, определяющий положение бруска угол q его наклона к горизонту, выражаем через него кинетическую энергию T и потенциальную энергию П. По теореме Кёнига [1]:
(1)
Здесь M - масса бруска, а - его момент инерции относительно оси, проходящей через центр масс сечения.
Призматический брусок на цилиндрической поверхности
Чтобы вычислить скорость центра масс бруска Vc, возьмём начало координат в точке O касания бруска и цилиндра при равновесии. Так как при колебаниях брус катится без скольжения, то CB = OA = Rq. Для нахождения координаты центра масс (точки C), проектируем на координатные оси векторную сумму
тогда
(2)
Дифференцируя формулы (2), найдём проекции вектора скорости на оси координат [2]:
Таким образом, формула кинетической энергии (1) принимает вид:
Считая колебания малыми, можно предположить, что θ2 ≈ 0, тогда:
(3)
Потенциальная энергия
(4)
Определим постоянную C при условии, что П = 0, если θ = 0,
или .
Введём константу C в формулу (4) и получим:
Полагая sinθ ≈ j, cosθ ≈ 0, получим:
(5)
Вводя формулы (3) и (5) в уравнение Лагранжа, получим:
или
(6)
Уравнение (6) представляет собой дифференциальное уравнение малых колебаний, циклическая частота которых и период колебаний τ определяются формулами:
Т.о. для малых колебаний призматического бруска на круговом цилиндре при отсутствии проскальзывания получено разрешающее уравнение колебательного процесса, определена циклическая частота и период колебаний.
Статья в формате PDF
99 KB...
23 04 2024 7:27:51
Статья в формате PDF
251 KB...
22 04 2024 22:33:54
Статья в формате PDF
105 KB...
21 04 2024 20:12:12
Статья в формате PDF
102 KB...
20 04 2024 9:40:19
Статья в формате PDF
244 KB...
19 04 2024 8:14:22
Статья в формате PDF
357 KB...
18 04 2024 11:26:49
Статья в формате PDF
127 KB...
17 04 2024 0:14:50
Статья в формате PDF
103 KB...
16 04 2024 19:40:30
Статья в формате PDF
305 KB...
15 04 2024 13:28:26
Статья в формате PDF
113 KB...
13 04 2024 6:53:29
Статья в формате PDF
269 KB...
11 04 2024 0:39:32
Статья в формате PDF
274 KB...
10 04 2024 23:39:48
Статья в формате PDF
124 KB...
09 04 2024 11:35:55
Статья в формате PDF
120 KB...
08 04 2024 13:25:10
Статья в формате PDF
270 KB...
05 04 2024 6:56:26
Статья в формате PDF
101 KB...
04 04 2024 15:10:16
Статья в формате PDF
115 KB...
03 04 2024 22:29:28
Статья в формате PDF
420 KB...
02 04 2024 6:52:14
Статья в формате PDF
266 KB...
01 04 2024 23:13:36
Статья в формате PDF
114 KB...
31 03 2024 0:36:22
Статья в формате PDF
108 KB...
30 03 2024 4:31:28
Статья в формате PDF
122 KB...
29 03 2024 22:25:39
Статья в формате PDF
140 KB...
28 03 2024 17:21:54
Статья в формате PDF
274 KB...
27 03 2024 11:44:58
Статья в формате PDF
120 KB...
26 03 2024 18:48:32
Статья в формате PDF
123 KB...
25 03 2024 22:28:35
Статья в формате PDF
140 KB...
24 03 2024 10:17:43
Статья в формате PDF
306 KB...
23 03 2024 6:53:32
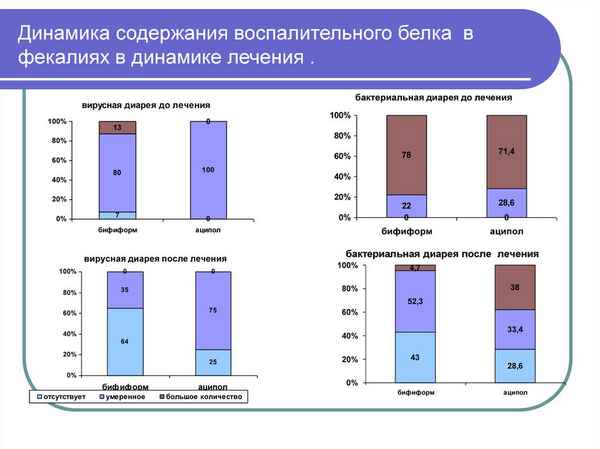Изучено влияние солей кадмия, свинца и марганца на содержание белков в сыворотке крови сеголеток карпа. Показаны разнонаправленные изменения белкового состава сыворотки крови рыб при воздействии солей тяжелых металлов, о чем можно судить на основании изменения А/G индекса. При хроническом действии ионов кадмия отмечено значительное преобладание суммарного содержания альбуминов над глобулинами на протяжении всего эксперимента, пребывание рыб в среде с ионами свинца сопровождалось более значительным ростом содержания глобулинов, тогда как при действии ионов марганца не выявлен однонаправленный хаpaктер изменения соотношения альбуминов и глобулинов.
...
22 03 2024 10:11:10
Статья в формате PDF
251 KB...
21 03 2024 21:23:21
Статья в формате PDF
113 KB...
20 03 2024 11:30:39
Статья в формате PDF
266 KB...
18 03 2024 3:24:18
Статья в формате PDF
94 KB...
17 03 2024 23:21:37
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
