РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРОГНОЗИРОВАНИЯ ЗАБОЛЕВАЕМОСТИ КЛЕЩЕВЫМ ЭНЦЕФАЛИТОМ
Математическое моделирование эпидемических процессов (ЭП) позволяет осуществлять качественный долгосрочный прогноз инфекционной заболеваемости, выявлять факторы, влияющие на динамику ЭП. В 70-х годах ХХ столетия Л.Н. Большев с соавторами [2, 3] разработали математическую модель прогноза заболеваемости клещевым энцефалитом (КЭ). Для построения модели авторы провели предварительный анализ влияния частоты присасывания клещей и иммунной прослойки населения всех возрастов на частоту заболеваний КЭ. Е.И.Болотин с соавторами [1] разработали методику факторного временного прогнозирования эпидемических проявлений очагов КЭ с использованием выявленных критических уровней заболеваемости.
Нами для разработки математического моделирования ЭП использована многолетняя динамика заболеваемости КЭ на юге Тюменской области и составлены временные ряды в климатических подзонах. Математическая модель позволила без предварительного анализа факторов, влияющих на ЭП, осуществлять прогноз заболеваемости КЭ.
По анализу временных рядов можно предсказать будущие значения временного ряда на основании предыдущих фактических данных [5]. В процессе составления временного ряда необходимо идентифицировать и формально описать его. Как только математическая модель будет определена, ее можно экстраполировать, не обращая внимания на процессы, влияющие на изменение показателей временного ряда.
Данный метод использован нами для изучения динамики ЭП, вызванного вирусом КЭ. Сложность возникла при идентификации временного ряда. При монотонном тренде происходит устойчивое нарастание или убывание значений временного ряда. Анализировать такой ряд обычно нетрудно. В качестве экстраполирующей функции ряда чаще всего выбирают известные математические зависимости - линейные, параболические, экспоненциальные и др., которые часто не отражают динамику ЭП. Прогнозируемые значения такого ряда будут являться оценочными и не обеспечивают точности расчётов.
Реже используют полиномиальное преобразование временного ряда. Сглаживание ряда с помощью полиномов связано с проведением трудоёмких вычислений, что не позволяет широко использовать данный метод для прогноза инфекционной заболеваемости, и в научной литературе сведения о применении полиномиального метода для этих целей отсутствуют.
Для прогнозирования заболеваемости КЭ нами использована аддитивная модель и временной ряд был представлен функциональной зависимостью:
y(t) = f(t) + s(t) + ε(t), (1)
где y(t) - значение временного ряда в момент времени t; f(t) - основная составляющая ряда (тренд); s(t) - сезонная составляющая (отражает повторяемость показателей заболеваемости в течение сезона года); ε(t) - случайная компонента (отражает неучтённые и случайные факторы, влияющие на ЭП). Временные ряды могут содержать одновременно все перечисленные компоненты или их различные комбинации. Такой ряд называют временным с сезонной составляющей.
Для получения тренда использовано уравнение полинома Чебышева высокого порядка, что позволило снизить погрешности в прогнозе заболевания. Аппроксимирующая функция f(t) теоретически может быть выражена многочлeном любой степени m, например:
(2)
При каждом повышении порядка полинома требуется определение не только нового параметра, αm+1, но ввиду изменения системы "нормальных уравнений", проводят пересчет всех остальных параметров: от αo до αm.
Рассмотрев общий случай использования метода наименьших квадратов, П. Л. Чебышев разработал метод вычисления уравнения регрессии, позволяющий определять добавляемый параметр без пересчета найденных ранее параметров, ограничиваясь лишь вычислением нового параметра. Добавляемый члeн имеет вид: , где определяется по общей формуле:
(3)
В этом случае уравнение регрессии принимает вид [4]:
(4)
После нахождения уравнения тренда вычисляют остаточную дисперсию по формуле:
, (5)
где n-m-1 - степень свободы, m - степень полинома, n - объём выборки.
Для получения Sm применяют формулу:
, (6)
где - значение ординаты, рассчитанное по уравнению полинома m - степени. Переход к многочлeнам более высокого порядка производят до тех пор, пока остаточная дисперсия продолжает уменьшаться. Если остаточная дисперсия при выравнивании по многочлeну m+1 порядка по сравнению с остаточной дисперсией, полученной для уравнения порядка m, уменьшается незначительно, переход к уравнениям более высокого порядка следует прекратить и аппроксимацию считать достаточной.
Ошибка расчёта (среднеквадратическое отклонение полученной функции от экспериментальных точек) должно быть одного порядка с погрешностью введённых табличных данных, так как среднеквадратическое отклонение зависит от у, n и вида выбранной функции y*. Вычисляют среднеквадратическое отклонение полученной теоретической кривой y* от экспериментальной у:
(7)
и сравнивают с погрешностью эксперимента ε. При этом возможно:
1) δn> ε- аппроксимация слишком грубая, степень полинома необходимо увеличить;
2) δn < ε - аппроксимация физически недостоверна, истинная функция "сплющена", старшие степени полинома лишние и, следовательно, надо уменьшить степень полинома;
3) δn ≈ ε- степень полинома оптимальна.
Погрешность эксперимента рассчитывали по формуле:
, (8)
где yi - наблюдаемые значения, - среднее значение введённых параметров, n - объём выборки.
Аппроксимирующая функция для строго периодической сезонной составляющей s(t) в уравнении (1) находили, используя тригонометрическую функцию, приподнятую над осью t и сдвинутую вдоль неё, в виде:
s(t) = ao + a1 + b1 (9)
В нашем случае, будучи периодической и заданной в виде таблицы, сезонная составляющая не являлась синусоидой, но была близка к ней. Изменив масштаб по оси t в раз ( - число полупериодов сезонной составляющей) получили:
s(t) = ao + a1 cos(z) + b1sin(z) (10)
Сжатие графика по оси t не изменит табличные значения s(t) и коэффициентов ao, a1, b1. Коэффициенты ao, a1, b1 определялись из уравнения (10) методом наименьших квадратов. Была получена система из трёх уравнений, после решения которой, получены формулы для расчёта коэффициентов:
b1=
a1=
ao=
zi= (11)
Функция s(t) определена на отрезке [1, N] не симметрично точке t=0. Поэтому, после вычисления коэффициентов по уравнениям (11), следует сдвинуть функцию s(t), заменив аргумент в формуле (9) на выражение:
(12)
Аппроксимация тригонометрическим многочлeном менее точная, чем например степенная иди другая, но к ней прибегают если функция строго периодическая. Для более точного расчёта ao, a1, b1 необходимо точно определить период сезонной составляющей вводимого временного ряда.
Условие δn ≈ ε - степень полинома оптимальна, выполнялось для уравнения тренда с учётом сезонной составляющей.
Весь алгоритм расчётов по формулам 2 - 12 можно автоматизировать. Нами была составлена компьютерная программа, которая позволяет провести полиномиальную аппроксимацию высокого порядка (8 порядка и выше) значений функций заданных таблично. Используя полученное уравнение тренда, проводили прогнозирование заболеваемости. Программы составлены для ПК, работающие в среде Microsoft Windows на программном языке Visual Basik.
Для составления данной программы использована база данных «Tumklech» [8]. Фактическая заболеваемость КЭ была переведена в показатели заболеваемости на 100 тыс. населения. Анализ тренда проводили в два этапа: определяли наличие тренда и выделяли тренд. Для определения наличия тренда использован критерий Стьюдента, позволяющий выявить различие выборочных средних двух половинок временного ряда. Если различие значимо, то гипотеза о наличии тренда не отвергалась. Для выделения тренда использовали модель простого статистического ряда и аддитивную модель временного ряда (временной ряд с сезонной составляющей).
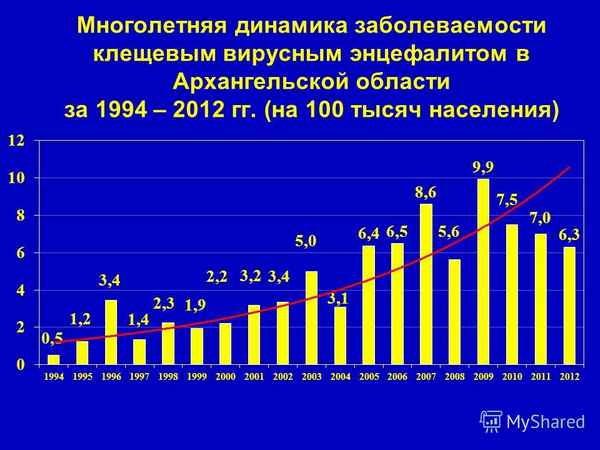
В динамике заболеваемости КЭ хаpaктерна трехлетняя цикличность и в течение сезона года (с 1.04 по 30.09) также наблюдались колебания в показателях заболеваемости. Усреднив значения ряда в соответствии с трёхлетней цикличностью, получим сезонные колебания заболеваемости для каждого года трехлетнего цикла [7]. Однако для долгосрочного прогноза, предложенный способ прогноза будет недостаточно точным.
Известно, что в природе существуют циклические колебания погоды, связанные с цикличностью излучения Солнца. Большой цикл Солнца длится 11 лет. Он связан с цикличностью образования солнечных пятен. 1979-1982 годы максимальной активности; 1986-1987 годы минимальной активности. В настоящее время Солнечная активность минимальная [6].
Методом дисперсионного анализа нами также установлено наличие многолетнего цикла в динамике заболеваемости КЭ. В 1999г. наблюдалась максимальная заболеваемость КЭ во всех климатических подзонах юга Тюменской области.
Применение многолетней цикличности к нашим расчётам, означает усложнение модели временного ряда ещё одной составляющей, зависящей от многолетней цикличности. В этом случае прогноз модели будет точнее. Условно назовём эту модель - аддитивная модель с двумя составляющими. Уравнение этой модели:
y(t) =f(t) + e1(t) + e2(t), (13)
где ε1(t) - сезонная составляющая с трёхлетним периодом, ε2(t) -сезонная составляющая с многолетним периодом. Данная модель может быть использована для долгосрочного прогнозирования заболеваемости КЭ.
СПИСОК ЛИТЕРАТУРЫ:
- Болотин Е.И., Цициашвили Г.Ш., Голычева И.В. // Паразитология. - 2002. - Т.36.- Вып. 2. - С.89.
- Большев Л.Н., Гольдфарб Л.Г. // Вопросы эпидемиологии и профилактики клещевого энцефалита. - М., 1970. - С. 154.
- Большев Л.Н., Гольдфарб Л.Г., Круопис Ю.И. // Вопросы эпидемиологии и профилактики клещевого энцефалита. - М., 1970. - С. 171.
- Венецкий И.Г., Кильдишев Г.С. Теория вероятности и математическая статистика. - М., «Статистика». - 1975. - 264 с.
- Ивашев-Мусатов О.С. Теория вероятности и математическая статистика. - М., «Наука». - 1979. - 254 с.
- Ишков В.Н. «Вселенная и мы» http://www.астронет.ru/ / Солнце в текущем 23 цикле солнечной активности.
- Козлов Л.Б., Кашуба Э.А., Цокова Т.Н. и др. Способ прогноза заболеваемости клещевыми инфекциями // Патент RU 2294697 С2. - Бюл. № 7 от 10.03.2007г.
- Козлов Л.Б., Цокова Т.Н., Огурцов А.А. и др. / Заболеваемость клещевым энцефалитом в Тюменской области «Tumklech» // База данных. - Свидетельство №2007620363 от 18.10.2007. - Правообладатель: ФГУЗ «Центр гигиены и эпидемиологии в Тюменской области».
23 04 2024 8:21:57
22 04 2024 1:57:47
20 04 2024 10:28:25
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
19 04 2024 16:35:30
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
18 04 2024 22:43:41
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
17 04 2024 11:53:46
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
16 04 2024 8:57:53
 Статья в формате PDF
235 KB...
Статья в формате PDF
235 KB...
14 04 2024 13:51:34
Статья в формате PDF 283 KB...
13 04 2024 5:39:59
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
12 04 2024 16:10:38
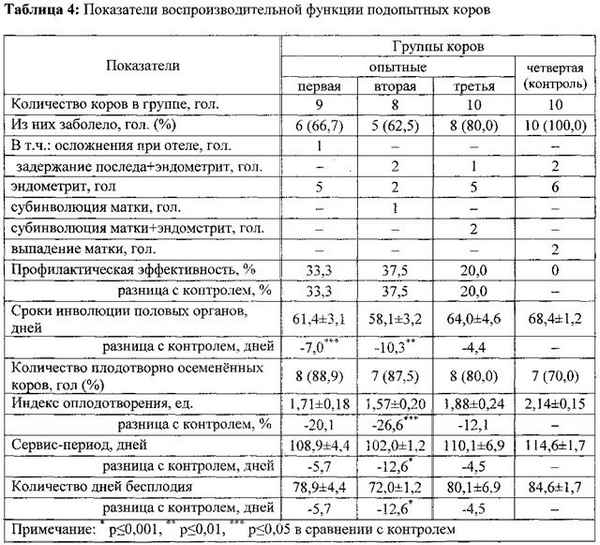 В данной работе представлены материалы по изучению влияния добавок серы к рациону крупного рогатого скота с целью коррекции иммуннобиохимического статуса при хроническом селеновом токсикозе.
...
В данной работе представлены материалы по изучению влияния добавок серы к рациону крупного рогатого скота с целью коррекции иммуннобиохимического статуса при хроническом селеновом токсикозе.
...
11 04 2024 12:30:45
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
10 04 2024 9:10:15
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
09 04 2024 12:33:23
08 04 2024 20:58:56
 Статья в формате PDF
249 KB...
Статья в формате PDF
249 KB...
07 04 2024 2:32:15
 Статья в формате PDF
264 KB...
Статья в формате PDF
264 KB...
02 04 2024 5:16:52
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
01 04 2024 14:32:37
 В статье дается концептуальное видение профессиональных стилей человека в зависимости от его профессиональных и жизненных приоритетов. Стиль отражает стратегию адаптации человека. Индивидуальный стиль профессиональной деятельности рассматривается как функция составляющих ее эффективности. Выделено 16 вариантов стилей, в зависимости от значимых для человека составляющих эффективности его труда. В зависимости от профессиональной успешности, степени удовлетворенности трудом и ценностных ориентаций выделено 8 профессиональных стилей, хаpaктеризующих (выявляющих, демонстрирующих) хаpaктер специалиста.
...
В статье дается концептуальное видение профессиональных стилей человека в зависимости от его профессиональных и жизненных приоритетов. Стиль отражает стратегию адаптации человека. Индивидуальный стиль профессиональной деятельности рассматривается как функция составляющих ее эффективности. Выделено 16 вариантов стилей, в зависимости от значимых для человека составляющих эффективности его труда. В зависимости от профессиональной успешности, степени удовлетворенности трудом и ценностных ориентаций выделено 8 профессиональных стилей, хаpaктеризующих (выявляющих, демонстрирующих) хаpaктер специалиста.
...
31 03 2024 13:18:47
 В статье дано математическое описание процесса образования градиентных оксидных покрытий в микроплазменном режиме для случая, когда лимитирующей стадией процесса является стадия доставки ионов из раствора электролита к поверхности электрода.
Статья может быть полезна исследователям и пpaктикам, изучающим и использующим микроплазменные процессы для получения оксидных и керамических покрытий в растворах электролитов.
...
В статье дано математическое описание процесса образования градиентных оксидных покрытий в микроплазменном режиме для случая, когда лимитирующей стадией процесса является стадия доставки ионов из раствора электролита к поверхности электрода.
Статья может быть полезна исследователям и пpaктикам, изучающим и использующим микроплазменные процессы для получения оксидных и керамических покрытий в растворах электролитов.
...
30 03 2024 18:11:18
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
29 03 2024 23:40:58
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
28 03 2024 14:16:38
 В статье отражены результаты комплексного исследования подготовленности спортсменок, специализирующихся в беге на 300-400 м с барьерами. Дан анализ статистически достоверных различий по педагогическим, физиологическим и биометрическим показателям в ответственейший момент спортивной карьеры - момент перехода с «детской» дистанции (бега на 300 м с барьерами) на олимпийскую дисциплину (400 м с барьерами). Выявлены взаимосвязи между различными сторонами подготовленности: физической, функциональной и технической. Представленный материал можно использовать в виде модельных хаpaктеристик для дeвyшек в возрасте 15-16 лет и закономерностей становления спортивного мастерства при уточнении Учебной программы для детско-юношеских спортивных школ, специализированных детско-юношеских школ олимпийского резерва и школ высшего спортивного мастерства по разделу «Барьерный бег».
...
В статье отражены результаты комплексного исследования подготовленности спортсменок, специализирующихся в беге на 300-400 м с барьерами. Дан анализ статистически достоверных различий по педагогическим, физиологическим и биометрическим показателям в ответственейший момент спортивной карьеры - момент перехода с «детской» дистанции (бега на 300 м с барьерами) на олимпийскую дисциплину (400 м с барьерами). Выявлены взаимосвязи между различными сторонами подготовленности: физической, функциональной и технической. Представленный материал можно использовать в виде модельных хаpaктеристик для дeвyшек в возрасте 15-16 лет и закономерностей становления спортивного мастерства при уточнении Учебной программы для детско-юношеских спортивных школ, специализированных детско-юношеских школ олимпийского резерва и школ высшего спортивного мастерства по разделу «Барьерный бег».
...
27 03 2024 3:36:12
 Статья в формате PDF
244 KB...
Статья в формате PDF
244 KB...
26 03 2024 17:12:16
 Статья в формате PDF
136 KB...
Статья в формате PDF
136 KB...
25 03 2024 5:59:25
 Статья в формате PDF
275 KB...
Статья в формате PDF
275 KB...
23 03 2024 21:58:37
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
22 03 2024 5:20:15
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
21 03 2024 18:47:58
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
20 03 2024 7:42:19
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
18 03 2024 5:37:25
 В работе исследовалось изменение метаболизма коллагена при остром стрессе у крыс с различным эмоциональным статусом. Острый стресс индуцировали, помещая животных в пластиковые камеры с отверстием для доступа воздуха на 1 час, 2,5 часа и 6 часов. Наблюдалось различие в реакции гипоталамо-гипофизарно-надпочечниковой системы и динамике показателей метаболизма коллагена у крыс с разным эмоциональным статусом.
...
В работе исследовалось изменение метаболизма коллагена при остром стрессе у крыс с различным эмоциональным статусом. Острый стресс индуцировали, помещая животных в пластиковые камеры с отверстием для доступа воздуха на 1 час, 2,5 часа и 6 часов. Наблюдалось различие в реакции гипоталамо-гипофизарно-надпочечниковой системы и динамике показателей метаболизма коллагена у крыс с разным эмоциональным статусом.
...
16 03 2024 14:58:25
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::