КОМПЬЮТЕРНАЯ ОПТИМИЗАЦИЯ НЕПРЕРЫВНЫХ ФУНКЦИЙ С МНОГОМЕРНЫМ АРГУМЕНТОМ НА ЗАДАННОМ МНОЖЕСТВЕ С ПРИМЕНЕНИЕМ МЕТОДОВ ОПТИМИЗАЦИИ И ЭВРИСТИЧЕСКИХ АЛГОРИТМОВ
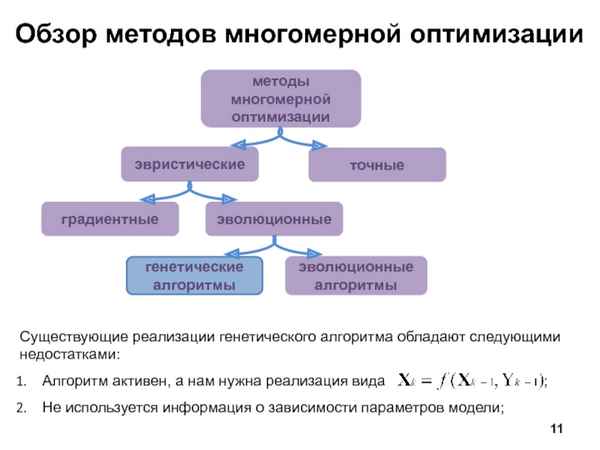
На данный момент в науке существует множество методов поиска экстремума функции многих переменных. Все они различаются предъявляемыми к функции требованиями и обеспечивают разную эффективность и быстродействие. Очевидно, что хороший результат может быть достигнут путём объединения нескольких методов.
Рассмотрим алгоритм программы, сочетающей метод штрафных функций, генетический алгоритм и метод покоординатного спуска. Такая программа позволяет быстро находить экстремум функции многих переменных на множестве, задаваемом ограничениями в виде равенств и неравенств. С точки зрения структуры, её можно разделить на четыре блока, которые и будут рассмотрены ниже.
На первом этапе пользователем программы задаются все исходные данные: рассматриваемая функция и ограничения, определяющие множество значений аргументов. Затем применяется метод штрафных функций [1], в процессе которого исходная функция преобразуется к новому виду, включающему в себя ограничения. Все последующие операции выполняются уже только с этой новой функцией.
Следующий блок программы осуществляет преобразование функции в обратную польскую запись. Затем эта запись обpaбатывается с целью вычлeнения переменных и занесения их в память.
Третий блок является ключевым блоком программы: в нём происходит основной вычислительный процесс на основе применения генетического алгоритма [2]. Сначала формируются случайные наборы значений аргументов, представляющие собой точки начального приближения. Затем начинается итерационный процесс. Первой частью его является вычисление значений функции на текущих наборах, фиксирование нового значения экстремума, если таковое появляется, и вычисление коэффициентов «выживаемости» наборов, то есть близости значений функции на них к экстремуму. Эти коэффициенты нормированы так, что их сумма по всем наборам даёт 100%. Второй частью итерационного процесса является процеДypa выбора родителей для наборов следующего поколения. Этот выбор осуществляется случайным образом с учётом коэффициентов «выживаемости» наборов: чем больше коэффициент, тем больше шанс набора стать родителем. В третьей части происходит кроссовер, то есть для каждого нового набора выбирается точка разрыва, все значения переменных до которой заимствуются у одного родителя, а после которой - у второго. В последней части для каждого нового набора выбирается мутирующая переменная, значение которой изменяется случайным образом. После этого новые наборы становятся текущими, и на этом итерационный процесс заканчивается. Итерации повторяются до тех пор, пока разность между модулями последних найденных значений экстремума не станет меньше 0.001 модуля значения экстремума.
Четвёртый блок программы призван за небольшое число итераций уточнить полученный результат. Это осуществляется посредством использования метода покоординатного спуска. Точкой начального приближения для него выступает набор значений аргументов, полученный в результате применения генетического алгоритма.
Таким образом, подобное сочетание нескольких методов позволяет преодолеть недостатки каждого из них и получить достаточно точное решение задачи поиска глобального экстремума функции многих переменных на множестве, задаваемом ограничениями, за достаточно небольшое количество итераций.
По поводу актуальности этого алгоритма можно сказать следующее. Актуальность поиска экстремума функции очевидна, так как многие прикладные задачи требуют нахождения оптимального решения, которым, как правило, и оказывается наименьшее или наибольшее значение функции, определяемой задачей. Актуальность же использования именно этого алгоритма для поиска экстремума функции следует из эффективного взаимодействия всех блоков программы и основывается на следующих преимуществах: глобальность находимого решения, высокая точность, высокое быстродействие, возможность оперирования с множествами, задаваемыми ограничениями.
Данная система успешно себя показала при планировании расходов бюджета в части целевых программ Владимирской области. С помощью логистической функции экспертным путем была оценена эффективность этих программ в зависимости от их финансирования. С помощью вышерассмотренной системы стало возможным получение в течение нескольких минут высокоэффективное распределение финансирования программ.
СПИСОК ЛИТЕРАТУРЫ:
- Васильев Ф.П. Численные методы решения экстремальных задач. - М. : Наука, 1988. - 556 с.
- Генетические алгоритмы [Электронный ресурс]. Проект AlgoList - алгоритмы, методы, исходники, 2008. Режим доступа: http://algolist.ru/ ai/ga/index.php
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
24 04 2024 10:59:13
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
22 04 2024 8:26:23
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
21 04 2024 11:28:31
 В статье дано определение техническому состоянию техники, представлены виды технических состояний и процессы изменения технического состояния при эксплуатации. Бытовая техника при эксплуатации может принимать исправное и неисправное состояние, а также работоспособное и неработоспособное состояние. Показана взаимосвязь видов технических состояний в виде графа переходов технических состояний, позволяющий проводить технологию восстановления работоспособности техники. Определен порядок восстановления бытовой техники и сформулирован критерий отказа техники. Рассмотрены признаки восстановления бытовой техники по отношению к восстанавливаемой и невосстанавливаемой техники. Показано, что к невосстанавливаемой технике относится техника, нахоящаяся в предельном состоянии или в результате ресурсного отказа. Рассмотрены признаки предельного состояния для восстанавливаемой и невосстанавливаемой техники.
...
В статье дано определение техническому состоянию техники, представлены виды технических состояний и процессы изменения технического состояния при эксплуатации. Бытовая техника при эксплуатации может принимать исправное и неисправное состояние, а также работоспособное и неработоспособное состояние. Показана взаимосвязь видов технических состояний в виде графа переходов технических состояний, позволяющий проводить технологию восстановления работоспособности техники. Определен порядок восстановления бытовой техники и сформулирован критерий отказа техники. Рассмотрены признаки восстановления бытовой техники по отношению к восстанавливаемой и невосстанавливаемой техники. Показано, что к невосстанавливаемой технике относится техника, нахоящаяся в предельном состоянии или в результате ресурсного отказа. Рассмотрены признаки предельного состояния для восстанавливаемой и невосстанавливаемой техники.
...
20 04 2024 4:48:33
 В данной статье осуществлены анализ и обощение зарубежных психологических концепций, объясняющих активность человека в отношении своего здоровья, и на этой основе дано авторское определение понятия «здоровьесозидающий потенциал личности». Особое внимание авторы уделяют рассмотрению структуры здоровьесозидающего потенциала, описанию психологических механизмов его формирования и выявлению закономерностей его развития в различные возрастные периоды. Авторами впервые представлена и научно обоснована векторная модель здоровьесозидающего потенциала личности, показаны её возможности при выявлении психологических детерминант, влияющих на показатели целостного здоровья человека.
...
В данной статье осуществлены анализ и обощение зарубежных психологических концепций, объясняющих активность человека в отношении своего здоровья, и на этой основе дано авторское определение понятия «здоровьесозидающий потенциал личности». Особое внимание авторы уделяют рассмотрению структуры здоровьесозидающего потенциала, описанию психологических механизмов его формирования и выявлению закономерностей его развития в различные возрастные периоды. Авторами впервые представлена и научно обоснована векторная модель здоровьесозидающего потенциала личности, показаны её возможности при выявлении психологических детерминант, влияющих на показатели целостного здоровья человека.
...
18 04 2024 5:28:55
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
17 04 2024 4:20:16
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
16 04 2024 10:43:26
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
15 04 2024 23:11:26
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
14 04 2024 18:35:48
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
13 04 2024 20:27:57
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
12 04 2024 0:43:45
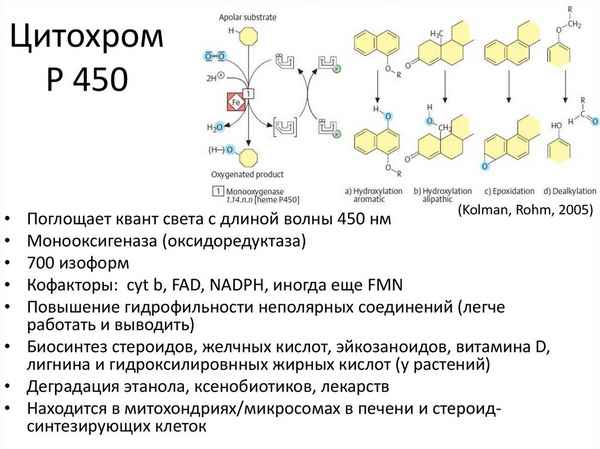 В работе впервые приведены сведения об ассоциации полиморфного ДНК – локуса 256A/G гена переносчика дофамина SLC6A3 и уровней дофамина с повышенной тревожностью крыс с генотипом А2/А2 по локусу TAG 1A DRD2.
...
В работе впервые приведены сведения об ассоциации полиморфного ДНК – локуса 256A/G гена переносчика дофамина SLC6A3 и уровней дофамина с повышенной тревожностью крыс с генотипом А2/А2 по локусу TAG 1A DRD2.
...
11 04 2024 17:58:52
Статья в формате PDF 93 KB...
10 04 2024 5:29:26
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
09 04 2024 19:42:39
 Статья в формате PDF
269 KB...
Статья в формате PDF
269 KB...
08 04 2024 9:51:20
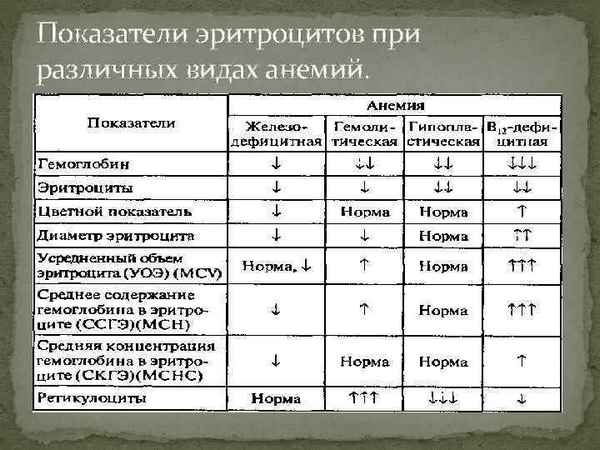
 Возрастные изменения геометрических параметров эритроцитов крови здоровых мужчин проявляются в виде увеличение диаметра, площади поверхности и объема красных клеток крови. У женщин, по сравнению с мужчинами, установлены достоверно более высокие показатели площади поверхности и объема эритроцитов. С возрастом регистрируется повышение жесткости мембран эритроцитов, причем данные изменения более выражены у женщин.
...
Возрастные изменения геометрических параметров эритроцитов крови здоровых мужчин проявляются в виде увеличение диаметра, площади поверхности и объема красных клеток крови. У женщин, по сравнению с мужчинами, установлены достоверно более высокие показатели площади поверхности и объема эритроцитов. С возрастом регистрируется повышение жесткости мембран эритроцитов, причем данные изменения более выражены у женщин.
...
07 04 2024 0:53:26
06 04 2024 9:33:47
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
05 04 2024 1:59:48
 Статья в формате PDF
205 KB...
Статья в формате PDF
205 KB...
04 04 2024 20:26:41
03 04 2024 2:59:56
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
02 04 2024 15:18:20
 Статья в формате PDF
242 KB...
Статья в формате PDF
242 KB...
01 04 2024 4:22:48
31 03 2024 22:38:30
 Статья в формате PDF
266 KB...
Статья в формате PDF
266 KB...
30 03 2024 23:28:34
 Статья в формате PDF
151 KB...
Статья в формате PDF
151 KB...
29 03 2024 7:53:58
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
28 03 2024 4:47:22
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
27 03 2024 10:39:18
24 03 2024 14:42:28
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
22 03 2024 9:10:39
 В статье рассматриваются основные исторические этапы развития отечественной териологии в XVIII-XX вв., самоотверженно проводившиеся учеными-зоологами несмотря на различные трудности, являвшиеся следствием изменения исторической и политической картины мира. Показан вклад отдельных российских ученых в формировании териологии, а также роль в этом процессе научных сообществ России.
...
В статье рассматриваются основные исторические этапы развития отечественной териологии в XVIII-XX вв., самоотверженно проводившиеся учеными-зоологами несмотря на различные трудности, являвшиеся следствием изменения исторической и политической картины мира. Показан вклад отдельных российских ученых в формировании териологии, а также роль в этом процессе научных сообществ России.
...
21 03 2024 13:38:59
 Статья в формате PDF
265 KB...
Статья в формате PDF
265 KB...
20 03 2024 21:29:49
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
19 03 2024 15:47:11
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
18 03 2024 14:29:35
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
17 03 2024 13:19:55
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::