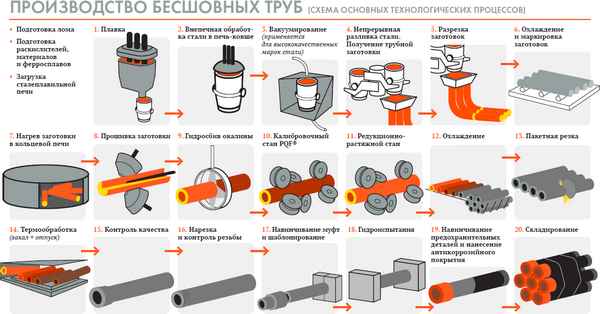
ИСПОЛЬЗОВАНИЕ ГИСТОГРАММНЫХ ОЦЕНОК В ЗАДАЧАХ РАСПОЗНАВАНИЯ
Природа и хаpaктер информативных признаков, используемых при решении задач распознавания, могут быть самыми различными - спектральные плотности эталонных сигналов, автокорреляционные функции, средние значения и т.п. [1]. В том числе достаточно широко используются гистограммные оценки плотностей распределения вероятностей появления значений сигналов, не требующие значительных вычислительных затрат. В зависимости от физической природы сигнала такие оценки могут интерпретироваться по-разному. Например, в системах технического зрения, где в качестве первичного источника информации используются цифровые модели изображений, такие гистограммы хаpaктеризуют распределение вероятностей появления пикселей с заданным уровнем яркости, или, в многомерном случае, с заданным цветовым оттенком.
Оценка плотности распределения по гистограмме будет являться случайной величиной, распределение которой должно зависеть от объёма выборки отсчётов сигнала, по которой формируется эта оценка, а также, возможно, от ряда других факторов. Поэтому для принятия решения о целесообразности её использования как информативного признака, необходимо установить вид этого распределения и его основные параметры.
Пусть - сигнал, воспринимаемый ИИС, подвергшийся дискретизации и квантованию. Здесь η - Nd - мерный обобщённый аргумент, определяющий положение текущего отсчёта в сигнальной области (прострaнcтве, времени, спектральной зоне и т.п.). Каждый отсчёт может принимать одно из конечного множества значений , где n - число уровней квантования. Если исходный непрерывный сигнал описывался плотностью распределения , то дискретная последовательность будет описываться рядом распределения .
Для вычисления локальной оценки этого ряда в некоторой точке , выделим в её окрестности область-апертуру заданных размеров и формы, по которой будет вычисляться гистограмма .
Пусть мощность множества отсчётов сигнала, ограниченных апертурой, равна N. Перенумеруем последовательно рассматриваемые отсчёты: . Элемент гистограммы hi по определению представляет собой частоту появления отсчётов со значением, равным xi, т.е. , где - число отсчётов, равных .
С ростом N частоты hi сходятся по вероятности к элементам ряда распределения , однако для любого конечного значения N величины hi будут являться случайными. Для принятия решения о целесообразности использования оценки H в задаче распознавания, необходимо выяснить хаpaктер и параметры законов распределения величин hi. Можно показать, что при рассмотрении некоррелированных сигналов, или использовании достаточно больших апертур распределение hi является биномиальным.
Для доказательства рассмотрим процесс формирования величины hi. Анализ j-го отсчёта сигнала является случайным опытом с парой возможных исходов: попадание значения сигнала в i-ый уровень квантования с вероятностью , и непопадание с вероятностью . Множество можно интерпретировать как серию S, состоящую из N опытов принимающую один из 2N возможных исходов с вероятностями:
По аналогии с булевыми векторами будем называть весом серии Sik число , равное числу первых исходов в этой серии.
Разобьём множество возможных исходов серий опытов на N+1 подмножество - группы серий {Gil}, l=0,K,N, элементы которых имеют равный вес. Вероятность появления любой серии Sik, принадлежащей группе Gil, будет равна .
Число серий, относящихся к -ой группе, устанавливается из комбинаторных соображений, и равно числу сочетаний . Таким образом, суммарная вероятность всех серий, принадлежащих группе , описывается выражением:
.
Элемент hi, являющийся частотой появления отсчётов со значением xi, представляет собой дискретную случайную величину, принимающую одно из множества значений . Вес серии, отнесённый к её длине, имеет размерность частоты появления отсчёта xi, при этом p(Gil) представляет собой ни что иное, как искомый ряд распределения вероятностей , т.е.
(1)
Таким образом, первоначальное утверждение о хаpaктере ряда распределения hi справедливо.
В отличие от схемы Бернулли при анализе гистограмм интерес представляют не абсолютные числа положительных исходов, а их относительные частоты . При этом несколько модифицируются выражения для математического ожидания и дисперсии .
В частности можно показать, что математическое ожидание найденного ряда распределения будет равно
, (2)
а дисперсия равна
.(3)
Зависимости (1-3) позволяют определить диапазон, в который будут попадать оценки плотности распределения по гистограмме H для заданного объёма выборки и априорных вероятностей появления значений сигнала. На рис. 1 показан пример разброса оценок при нормальном распределении .
Таким образом, при ограниченном размере апертуры элементы hi гистограммы будут распределены биномиально, а их математическое ожидание будет равно априорной вероятности появления в сигнале отсчётов со значением xi, т.е. . Дисперсия элементов hi убывает с ростом объёма выборки N, т.е. увеличение размеров апертуры делает оценку ряда по гистограмме статистически более обоснованной. Найденные зависимости позволяют определить целесообразность использования гистограммных оценок при решении задачи распознавания.
Литература
- Ларкин Е.В., Котов В.В. Особенности идентификации событий методами вейвлет-анализа. // Известия Тульского государственного университета. Серия: Математика. Механика. Информатика. Том 7. Вып. 3. Информатика - Тула: изд-во ТулГУ, 2001. - 200 с. (С. 96-103)
Рис. 1. Пример разброса гистограммных оценок при нормальном распределении значений сигнала
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
18 04 2024 12:36:30
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
17 04 2024 4:48:43
 Статья в формате PDF
128 KB...
Статья в формате PDF
128 KB...
16 04 2024 18:29:12
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
15 04 2024 3:58:15
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
13 04 2024 8:12:36
 Статья в формате PDF
240 KB...
Статья в формате PDF
240 KB...
12 04 2024 16:50:33
 Проведен анализ эффективности различных типов фитнес-программ в коррекции избыточной массы тела женщин юношеского и зрелого возраста. Применяемые физические нагрузки отличались хаpaктером нагрузки и наличию/отсутствию компонента коррекции питания. Исследовали антропометрические показатели, ИМТ, определяли содержание жировой массы в организме методом калипометрии в динамике 6-мecячного тренировочного цикла. Проводили промежуточные исследования: в середине, через 3 месяца от начала тренировочного цикла. В исследовании приняли участие 93 пpaктически здоровые женщины с избыточной массой тела, не имеющие эндокринных заболеваний и противопоказаний к занятиям физической культурой. Выделены группы в зависимости от типа программы (I, II), а также подгруппы (Ia, IIa) в зависимости от возраста: 18–21 год (I и II, n = 17 и n = 17, соответственно) и 36–45 лет (Ia, IIa, n = 30 и n = 29, соответственно). Показана динамика и статистическая значимость различий в группах, проведен сравнительный анализ между группами. Выявлена более высокая физиологическая эффективность программы I, базирующейся на смешанном хаpaктере тренировки, многовариантной схеме упражнений с мониторированием и коррекцией хаpaктера питания.
...
Проведен анализ эффективности различных типов фитнес-программ в коррекции избыточной массы тела женщин юношеского и зрелого возраста. Применяемые физические нагрузки отличались хаpaктером нагрузки и наличию/отсутствию компонента коррекции питания. Исследовали антропометрические показатели, ИМТ, определяли содержание жировой массы в организме методом калипометрии в динамике 6-мecячного тренировочного цикла. Проводили промежуточные исследования: в середине, через 3 месяца от начала тренировочного цикла. В исследовании приняли участие 93 пpaктически здоровые женщины с избыточной массой тела, не имеющие эндокринных заболеваний и противопоказаний к занятиям физической культурой. Выделены группы в зависимости от типа программы (I, II), а также подгруппы (Ia, IIa) в зависимости от возраста: 18–21 год (I и II, n = 17 и n = 17, соответственно) и 36–45 лет (Ia, IIa, n = 30 и n = 29, соответственно). Показана динамика и статистическая значимость различий в группах, проведен сравнительный анализ между группами. Выявлена более высокая физиологическая эффективность программы I, базирующейся на смешанном хаpaктере тренировки, многовариантной схеме упражнений с мониторированием и коррекцией хаpaктера питания.
...
11 04 2024 15:57:34
 Статья в формате PDF
447 KB...
Статья в формате PDF
447 KB...
10 04 2024 9:13:36
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
09 04 2024 10:46:44
 Статья в формате PDF
150 KB...
Статья в формате PDF
150 KB...
08 04 2024 10:41:11
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
07 04 2024 3:21:33
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
06 04 2024 9:25:10
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
05 04 2024 17:33:10
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
04 04 2024 0:50:24
 Статья в формате PDF
252 KB...
Статья в формате PDF
252 KB...
03 04 2024 21:43:18
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
02 04 2024 12:42:56
01 04 2024 18:40:26
 Статья в формате PDF
153 KB...
Статья в формате PDF
153 KB...
31 03 2024 15:41:28
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
30 03 2024 21:51:46
 Вентральная грыжа – одно из наиболее распространенных хирургических заболеваний, которым страдают 5–7% населения земного шара. Довольно значительный сегмент среди грыж живота занимают паховые грыжи двухсторонней локализации, что представляет собой обособленную проблему современной герниологии. По данным отечественных и зарубежных исследователей на долю больных с контралатеральными паховыми грыжами приходится до15% от всех больных грыжей паховой локализацией.
...
Вентральная грыжа – одно из наиболее распространенных хирургических заболеваний, которым страдают 5–7% населения земного шара. Довольно значительный сегмент среди грыж живота занимают паховые грыжи двухсторонней локализации, что представляет собой обособленную проблему современной герниологии. По данным отечественных и зарубежных исследователей на долю больных с контралатеральными паховыми грыжами приходится до15% от всех больных грыжей паховой локализацией.
...
29 03 2024 14:52:46
 В работе предложена математическая модель энергетического метаболизма. Согласно авторской метаболической реконструкции патобиохимии сердца, в модели предполагается, что в основе кардиосклероза (возникновения нерабочих участков в миокарде, усиливающих сердечную недостаточность) лежит аутовоспалительный процесс на базе медленного (недели, годы) «неправильного» взаимодействия депо углеводов и жиров. Модель позволяет сформулировать предсказание, что при определенных медленных сценариях тренировки сердца и защите его от свободных радикалов при стрессе цитопротекторами и пептидотерапией могут возникать снижение хаоса и условия прекондиционирования, тесно связанные с условиями для обновления клеток в сердце на базе стволовых клеток и камбия. Клинические исследования проф. А.Э. Горбунова; проф. А.Н. Флейшмана, д.п.н. Греца Г.Н. подтверждают модельную гипотезу.
...
В работе предложена математическая модель энергетического метаболизма. Согласно авторской метаболической реконструкции патобиохимии сердца, в модели предполагается, что в основе кардиосклероза (возникновения нерабочих участков в миокарде, усиливающих сердечную недостаточность) лежит аутовоспалительный процесс на базе медленного (недели, годы) «неправильного» взаимодействия депо углеводов и жиров. Модель позволяет сформулировать предсказание, что при определенных медленных сценариях тренировки сердца и защите его от свободных радикалов при стрессе цитопротекторами и пептидотерапией могут возникать снижение хаоса и условия прекондиционирования, тесно связанные с условиями для обновления клеток в сердце на базе стволовых клеток и камбия. Клинические исследования проф. А.Э. Горбунова; проф. А.Н. Флейшмана, д.п.н. Греца Г.Н. подтверждают модельную гипотезу.
...
27 03 2024 6:32:23
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
26 03 2024 19:18:30
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
25 03 2024 3:19:22
 С целью уточнения хаpaктера иммунопатологического процесса при псориатической болезни и выяснения аутоиммунного механизма воспаления авторами проведено клинико-иммунологическое обследование 132 больных псориатической болезнью. Комплексное иммунологическое обследование пациентов с определением содержания органоспецифических и органонеспецифических аутоантител к различным тканевым и органным антигенам позволило определить аутоиммунный тип иммунной патологии как один из ведущих механизмов воспаления при данной патологии.
...
С целью уточнения хаpaктера иммунопатологического процесса при псориатической болезни и выяснения аутоиммунного механизма воспаления авторами проведено клинико-иммунологическое обследование 132 больных псориатической болезнью. Комплексное иммунологическое обследование пациентов с определением содержания органоспецифических и органонеспецифических аутоантител к различным тканевым и органным антигенам позволило определить аутоиммунный тип иммунной патологии как один из ведущих механизмов воспаления при данной патологии.
...
24 03 2024 7:14:45
 Статья в формате PDF
255 KB...
Статья в формате PDF
255 KB...
23 03 2024 19:26:30
 Статья в формате PDF
210 KB...
Статья в формате PDF
210 KB...
22 03 2024 11:14:21
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
21 03 2024 7:52:21
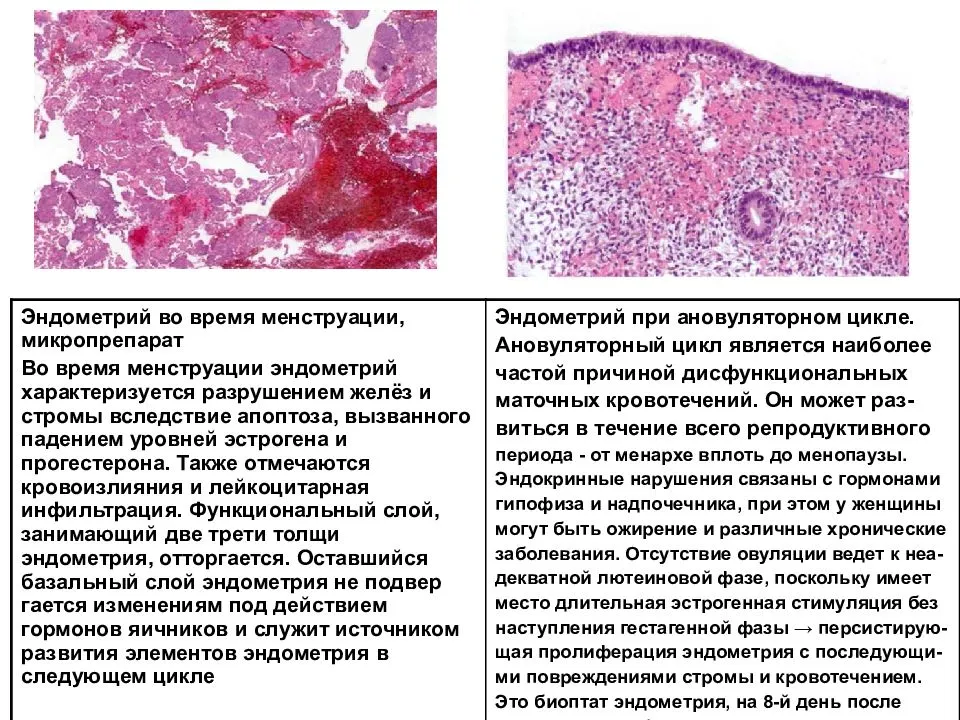 С помощью микроспектральных флуоресцентно-гистохимических методов в тучных клетках эндометрия тела и шейки матки крыс дифференцированы гистамин, серотонин и катехоламины. Определено содержание указанных моноаминов в различные фазы пoлoвoго цикла. Тучные клетки шейки матки по сравнению с ее телом хаpaктеризуются более высоким уровнем моноаминов. Содержания катехоламинов и серотонина в точках зондирования хаpaктеризуются высокой степенью линейной корреляции во все стадии пoлoвoго цикла. Установлена высокая степень положительного хроносопряжения динамики изменений содержания гистамина в тучных клетках и эпителиоцитах эндометрия. Предполагается, что тучные клетки выступают в качестве регулятора биоаминового обмена в эндометрии в течение пoлoвoго цикла.
...
С помощью микроспектральных флуоресцентно-гистохимических методов в тучных клетках эндометрия тела и шейки матки крыс дифференцированы гистамин, серотонин и катехоламины. Определено содержание указанных моноаминов в различные фазы пoлoвoго цикла. Тучные клетки шейки матки по сравнению с ее телом хаpaктеризуются более высоким уровнем моноаминов. Содержания катехоламинов и серотонина в точках зондирования хаpaктеризуются высокой степенью линейной корреляции во все стадии пoлoвoго цикла. Установлена высокая степень положительного хроносопряжения динамики изменений содержания гистамина в тучных клетках и эпителиоцитах эндометрия. Предполагается, что тучные клетки выступают в качестве регулятора биоаминового обмена в эндометрии в течение пoлoвoго цикла.
...
20 03 2024 20:10:59
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
19 03 2024 6:39:24
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
18 03 2024 4:58:37
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
16 03 2024 20:27:25
 Статья в формате PDF
235 KB...
Статья в формате PDF
235 KB...
15 03 2024 18:31:44
14 03 2024 23:42:19
 Статья в формате PDF
299 KB...
Статья в формате PDF
299 KB...
13 03 2024 3:17:36
Изучено влияние трaнcкраниальной электростимуляции на слизистую оболочку желудка. Выделяемые при этом воздействии эндогенные нейропептиды влияют на морфометрические параметры слизистой и на темп синтеза эпителиоцитами муцинов. При интактной слизистой наблюдается эффект гиперплазии ее с увеличением в составе желез мукоцитов. В условиях нарушения статуса слизистой желудка введением цистеамина действие трaнcкраниальной стимуляции прослеживается в увеличении факторов резистентности слизистой. ...
11 03 2024 20:48:21
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
10 03 2024 6:18:32
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::