КЛАСТЕРНЫЙ АНАЛИЗ В СТРУКТУРЕ ИНФОРМАТИЗАЦИИ ДИДАКТИЧЕСКОГО ПРОЦЕССА
Введение
Интеграция педагогических и информационных технологий - одна из тенденций развития педагогической науки и пpaктики. Известно, что технология хаpaктеризуется тремя аспектами - информационным, инструментальным и социальным. Анализ научно-методической литературы и педагогической пpaктики показал, что в настоящее время недостаточно разработан информационный аспект педагогических информационных технологий, т.е. методы обработки информации в педагогическом управлении. По-прежнему в большинстве случаев и прогнозирование учебных достижений обучающихся, и принятие педагогических решений для коррекции дидактического процесса происходит умозрительно. Проблема исследования заключается в вопросе: какие математические методы обработки информации позволят автоматизировать прогнозирование учебных достижений обучающихся и принятие педагогических решений? Цель исследования - изучить роль кластерного анализа данных в процессе интеграции педагогических и информационных технологий.
Методы исследования
Под кластерным анализом понимают разбиение совокупности объектов на непересекающиеся подмножества (кластеры) с целью выделения групп схожих объектов. Кластеризация возможна как по количественным параметрам, так и качественным.
Результаты исследования
С точки зрения авторов, научно обоснованное прогнозирование учебных достижений обучающихся и принятие точных педагогических решений возможно только на основе кластеризации обучающихся. Ее следует производить на основе количественных показателей, отражающих как результаты учебной деятельности обучающихся, так и ее факторы (их можно получить в результате пропедевтического контроля и т.д.).
Ранее авторами статьи была разработана методика матричного моделирования сложных педагогических систем, основанная на получении матрицы вероятностей взаимосвязи между переменной-фактором и переменной-откликом. Обобщим данную методику.
Пусть S - набор прогнозируемых параметров (т.е. результатов учебной деятельности обучающихся), К - множество обучающихся. Тогда (при этом ), где N - число кластеров (групп обучающихся, схожих по выбранным параметрам). Необходимо помнить, что педагог может проводить дидактический процесс в нескольких учебных или академических группах. В этом случае , где L - количество учебных (академических) групп, Gi - множество обучающихся в I-й группе. Очевидно, что следует различать академические и кластерные группы. Например, обучающиеся одной кластерной группы могут принадлежать различным академическим группам (и наоборот).
По своей сути, S - многомерный вектор прогнозируемых параметров (D - их число, или размерность вектора). Для каждого параметра Si ( ) производят разбиение диапазона его возможных значений на непересекающиеся поддиапазоны. Множество числовых значений каждого поддиапазона принимают за квантованное значение переменной Si. Тогда конкретное значение многомерного вектора S составит комбинация квантованных значений составляющих его переменных.
Формируют матрицу вероятности, строками которой являются кластеры обучающихся, столбцами - комбинация прогнозируемых параметров для кластера. Пересечение строки и столбца отражает вероятность того, что для I-й кластерной группы набор прогнозируемых параметров примет j-е значение (обозначим ). Очевидно, что . Информационная энтропия (неопределенность) прогноза для I-го кластера .
Основные факторы уменьшения энтропии прогноза - сужение кластеров (это означает увеличение их количества) и сбор как можно большего объема информации о поведении объектах, относящихся к данному кластеру (информацию об обучающихся, факторах и результатах их учебной деятельности следует хранить в базе данных).
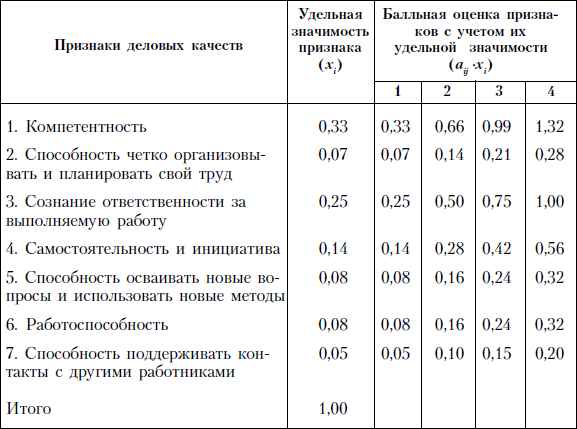
Возникает первый вопрос: каким образом формировать кластерные группы, т.е. выделять схожие объекты? Предложенный алгоритм состоит в следующем. Выделяют набор переменных W (пусть их число равно Q), по которым будут производить кластеризацию обучающихся (может не совпадать с S). Значения всех переменных путем расчетов преобразуют в условные баллы по R-балльной шкале (методы такого преобразования ранее были описаны авторами). Пусть εi - значимость (вес) I-го показателя ( ), при этом . Тогда расстояние в фазовом прострaнcтве (прострaнcтве признаков) между обучающимся (1) и обучающимся (2) составит , где и - соответственно значение (в баллах) I-го параметра для обучающегося (1) и обучающегося (2). Данных обучающихся относят к одному кластеру, если , где Δ - наперед заданное число, зависящее от рода задачи и необходимой точности ее решения.
Возникает второй вопрос: какие переменные следует отбирать во множество W - латентные (т.е. интегральные показатели) или индикаторные (т.е. дифференциальные показатели)? Ответ на данный вопрос во многом зависит от рода задачи, но в большинстве случаев, безусловно, более целесообразно применение интегральных параметров. В теории и пpaктике физического воспитания это могут быть физические качества (сила, быстрота, гибкость, выносливость и ловкость), здоровье, мотивация к занятиям физической культурой и т.д. В профессиональном образовании это может быть обученность, компоненты профессиональной компетентности будущего специалиста и т.д.
Аналогичным образом применяют кластерный анализ при принятии педагогических решений. Для каждого кластера обучающихся педагог в процессе своей деятельности (зачастую многолетней) отбирает наиболее рациональные варианты принятых решений, накапливая их в базе знаний (разновидность базы данных). Это позволяет сократить время на принятие верных педагогических решений и сделать данный процесс оперативным.
Кластерный анализ позволит существенно улучшить проведение педагогического эксперимента (включая обработку его результатов). При этом контрольную и экспериментальную группы можно разбить на кластеры, для каждого из которых следует вычислять эффективность апробируемой педагогической технологии в соответствии с общеизвестной схемой ROXO. Это позволит выявить условия эффективности апробируемой технологии (для одних кластеров она может оказаться эффективной, для других - нет).
Следует отметить, что применение кластерного анализа в обучении (управлении процессом усвоения знаний) и физическом воспитании (управлении процессом физического развития) во многом сходны между собой. Наиболее существенное отличие состоит в том, что в теории, методике и пpaктике физического воспитания приходится учитывать, помимо количественных параметров, качественные показатели (например, пoлoвые особенности, наличие или отсутствие заболеваний и т.д.). В этом случае производят предварительное разбиение множества обучающихся на подмножества по качественным показателям, а образовавшиеся подмножества подвергают кластерному анализу по количественным параметрам.
Заключение
Применение математических методов обработки информации - необходимое условие выведения научно-методической и педагогической деятельности на новый уровень. Кластерный анализ должен стать неотъемлемым компонентом методической системы математизации и информатизации педагогической науки и пpaктики. Пpaктическое значение кластерного анализа состоит в том, что его применение позволит оптимально совместить фронтальный и индивидуальный подходы к обучающимся.
Статья в формате PDF
111 KB...
26 04 2024 20:28:37
Статья в формате PDF
118 KB...
24 04 2024 14:29:39
На основе анализа литературных источников показана необходимость создания эффективных методов переработки руд цветных металлов. Описано отрицательное воздействие горнообогатительного производства на окружающую среду. Рассмотрены проблемы освоения месторождений сырья и предложены пути их решения. Приведена схема рационального освоения минеральных ресурсов рудного месторождения с применением разрядноимпульсных методов. Обоснована возможность использования разрядноимпульсных воздействий в обогатительных процессах, что позволит повысить полноту извлечения полезных компонентов при переработке минерального сырья. Выделены ограничения применения импульсных методов. Установлено, что разрядноимпульсные методы интенсифицируют избирательное раскрытие минеральных ассоциаций во всем диапазоне исходных классов крупности. Эти методы эффективны в комбинированных схемах переработки труднообогатимых руд сложного состава. Применение комбинированных схем позволит сократить на 10–15 % время измельчения до выхода контрольного класса.
...
23 04 2024 23:26:21
Важность разработки и внедрения системы менеджмента качества в вузе отражена и закреплена в ряде приказов Федерального агентства по образованию и обусловлена предстоящим вступлением страны в ВТО и присоединение к Болонскому процессу. В статье описываются алгоритм, этапы деятельности, результаты разработки и внедрения СМК в Кузбасском государственном техническом университете.
...
21 04 2024 13:46:53
Статья в формате PDF
106 KB...
20 04 2024 5:43:32
Статья в формате PDF
294 KB...
19 04 2024 15:50:18
Статья в формате PDF
253 KB...
18 04 2024 12:29:23
Статья в формате PDF
100 KB...
17 04 2024 10:20:40
Статья в формате PDF
145 KB...
15 04 2024 14:56:16
Статья в формате PDF
278 KB...
14 04 2024 13:37:52
Статья в формате PDF
109 KB...
12 04 2024 0:25:13
Статья в формате PDF
260 KB...
10 04 2024 13:52:38
Статья в формате PDF
107 KB...
09 04 2024 20:44:41
Статья в формате PDF
105 KB...
07 04 2024 7:21:51
Статья в формате PDF
100 KB...
06 04 2024 3:53:50
Статья в формате PDF
146 KB...
05 04 2024 6:20:18
Статья в формате PDF
102 KB...
03 04 2024 11:17:17
Статья в формате PDF
131 KB...
02 04 2024 1:16:40
Повышение уровня свинца в крови у детей дошкольного возраста на 1 мкг/дл ведет к снижению интеллектуального развития ребенка на 1/4–1/2 балла, причем негативные последствия обнаруживаются и через 10 лет после воздействия свинца в раннем возрасте. Целью данного исследования было дать гигиеническую оценку загрязнения почвы в качестве депонирующей системы свинцом в городе Шымкент. Для исследования почвы на содержание свинца был произведен забор проб согласно ГОСТу 17.4.02-84. Определение свинца проводили на атомно-абсорбционном спектрометре МГА-915 с электротермической атомизацией. В результате исследования установлено превышение содержания свинца в почве по отношению к ПДК во всех отобранных пробах. Причем, по мере удаления от завода концентрация свинца в почве хотя и уменьшалось, но превышало ПДК в 3–4 раза. При исследовании овощей произрастающих на загрязненной территории, максимальное содержание свинца установлено в картофеле (в среднем 3 ПДК в 1 зоне). Таким образом, полученные результаты показали, что наибольшее загрязнение наблюдается на расстоянии 500–1000 м от завода. Вместе с тем обнаружено загрязнение почвы по всей изучаемой территории, где складывается нeблагоприятная санитарная ситуация по свинцу.
...
01 04 2024 12:13:19
Статья в формате PDF
128 KB...
31 03 2024 19:48:34
Одной из важнейших проблем современной перинатологии является прогрессирующий рост инфекционной патологии у плода и новорожденного. Целью данной работы являлась комплексная ультразвуковая оценка фето-плацентарной системы у беременных с высоким инфекционным индексом для прогнозирования степени тяжести внутриутробного инфицирования у новорожденного.
Обследовано 123 беременных в сроке гестации 30-36 недель. В зависимости от тяжести состояния все новорожденные ретроспективно были разделены на 4 группы. В контрольную (1 группа) вошли новорожденные от матерей с неосложненной беременностью, состояние ребенка при рождении удовлетворительное. В основную (1 – 4 группы) вошли новорожденные от матерей с высоким инфекционным индексом, с локальными или генерализованными проявлениями внутриутробной инфекции.
В результате проведенного исследования выявлены эхографические маркеры амнионита, плацентита и собственно инфекционного поражения плода, которое наиболее значимо для прогнозирования рождения ребенка с ВУИ.
Патологические показатели биофизической активности, допплерометрия отражают системные нарушения в состоянии плода, его дисстресс.
Таким образом, чем больше эхографических маркеров внутриутробного инфицирования встречается у плода, тем более вероятно рождение ребенка с признаками ВУИ.
...
30 03 2024 9:56:50
Статья в формате PDF
359 KB...
27 03 2024 20:39:28
Статья в формате PDF
153 KB...
25 03 2024 9:52:10
Статья в формате PDF
355 KB...
24 03 2024 13:38:25
Статья в формате PDF
254 KB...
23 03 2024 0:32:21
Статья в формате PDF
125 KB...
22 03 2024 4:30:35
Статья в формате PDF
210 KB...
20 03 2024 23:44:21
Статья в формате PDF
100 KB...
19 03 2024 15:33:10
Статья в формате PDF
123 KB...
18 03 2024 18:44:13
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
