ОБ АСИМПТОТИКЕ ОЦЕНКИ ПОГРЕШНОСТИ МЕТОДА ПРОСТЫХ ИТЕРАЦИЙ
В работе рассматривается асимптотическое представление оценки вектора ошибки метода простых итераций. Такое представление обеспечивает явный вид оценки погрешности итерационного процесса, что может быть полезным при построении алгоритмов, реализующих неявные вычислительные схемы одношаговых методов решения алгебро-дифференциальных систем уравнений в сочетании с методом простых итераций и определения априорного числа итераций.
Объектом исследования является рекуррентное равенство x(k) = F(x( k - 1)), k = 0, 1, 2, ... определяющее метод простых итераций (метод последовательных приближений) [1], [2] и, при некотором заданным начальном векторе x(0), обеспечивающее возможность построения итерационного процесса для нахождения решения системы нелинейных алгебраических уравнений, приведенных к виду:
x = F(x), (1)
где F - векторная функция векторного аргумента x, x∈Rl, F: D ⊂ Rl → Rl.
Будем предполагать, что для уравнения (1) выполнены условия теоремы о существовании и единственности решения [1, с. 401] и верно выражение для оценки нормы вектора погрешности:
|| x* - x( k) || ≤ t* - tk, (2)
где tk = 0.5γ t2k -1 + δ tk -1 + η, t0 = 0.
Целью работы является получение выражения явной зависимости оценки погрешности (2), от параметров α, δ и числа итераций k.
Утверждение. В методе простых итераций оценка вектора погрешности определяется неравенством:
где α - малая величина, M - const.
СПИСОК ЛИТЕРАТУРЫ:
- Ортега Д., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими переменными. М.: Мир, 1975. - 558 с.
- Канторович Л.В., Акилов Г.П. Функциональный анализ. М.: Наука, 1977. -741 с.
- Ацел Я., Дембр Ж. Функциональные уравнения с несколькими переменными. М.: ФИЗМАТЛИТ, 2003. - 432 с.
Представлены результаты исследований влияния открытых разработок месторождений золота на почвенный покров Якокит – Селигдарского междуречья Южной Якутии. Изучены разновозрастные дражные отвалы и почвы естественных лесных биогеоценозов. Главная особенность дражных полигонов – отсутствие или незначительное количество мелкоземного субстрата на отвалах. Мелкоземный субстрат отвалов беден элементами питания. Регенерация почвенного покрова на техногенных ландшафтах затруднена и часто не происходит.
...
27 04 2024 8:57:20
Статья в формате PDF
559 KB...
26 04 2024 2:38:48
Статья в формате PDF
106 KB...
25 04 2024 22:50:42
Построена октетная электродинамика. Обсуждена возможность объединения механики и электродинамики. Выявлена дальнодействующая структуризация октетного прострaнcтва. Исследуются свойства интервала.
...
24 04 2024 6:23:17
Статья в формате PDF
106 KB...
22 04 2024 18:52:20
Статья в формате PDF
103 KB...
21 04 2024 16:41:32
По комплексу признаков оценили трaнcформированные урбанизацией лесные фитоценозы, и населяющие их сообщества мелких млекопитающих в лесопарково-парковой зоне крупного промышленного центра. Выявили, что хотя и наблюдаются общие закономерности в группировке фито- и зооценозов в зависимости от уровня и хаpaктера урбаногенного воздействия, но между ними нет полного соответствия. Специфика сообществ мелких млекопитающих определяется не только эдафо-растительными условиями. Ведущим параметром в трaнcформации сообществ является рекреация и сопровождающие ее факторы.
...
19 04 2024 20:59:40
Статья в формате PDF
163 KB...
18 04 2024 3:24:22
Статья в формате PDF
97 KB...
17 04 2024 0:49:27
Статья в формате PDF
268 KB...
14 04 2024 19:18:38
Статья в формате PDF
146 KB...
13 04 2024 8:38:32
Статья в формате PDF
116 KB...
12 04 2024 2:31:10
Статья в формате PDF
295 KB...
11 04 2024 8:38:31
Статья в формате PDF
254 KB...
10 04 2024 0:37:17
Статья в формате PDF
103 KB...
09 04 2024 20:17:12
Статья в формате PDF
125 KB...
08 04 2024 2:27:19
Статья в формате PDF
113 KB...
07 04 2024 22:18:46
Статья в формате PDF
1797 KB...
06 04 2024 10:53:19
Статья в формате PDF
111 KB...
05 04 2024 19:22:14
Рассматривается проблема организации продуктивной умственной деятельности учащихся общеобразовательных учреждений в системе дидактических принципов современной педагогики. Анализ принципов показывает, что отечественная дидактика в большой мере сохраняет черты традиционной модели обучения и недостаточно учитывает психологическую природу мышления и закономерности продуктивной умственной деятельности при разработке принципов обучения. Выделены основополагающие принципы организации продуктивной умственной деятельности на основе закономерностей развития знания и процесса познания, психологических закономерностей мышления.
...
04 04 2024 0:21:55
Статья в формате PDF
276 KB...
03 04 2024 19:52:20
Статья в формате PDF
132 KB...
02 04 2024 19:42:40
Статья в формате PDF
121 KB...
01 04 2024 16:51:47
Статья в формате PDF
101 KB...
31 03 2024 13:14:33
Статья в формате PDF
139 KB...
30 03 2024 18:43:57
Статья в формате PDF
148 KB...
29 03 2024 23:18:53
Статья в формате PDF
112 KB...
28 03 2024 4:16:19
Статья в формате PDF
276 KB...
27 03 2024 8:37:56
Статья в формате PDF
102 KB...
26 03 2024 8:22:36
Статья в формате PDF
103 KB...
24 03 2024 12:15:13
Рассмотрен вариант синхронного деления клеток. Предложены кинетические уравнения, описывающие рост, размножение и гибель микроорганизмов с учетом как естественной cмepтности, так и внутривидовой борьбы. Рассматривается квазистационарный метод решения уравнения для определения плотности функции распределения микроорганизмов по возрастам. Предложен явный вид коэффициента диффузии в прострaнcтве масс. Получено аналитическое решение в квазистационарном приближении для плотности функции распределения микроорганизмов по возрастам для случая, когда рост клетки пропорционален ее массе (объему).
...
23 03 2024 6:22:35
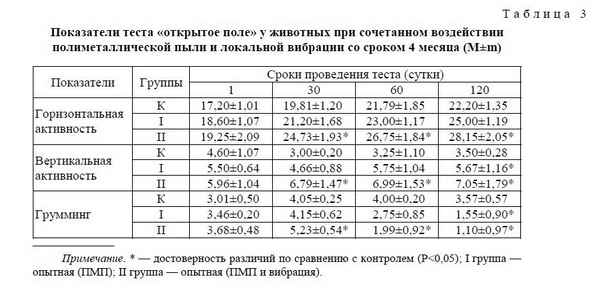Целью настоящего исследования явилось изучение показателей перекиcного окисления липидов в гомогенатах печени, почек и легких крыс в динамике ингаляционного воздействия полиметаллической пылью, содержащей естественные радионуклиды.
Полученные нами данные показали, что при пролонгированном ингаляционном поступлении полиметаллической пыли, содержащей природные радионуклиды, в легких, печени и почках крыс происходит активация процессов ПОЛ. Обращает на себя внимание разные сроки начала аккумуляции катаболитов ПОЛ: в легких – на 7 сутки, в печени и почках – на 30 сутки. Выявление хаpaктера нарушений окислительного метаболизма доказывают необходимость ранней коррекции нарушения окислительного метаболизма при пролонгированной экспозиции полиметаллической пыли, содержащей природные радионуклиды.
...
22 03 2024 22:23:57
Статья в формате PDF
273 KB...
21 03 2024 6:27:39
Статья в формате PDF
112 KB...
19 03 2024 0:29:18
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
