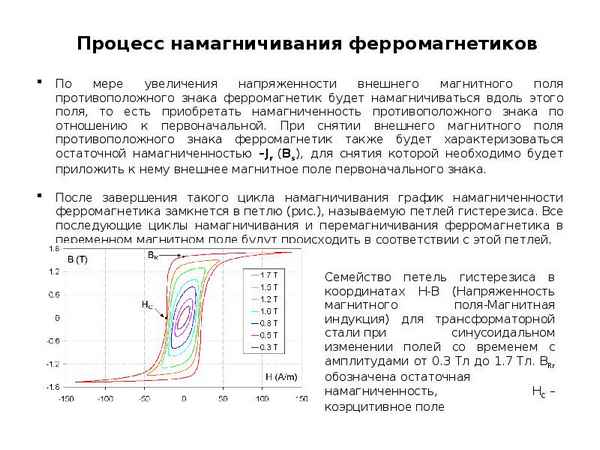
ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ ФИЗИКО-ХИМИЧЕСКИХ ПРОЦЕССОВ ВОСПЛАМЕНЕНИЯ РЕАГИРУЮЩЕЙ КОНДЕНСИРОВАННОЙ СРЕДЫ

Известные математические модели процессов воспламенения и горения реагирующих сред основаны на рассмотрении сопряженных теплофизических и термокинетических явлений в пограничном слое. При этом, основными механизмами реализации данных процессов являются составляющие конвективного и диффузионного переноса тепловой энергии (энтальпии) в среде с учетом неравновесных источников внутреннего тепловыделения и химической кинетики. Уточнение физической сущности процессов теплопроводности и химической кинетики, определяющих явления воспламенения и горения реагирующих конденсированных сред (РКС), представляется одним из наиболее сложных разделов аналитической и вычислительной тепломеханики и термохимии.
Предложен дивергентный вид системы одномерных дифференциальных уравнений в частных производных, определяющих хаpaктеристики процессов теплопереноса и химической кинетики n-го порядка в пограничном слое РКС:
(1)
где A(x,t), B(x,t), C(x,t) - векторы-столбцы искомых функций состояния, составляющих переноса и активности внутренних источников.
Ω (x,t) - функция скорости реакции в источнике (кинетический множитель Аррениуса).
В основе существующих математических схем и аппроксимаций системы уравнений (1) положены различные варианты метода конечных разностей: алгоритмов явной схемы «предиктор-корректор», явной схемы Адамса - Бэшфорта и неявной итерационной схемы.
В результате проведенного анализа особенностей получаемых решений было выявлено, что явные схемы не обеспечивают необходимой устойчивости решения в окрестности точки перехода от режима инертного прогрева к воспламенению, что частично устраняется введением дополнительных сглаживающих процедур и значительным снижением шага интегрирования. Для реализаций неявных схем, данное сглаживание является избыточным (проявляются известные диффузионные свойства неявных аппроксимаций), что также негативно сказывается на точности получаемых решений.
Предложена схема вычислительного решения системы неоднородных уравнений (1), использующая метод расщепления. Вычислительный цикл схемы включает три последовательно выполняемых этапа внутри единичного шага по времени.
1. На данном этапе изменяются величины Tin и βin , относящиеся непосредственно к i-ой ячейке - составляющих компонентов векторов А и С (1), без учета потоков конвективного и диффузионного переноса. Внутреннее тепловое состояние ячейки является замороженным:
(2)
2. На данном этапе проводится вычисление эффектов переноса - составляющих компонентов вектора B (1), учитывающих обмен между ячейками (i; i+1) и (i-1; i):
(3)
(4)
где
3. Здесь происходит перераспределение тепловой энергии в прострaнcтве реагирующей среды в момент времени tn+1. На новом временном слое, исходные уравнения аппроксимируются следующим образом:
(5)
Компоненты векторов В и С определяются с учетом решений первого этапа (2).
Проведены исследования и показана сходимость схемы решения (2-5) уравнений (1) для широкого диапазона краевых условий процессов воспламенения и горения РКС.
25 04 2024 2:10:41
 Статья в формате PDF
141 KB...
Статья в формате PDF
141 KB...
24 04 2024 10:24:52
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
23 04 2024 20:37:13
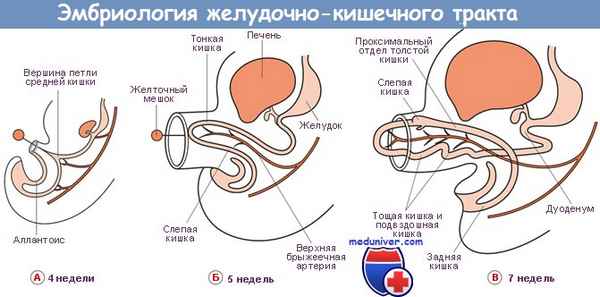 Закладка двенадцатиперстной кишки имеет форму короткой дуги, она преобразуется в полукольцо при поперечном положении на рубеже 6-й – 7-й недель эмбриогенеза человека. У плодов эти состояния встречаются редко.
...
Закладка двенадцатиперстной кишки имеет форму короткой дуги, она преобразуется в полукольцо при поперечном положении на рубеже 6-й – 7-й недель эмбриогенеза человека. У плодов эти состояния встречаются редко.
...
22 04 2024 13:24:27
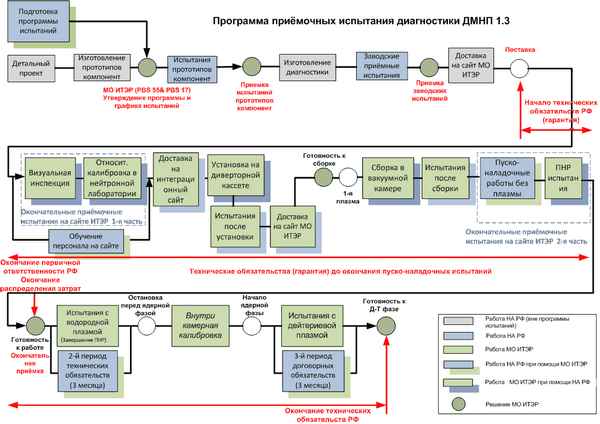 Разработан пакет графических алгоритмических моделей отбpaковочных испытаний радиоприемных устройств, изготавливаемых и выпускаемых предприятием, как первый шаг к последующей автоматизации. Показано преимущество разработанных моделей по сравнению с действующей текстовой инструкцией по проведению испытаний.
...
Разработан пакет графических алгоритмических моделей отбpaковочных испытаний радиоприемных устройств, изготавливаемых и выпускаемых предприятием, как первый шаг к последующей автоматизации. Показано преимущество разработанных моделей по сравнению с действующей текстовой инструкцией по проведению испытаний.
...
21 04 2024 14:23:24
20 04 2024 13:14:46
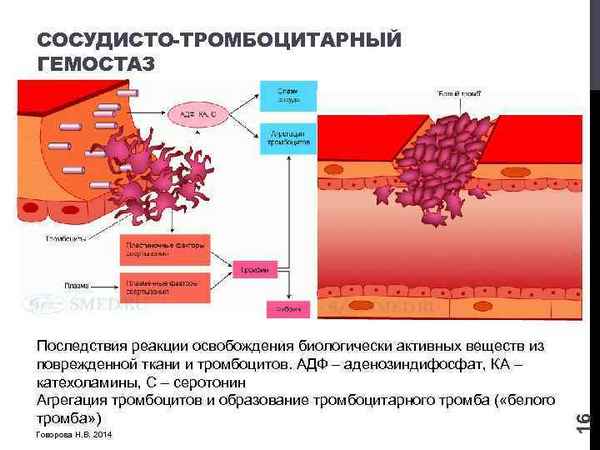 Активация лейкоцитов и тромбоцитов циркулирующей крови детей при неотложных состояниях сопровождается интенсификацией образования в ней клеточных ассоциаций, представленных ауторозетками, образованными лейкоцитами из эритроцитов, и тромбоцитарными агрегатами. Циркуляция в крови значительных количеств этих клеточных ассоциаций способна вызвать ухудшение её реологических свойств и соответственно нарушения микроциркуляции. Поскольку эритроциты, входящие в состав ауторозеток и контактирующие с тромбоцитами, подвергаются экзоцитарному лизису, это приводит к поступлению в циркулирующую кровь эритроцитарных прокоагулянтов и увеличивает возможность тромбообразования. Поэтому интенсификацию образования ауторозеток и тромбоцитарных агрегатов можно рассматривать как патогенетические факторы нарушений микроциркуляции при неотложных состояниях.
...
Активация лейкоцитов и тромбоцитов циркулирующей крови детей при неотложных состояниях сопровождается интенсификацией образования в ней клеточных ассоциаций, представленных ауторозетками, образованными лейкоцитами из эритроцитов, и тромбоцитарными агрегатами. Циркуляция в крови значительных количеств этих клеточных ассоциаций способна вызвать ухудшение её реологических свойств и соответственно нарушения микроциркуляции. Поскольку эритроциты, входящие в состав ауторозеток и контактирующие с тромбоцитами, подвергаются экзоцитарному лизису, это приводит к поступлению в циркулирующую кровь эритроцитарных прокоагулянтов и увеличивает возможность тромбообразования. Поэтому интенсификацию образования ауторозеток и тромбоцитарных агрегатов можно рассматривать как патогенетические факторы нарушений микроциркуляции при неотложных состояниях.
...
19 04 2024 15:24:41
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
16 04 2024 3:10:23
15 04 2024 17:16:19
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
14 04 2024 0:23:10
12 04 2024 18:16:55
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
09 04 2024 3:38:50
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
08 04 2024 21:11:53
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
07 04 2024 14:47:18
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
06 04 2024 17:38:55
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
05 04 2024 8:52:27
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
04 04 2024 1:56:49
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
03 04 2024 14:47:51
 Статья в формате PDF
249 KB...
Статья в формате PDF
249 KB...
02 04 2024 18:17:30
 Статья в формате PDF
301 KB...
Статья в формате PDF
301 KB...
01 04 2024 0:13:49
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
31 03 2024 2:24:47
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
30 03 2024 10:53:47
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
29 03 2024 7:16:42
 Статья в формате PDF
143 KB...
Статья в формате PDF
143 KB...
28 03 2024 11:21:44
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
27 03 2024 11:19:30
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
25 03 2024 19:30:30
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
24 03 2024 7:18:53
 Статья в формате PDF
276 KB...
Статья в формате PDF
276 KB...
23 03 2024 11:47:12
 Статья в формате PDF
779 KB...
Статья в формате PDF
779 KB...
21 03 2024 3:12:54
 В работе рассматривается процесс утилизации ртутьсодержащих соединений с использованием в качестве активного соединения кремния, что экономически более выгодно, чем использование порошкообразного титана. Рассматривается возможность миграции ртути в условиях возрастающей техногенной деятельности человечества.
...
В работе рассматривается процесс утилизации ртутьсодержащих соединений с использованием в качестве активного соединения кремния, что экономически более выгодно, чем использование порошкообразного титана. Рассматривается возможность миграции ртути в условиях возрастающей техногенной деятельности человечества.
...
20 03 2024 22:30:59
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
19 03 2024 16:48:59
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
17 03 2024 13:37:44
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::