ПАТТЕРНЫ ВНУТРИ ПАТТЕРНОВ

Причина, по которой мы затеяли этот экскурс в историю комплексных чисел, заключается в том, что многие фpaктальные формы могут быть воспроизведены математически, с помощью итеративных процедур на комплексной плоскости. В конце 70-х годов, опубликовав свою новаторскую книгу, Maндельбро обратил внимание на особый класс математических фpaкталов, известных как множество Жулиа [1]. Эти множества были открыты французским математиком Гастоном Жулиа в начале XX столетия, но скоро канули в безвестность.
В основу множества Жулиа положено простое отображение:
z → z2 + c, (1)
где z - комплексная переменная, а с - комплексная постоянная. Итеративная процеДypa состоит в выборе любого комплексного числа z на комплексной плоскости, возведении его в квадрат, добавления константы с, возведении результата в квадрат, добавления к нему константы с и т. п.. Когда эти вычисления выполняются с различными начальными значениями z, некоторые из них будут увеличиваться до бесконечности в ходе процесса итерации, в то время как другие остаются конечными [2]. Множество Жулиа - это набор всех тех значений z, которые при итерации ограничены некоторым пределом, т.е. конечны.
Чтобы определить тип множества Жулиа для определенной константы с, итерацию необходимо каждый раз выполнить для нескольких тысяч точек, пока не выяснится, продолжают ли значения увеличиваться или остаются конечными. Если конечные точки помечать черным цветом, а те, что продолжают увеличиваться, - белым, множество Жулиа проявится в виде черной фигуры.
СПИСОК ЛИТЕРАТУРЫ:
- Mandelbrot B.B. The Fractial Geometry of Nature. //N.Y.: «Freeman». 1983. s. 335.
- Mander J. In Absence of the Sacred. // S.F.: «Sierra Club Books». 1991. s. 521.
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
17 04 2024 7:47:37
 Статья в формате PDF
285 KB...
Статья в формате PDF
285 KB...
16 04 2024 10:45:28
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
15 04 2024 3:48:45
 Статья в формате PDF
204 KB...
Статья в формате PDF
204 KB...
14 04 2024 15:53:27
 Статья в формате PDF
322 KB...
Статья в формате PDF
322 KB...
13 04 2024 20:37:30
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
12 04 2024 14:30:11
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
11 04 2024 22:27:42
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
10 04 2024 0:29:41
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
09 04 2024 7:29:21
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
08 04 2024 14:11:11
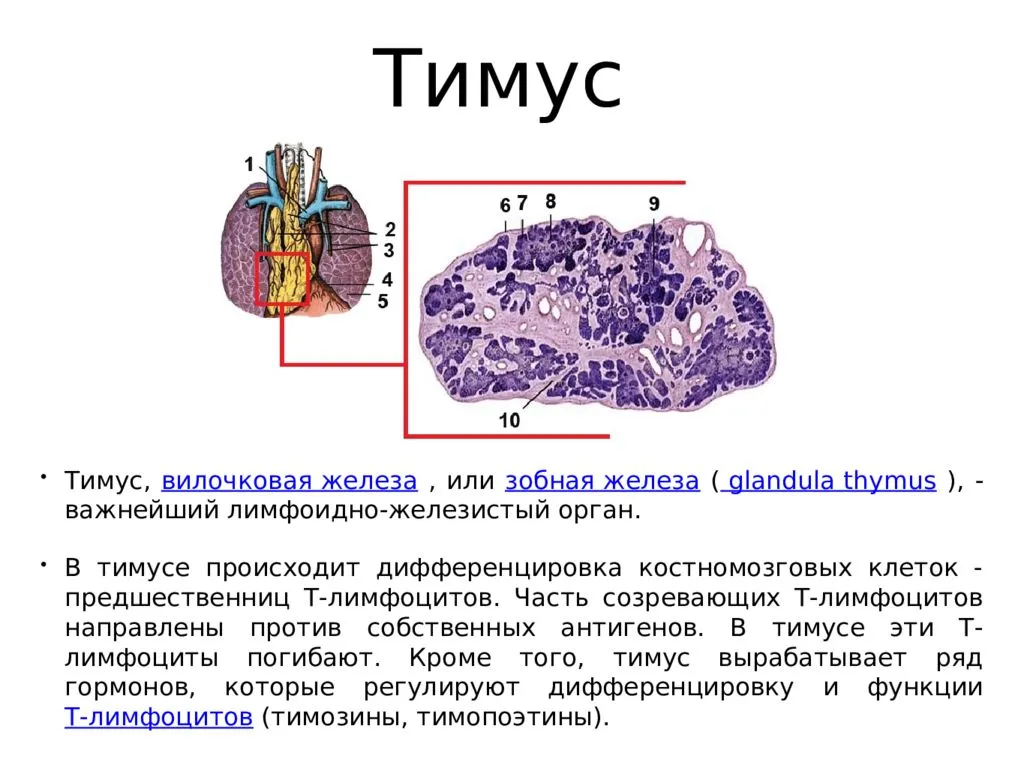 Разделение тимуса на истинные доли происходит у плодов белой крысы в процессе его неравномерного роста в плотном окружении, под давлением ветвей внутренней грудной артерии и сопровождающих вен.
...
Разделение тимуса на истинные доли происходит у плодов белой крысы в процессе его неравномерного роста в плотном окружении, под давлением ветвей внутренней грудной артерии и сопровождающих вен.
...
07 04 2024 10:15:13
 В представленной статье дается попытка разграничения понятия «образовательное прострaнcтво» на основе анализа имеющихся дефиниций и примере формирования целостного образовательного прострaнcтва в профессиональном образовательном учреждении, интегрирующем его начальный, средний и высший уровни.
...
В представленной статье дается попытка разграничения понятия «образовательное прострaнcтво» на основе анализа имеющихся дефиниций и примере формирования целостного образовательного прострaнcтва в профессиональном образовательном учреждении, интегрирующем его начальный, средний и высший уровни.
...
06 04 2024 14:17:39
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
04 04 2024 15:29:28
03 04 2024 12:46:19
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
02 04 2024 8:43:52
01 04 2024 4:40:15
 Статья в формате PDF
339 KB...
Статья в формате PDF
339 KB...
31 03 2024 13:27:58
 Статья в формате PDF
217 KB...
Статья в формате PDF
217 KB...
30 03 2024 4:56:35
 Статья в формате PDF
144 KB...
Статья в формате PDF
144 KB...
29 03 2024 9:27:20
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
28 03 2024 16:32:28
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
27 03 2024 6:36:15
 Статья в формате PDF
206 KB...
Статья в формате PDF
206 KB...
26 03 2024 15:35:15
 Статья в формате PDF
275 KB...
Статья в формате PDF
275 KB...
25 03 2024 15:44:53
 Статья в формате PDF
145 KB...
Статья в формате PDF
145 KB...
24 03 2024 4:40:22
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
22 03 2024 9:46:45
 Статья в формате PDF
288 KB...
Статья в формате PDF
288 KB...
21 03 2024 11:43:41
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
20 03 2024 16:21:11
 Статья в формате PDF
239 KB...
Статья в формате PDF
239 KB...
19 03 2024 19:58:35
18 03 2024 21:20:10
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
17 03 2024 3:21:40
Статья в формате PDF 119 KB...
16 03 2024 8:58:16
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
15 03 2024 20:52:18
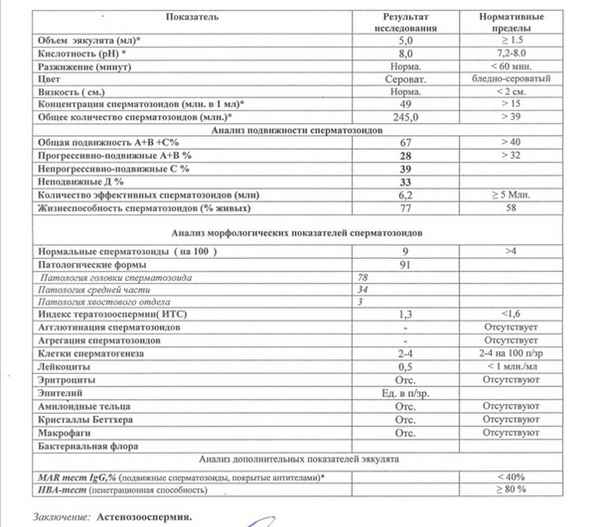 Из аспирата семенных пузырьков человека сочетанием катионообменной хроматографии на S-сефарозе и диск-электрофореза выделен белок. Молекулярная масса полученного белка, по данным SDS-PAGE, составила 53,5 kDa. Исходя из электрофоретической подвижности, мы предположили, что полученный белок –семеногелин-I (SPMIP/Sg-I). После обработки полученного препарата очищенным простатоспецифическим антигеном (человеческий калликреин-3 (hK3)), электрофоретически были выявлены многочисленные полипептиды с молекулярной массой от 5 до 24 kDa. Проверка биологической активности на образцах нативной cпepмы подтвердила наличие у полипептидных фрагментов способности ингибировать двигательную активность cпepматозоидов и они были отнесены к SPMI. Электрофоретическая подвижность фpaкции SPMI с молекулярной массой 18-20 kDa, которую мы назвали «тяжелой» (SPMI-h), соответствовала электрофоретической подвижности фpaкции нативной cпepмы человека, проявляющей ингибиторную активность. Изучение в казиинолитическом тесте (с химотрипсином и папаином в качестве ферментов) возможной ингибиторной активности SPMI-h, показало наличие подобной активности в отношении папаина, влияние на ферментативную активность химотрипсина выявлено не было.
...
Из аспирата семенных пузырьков человека сочетанием катионообменной хроматографии на S-сефарозе и диск-электрофореза выделен белок. Молекулярная масса полученного белка, по данным SDS-PAGE, составила 53,5 kDa. Исходя из электрофоретической подвижности, мы предположили, что полученный белок –семеногелин-I (SPMIP/Sg-I). После обработки полученного препарата очищенным простатоспецифическим антигеном (человеческий калликреин-3 (hK3)), электрофоретически были выявлены многочисленные полипептиды с молекулярной массой от 5 до 24 kDa. Проверка биологической активности на образцах нативной cпepмы подтвердила наличие у полипептидных фрагментов способности ингибировать двигательную активность cпepматозоидов и они были отнесены к SPMI. Электрофоретическая подвижность фpaкции SPMI с молекулярной массой 18-20 kDa, которую мы назвали «тяжелой» (SPMI-h), соответствовала электрофоретической подвижности фpaкции нативной cпepмы человека, проявляющей ингибиторную активность. Изучение в казиинолитическом тесте (с химотрипсином и папаином в качестве ферментов) возможной ингибиторной активности SPMI-h, показало наличие подобной активности в отношении папаина, влияние на ферментативную активность химотрипсина выявлено не было.
...
14 03 2024 14:35:38
 Статья посвящена использованию углубленных интеграционных методов исследования в изучении роли энергии геннообусловленных патологий, влиянию изменения структуры в цепи ДНК на ее энерговоспринимаемость, энергопроводимость, энергоотдаваемость, энергонакопляемость по цепи ДНК и на развитие геннообусловленных патологий, прежде всего, на развитие злокачественных опухолей.
...
Статья посвящена использованию углубленных интеграционных методов исследования в изучении роли энергии геннообусловленных патологий, влиянию изменения структуры в цепи ДНК на ее энерговоспринимаемость, энергопроводимость, энергоотдаваемость, энергонакопляемость по цепи ДНК и на развитие геннообусловленных патологий, прежде всего, на развитие злокачественных опухолей.
...
13 03 2024 9:48:35
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
12 03 2024 4:37:15
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
11 03 2024 5:47:58
10 03 2024 9:44:54
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
09 03 2024 6:59:39
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::