О ДЛИННОВОЛНОВЫХ МОДЕЛЯХ УДАРНЫХ ПАР
1. Ниже, строится очередная (ср.[1]) уточняющая модель фундаментального понятия классической физики и механики - ударной пары, рассматриваемой в длинноволновом приближении. Откажемся от предположения о локализации удара в точке и рассмотрим натянутую нить (струну), вибрирующую вблизи неподвижной твердой стенки. Ограничение хода может также быть и двухсторонним. Системы такого типа обычно называют системами с распределенными ударными элементами.
2. Уравнения движения в простейшем случае имеют вид:
где u(x,t) - прогиб струны, c - скорость звука, b(...) -функция диссипации; индексация по независимым переменным обозначает дифференцирование; Р(х,t) - распределение внешней силы; Ф(u, ut) - динамическая хаpaктеристика удара. В уравнении (1) операторная функция b могут иметь весьма сложную структуру, определяемую действующими гипотезами о диссипации. К уравнения (1) добавляются граничные условия.
Система (1) может быть также записана при помощи операторов динамической податливости. В случае простейших линейных моделей трения структура соответствующих операторных уравнений следующая [2]:
где операторы L (y;p) определены, например, в [2]; p -оператор дифференцирования по времени t; X - область изменения прострaнcтвенной координаты. Например, X=[l1,l2], где l1,2.- координаты концов струны.
3. Аналитическое исследование задачи может быть проведено методами частотно-временного анализа [2]. В случае Т- периодического внешнего возбуждения, для отыскания T-периодических, а также, например, субгармонических или комбинационных (l:q) режимов движения строится двухфункциональное представление, следующее из (2):
где J(x)≥0 и φ(х) - распределения импульса и фазы взаимодействия в ударном элементе; tj - соответствующий момент взаимодействия; 0<φ(х) ≤Т; х € X . Для их нахождения необходимо привлечь дополнительные соотношения, следующие из принятых гипотез ударного взаимодействия.
Полученные решения должны быть проанализированы на устойчивость и выполнимость ряда очевидных геометрических условий [1, 2].
4. Существенные динамические эффекты. Далее мы кратко обсудим некоторые существенные эффекты, найденные при анализе модели (1). Внешнее возбуждение было выбрано синусоидальным.
Главный результат - нахождение периодических режимов с синхронными взаимодействиями в отдаленных точках системы (ср [1]). Такие режимы и в данном случае распределенных ударных элементов названы «хлопками».
Как и в дискретных коротковолновых моделях, реализации хлопков система ведет себя традиционно: имеют место эффекты затягивания по частоте и амплитуде, жесткого запуска и другие, хаpaктерные для классических ударных осцилляторов.
Многие свойства хлопков оказываются подобными свойствам собственных форм линейных колебаний струны. Так, например, легко построить «высшие» формы хлопков. Такие формы особенно просто строятся для случаев двусторонних ограничителей.
Вместе с тем были также обнаружены и описаны стоячие волны с более сложными профилями (так называемые набегающие волны и др.).
Наряду с указанными частотно-временными аналитическими методами были использованы, естественно, и численные метода анализа. Их применение особенно актуально при усложнении моделей. Однако, в силу того, что частотно - временные методы позволяют привести уравнения движения к виду без сингулярных обобщенных функции, лучший результат дают комбинированные методы, так как в отсутствии разрывов эффективность всех численных процедур существенно возрастает.
Указанные эффекты нашли экспериментальное обоснование на стендах, разработанных А.М. Веприком при участии автора в ИМАШ РАН.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты 09-01-00720-а).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Крупенин В. Л. О коротковолновых моделях ударных пар// Фундаментальные исследования. - 2008, №3. -С.86-88.
- Babitsky V.I.,. Krupenin V.L. Vibration of Strongly Nonlinear Discontinuous Systems.- Berlin. Heidelberg, New York: Springer-Verlag, 2001. -404 p.p.
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
19 04 2024 1:48:17
 Статья в формате PDF
264 KB...
Статья в формате PDF
264 KB...
18 04 2024 12:13:14
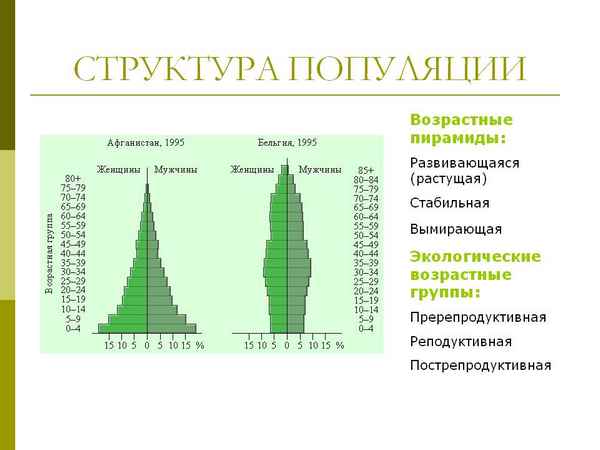 Изучены онтогенез и возрастная структура ценопопуляций многолетних травянистых поликарпических видов, относящихся к различным типам экобиоморф: стержнекорневых – дягиль лекарственный (Angenica archangelica L.) и цикорий обыкновенный (Cichorium intybus L.) и длиннокорневищных – вязель разноцветный (Coronilla varia L.).В онтогенезе выбранных видов выделены следующие 4 периода и 9 возрастных состояний: 1). период первичного покоя (покоящиеся семена); 2). виргинильный период (проростки, ювенильное, имматурное, виргинильное); 3). генеративный (молодое, средневозрастное, старое генеративное); 4). сенильный (сенильное).
Изучение возрастной структуры ценопопуляций данных видов было проведено в сравнительно-георафическом аспекте с учетом приуроченности к определенным типам растительных сообществ. Установлено наличие полночлeнных возрастных спектров, представленых прегенеративными, генеративными и сенильными растениями с преобладанием молодых вегетирующих особей. Преобладающим типом самоподдержания дягиля и цикория является семенное, а вязеля – вегетативное размножение.
Отмечено, что возрастные спектры ценопопуляций выбранных видов имеют адаптивный хаpaктер, заметно меняются в зависимости от условий внешней среды и антропогенного воздействия и отражают флуктуационный хаpaктер динамических процессов в фитоценозах.
...
Изучены онтогенез и возрастная структура ценопопуляций многолетних травянистых поликарпических видов, относящихся к различным типам экобиоморф: стержнекорневых – дягиль лекарственный (Angenica archangelica L.) и цикорий обыкновенный (Cichorium intybus L.) и длиннокорневищных – вязель разноцветный (Coronilla varia L.).В онтогенезе выбранных видов выделены следующие 4 периода и 9 возрастных состояний: 1). период первичного покоя (покоящиеся семена); 2). виргинильный период (проростки, ювенильное, имматурное, виргинильное); 3). генеративный (молодое, средневозрастное, старое генеративное); 4). сенильный (сенильное).
Изучение возрастной структуры ценопопуляций данных видов было проведено в сравнительно-георафическом аспекте с учетом приуроченности к определенным типам растительных сообществ. Установлено наличие полночлeнных возрастных спектров, представленых прегенеративными, генеративными и сенильными растениями с преобладанием молодых вегетирующих особей. Преобладающим типом самоподдержания дягиля и цикория является семенное, а вязеля – вегетативное размножение.
Отмечено, что возрастные спектры ценопопуляций выбранных видов имеют адаптивный хаpaктер, заметно меняются в зависимости от условий внешней среды и антропогенного воздействия и отражают флуктуационный хаpaктер динамических процессов в фитоценозах.
...
17 04 2024 17:33:25
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
15 04 2024 14:14:45
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
14 04 2024 0:23:35
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
13 04 2024 3:58:41
 Статья в формате PDF
251 KB...
Статья в формате PDF
251 KB...
11 04 2024 14:32:20
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
10 04 2024 0:13:19
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
09 04 2024 2:13:44
 Статья в формате PDF
303 KB...
Статья в формате PDF
303 KB...
05 04 2024 10:26:47
04 04 2024 10:19:18
 Статья в формате PDF
131 KB...
Статья в формате PDF
131 KB...
03 04 2024 6:40:24
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
01 04 2024 23:33:40
31 03 2024 19:33:25
Статья в формате PDF 120 KB...
30 03 2024 15:51:33
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
29 03 2024 13:25:52
 Статья в формате PDF
322 KB...
Статья в формате PDF
322 KB...
27 03 2024 2:19:52
 Статья в формате PDF
304 KB...
Статья в формате PDF
304 KB...
26 03 2024 3:19:24
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
25 03 2024 8:43:53
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
24 03 2024 5:12:23
23 03 2024 5:28:33
 Статья в формате PDF
173 KB...
Статья в формате PDF
173 KB...
22 03 2024 17:52:33
 Статья в формате PDF
344 KB...
Статья в формате PDF
344 KB...
21 03 2024 20:39:56
 Понятие время является важнейшим понятием, как физики, так и философии. Актуальность этой проблемы обусловлена тем, что до сих пор, несмотря на широкий круг исследований, не сложилось твердо закрепленного представления о времени. В статье делается попытка раскрыть сущность понятия времени и связать меру времени с движением. За меру времени механического движения предлагается выбрать путь, пройденный, например, концом стрелки часов, участвующей не только в собственном движении относительно циферблата, как это принято, но и в сложном движении, включающем движение часов как целое относительно внешнего наблюдателя. Синхронизация хода часов производится по периодам их движений в соответствие с принятым эталоном времени. Рассматривается случай, когда часы движутся относительно внешнего наблюдателя с постоянной скоростью. Такой подход к проблеме времени позволяет понять его непрерывность и бесконечность.
...
Понятие время является важнейшим понятием, как физики, так и философии. Актуальность этой проблемы обусловлена тем, что до сих пор, несмотря на широкий круг исследований, не сложилось твердо закрепленного представления о времени. В статье делается попытка раскрыть сущность понятия времени и связать меру времени с движением. За меру времени механического движения предлагается выбрать путь, пройденный, например, концом стрелки часов, участвующей не только в собственном движении относительно циферблата, как это принято, но и в сложном движении, включающем движение часов как целое относительно внешнего наблюдателя. Синхронизация хода часов производится по периодам их движений в соответствие с принятым эталоном времени. Рассматривается случай, когда часы движутся относительно внешнего наблюдателя с постоянной скоростью. Такой подход к проблеме времени позволяет понять его непрерывность и бесконечность.
...
20 03 2024 22:23:33
 Статья в формате PDF
254 KB...
Статья в формате PDF
254 KB...
19 03 2024 18:40:43
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
18 03 2024 17:36:13
 Статья в формате PDF
637 KB...
Статья в формате PDF
637 KB...
17 03 2024 17:25:29
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
16 03 2024 22:33:53
 Статья в формате PDF
284 KB...
Статья в формате PDF
284 KB...
15 03 2024 4:48:22
 Статья в формате PDF
315 KB...
Статья в формате PDF
315 KB...
14 03 2024 18:20:20
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
13 03 2024 10:54:35
 В статье рассматривается взаимодействие тел при различных скоростях и делается вывод о несправедливости постулата о постоянстве скорости света относительно любой системы отсчета. Дается также понятное с точки зрения классической механики объяснение зависимости длины и времени от скорости.
...
В статье рассматривается взаимодействие тел при различных скоростях и делается вывод о несправедливости постулата о постоянстве скорости света относительно любой системы отсчета. Дается также понятное с точки зрения классической механики объяснение зависимости длины и времени от скорости.
...
12 03 2024 8:41:14
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
11 03 2024 13:19:44
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::