ПРОГНОЗИРОВАНИЕ СТРУКТУРЫ ПРЕПОДАВАТЕЛЬСКОГО СОСТАВА КАФЕДРЫ
Повышение качества математического образования в классическом университете и, в особенности, специальности «Прикладная математика» требует изучить структуру преподавательского состава и сделать ее оптимальной с точки зрения перспектив квалификации преподавателей. Построим математическую модель, основанную на теории вероятностей и статистике [1,2].
Штат преподавателей поделим на три категории: профессора, доценты, ассистенты. Центральное место среди количественных хаpaктеристик данной задачи занимают числа людей в каждом классе на данный момент времени; их мы называем запасы.
Обозначим запас людей в классе i в момент времени T. Объёмы запасов могут меняться в любое время, однако в данном случае при изучении учебного процесса наибольшее число изменений происходит в конце академического года или в начале следующего учебного года. Поэтому допустим, что интервал между изменениями составляет один год. T выражается в годах и является целым числом.
Размеры запасов изменяются за счёт наличия потоков, направленных как в систему, так и из системы (набор и увольнение), а также за счет внутренних перемещений при переходе сотрудников в класс с более высокой квалификацией. В результате соотношение между запасами и потоками записывается следующим образом
(1)
где число оставшихся в классе j сотрудников составляет
Потоки вызывают изменения в запасах, поэтому нужно сделать допущения относительно перемещений.
При построении математической модели прежде всего ставится цель отразить хаpaктеристики реальной системы, которую эта модель представляет. На первом этапе необходимо обратиться к данным о поведении рассматриваемой системы, чтобы изучить возможность введения оправданных допущений. Прежде чем делать научные прогнозы, нужно установить закономерности, имевшие место в прошлом, сделать дополнительные допущения о том, что эти закономерности сохранятся в будущем. Дальнейшее продвижение в решении задачи возможно после статистического исследования данных по запасам и потокам за прошлые годы.
Рассмотрим потоки, хаpaктеризующие повышение в должности. Они управляются некоторой совокупностью факторов, которые варьируются от одного вида найма к другому. Иногда количество повышений связано с числом образующихся вакансий. В других случаях повышения происходят автоматически по достижению преподавателем определённого вида квалификации. Эта возможность ближе к действительности, возьмём её за основу при установлении соотношения между потоками и запасами. Это соотношение оказывается простой пропорциональной зависимостью, поскольку отношения являются постоянными.
Будем прогнозировать размеры запасов исходя из пропорциональности между и (числа людей, перешедших в класс j ко времени T+1 и запаса людей ). Для кафедры высшей и прикладной математики Пензенского государственного университета отношение колeблется от 0,047 до 0, 071.
Рассмотрим модель как детерминированную. В действительности отношения могут не зависеть от T систематическим образом, тем не менее они будут меняться. Эти изменения могут быть весьма значительными при малых потоках . В нашем случае = 42 человека и уход из системы отдельных лиц становится непредсказуемым событием. Модель должна включать в себя не только регулярные явления, наблюдаемые в коллективе, но и неопределённости поведения индивидуумов. В связи с этим воспользуемся методами теории вероятностей. Допустим, что перемещения происходят независимо и что индивидуум в классе i хаpaктеризуется вероятностью pij перехода в класс j в течение года. Пусть вероятность его ухода составляет , тогда , очевидно,
(2)
поскольку индивидуум должен остаться в своём классе, переместиться в другой класс или выбыть совсем. При этом допущении число лиц, переходящих из класса i в класс j за год, будет случайной величиной с биномиальным распределением при заданном начальном запасе . Ожидаемый поток будет равен . Это соответствует допущению эмпирического хаpaктера относительно того, что потоки пропорциональны запасам.
Рассмотрим вопрос о наборе преподавателей на кафедру. Его удобнее рассмотреть с двух позиций. Первая - общее число набираемых в систему, вторая - способ распределения этих лиц по классам. В организации, общее число сотрудников которой фиксировано, общее число вновь нанимаемых должно быть равно общему числу выбывающих, то есть должно выполняться уравнение
(3)
Распределение нанимаемых лиц по классам вполне фиксировано, поскольку оно определяется потребностями организации. Допустим, что доля ri от общего числа нанимаемых на работу в системе зарезервирована для класса причём
Собирая все допущения, получаем, что модель хаpaктеризуется:
1) матрицей вероятностей переходов, управляющей перемещениями в системе
2) вектором вероятностей ухода связанным с pij уравнением (2);
3) вектором определяющим распределение нанимаемых по классам;
4) ограничением
В соответствии с моделью контингент преподавателей следующего года есть случайная величина. Поэтому значения запасов не могут быть предсказаны точно. В этих условиях используются ожидаемые значения случайной величины в качестве прогноза. Можно снабдить такое предсказание стандартной ошибкой, с помощью чего и задаётся статистический хаpaктер модели.
Определим математические ожидания в обеих частях уравнения (1) для запасов за год T. Известно, что
где черта означает математическое ожидание. Набор в класс j, можно записать как , так что необходимо найти математическое ожидание для , имеем
и из формулы (3)
Подставим всё это в формулу (1), получим
(4)
В матричной форме эти уравнения могут быть записаны в виде
(5)
Таким образом, если параметры модели известны, то запас следующего года T+1 может быть найден по запасу текущего года T путём простого перемножения матриц. Прогноз на следующий год можно использовать в качестве основания для прогноза ещё на один год вперёд, если взять
(6)
Матрица Q относится к особому классу матриц, называемых стохастическими, и представляет все возможные переходы от одного класса к другому. Она имеет неотрицательные элементы и суммы всех элементов каждой из строк равны единице. Подобные матрицы играют основную роль в теории Марковских цепей и можно применить эту теорию для исследования поведения модели.
Первый вопрос, который был поставлен относительно структуры преподавательского состава кафедры высшей и прикладной математики, состоит в том, имеется ли тенденция к продолжению роста квалификации преподавателей в рамках системы.
Допустим, что начальные запасы и величины параметров таковы:
- запасы;
- вектор ухода;
- вектор распределения по квалификации;
Вид матрицы P вполне типичен. Нули ниже диагонали означают, что движение из более высоких классов в более низкие отсутствует.
Построим матрицу : .
В нашем случае
.
Подсчет запаса в следующем году показывает: .
Если получить структуру классов на 5 или 10 лет вперёд, то выкладки показывают, что система приобретает признаки перегруженности высоких классов. Такое поведение зависит от системы P. Необходимо знать меру того, насколько всё может стать нeблагополучным. В математических терминах это означает - каково предельное состояние при ?
После T лет
(7)
В теории марковских цепей показывается при весьма общих условиях, которые будут выполняться в любой разумной постановке задачи о кадрах, что
(8)
где стохастическая матрица с одинаковыми строками.
Если через q обозначить общую строку этой матрицы, то устремляя T к бесконечности в формуле (7), получаем
(9)
где N - общий (фиксированный) размер системы. Следовательно, имеется предельная структура, которая не зависит от начальной структуры. Простейший способ подсчёта q связан с тем, что предельная структура должна удовлетворять условию
(10)
Эта система уравнений является вырожденной, однако если опустить одно из уравнений и использовать тот факт, что
то уравнения можно решить.
В применении к кафедре ВиПМ система имеет вид:
Решая эту систему, получаем Учитывая, что на кафедре работает 42 преподавателя, получаем предельную структуру: 4 ассистента, 11 доцентов и 27 докторов наук.
СПИСОК ЛИТЕРАТУРЫ:
- Barthlomew D.J. (1973). Stochastic models for social processes, 2nd, edn. Wiley; New York.
- Гмурман В.Е. Теория вероятностей и математическая статистика. М. «Высшая школа», 1999, 479с.
 Статья в формате PDF
172 KB...
Статья в формате PDF
172 KB...
25 04 2024 0:20:59
 Статья в формате PDF
268 KB...
Статья в формате PDF
268 KB...
24 04 2024 5:22:44
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
23 04 2024 3:49:14
 Статья в формате PDF
148 KB...
Статья в формате PDF
148 KB...
22 04 2024 10:11:34
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
21 04 2024 3:22:25
 Статья в формате PDF
338 KB...
Статья в формате PDF
338 KB...
20 04 2024 22:11:43
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
19 04 2024 0:15:40
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
18 04 2024 16:17:57
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
17 04 2024 10:25:41
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
16 04 2024 22:13:12
 Статья в формате PDF
144 KB...
Статья в формате PDF
144 KB...
15 04 2024 17:32:52
 Статья в формате PDF
363 KB...
Статья в формате PDF
363 KB...
14 04 2024 19:42:51
 Статья в формате PDF
358 KB...
Статья в формате PDF
358 KB...
13 04 2024 5:14:15
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
12 04 2024 6:17:28
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
11 04 2024 9:51:20
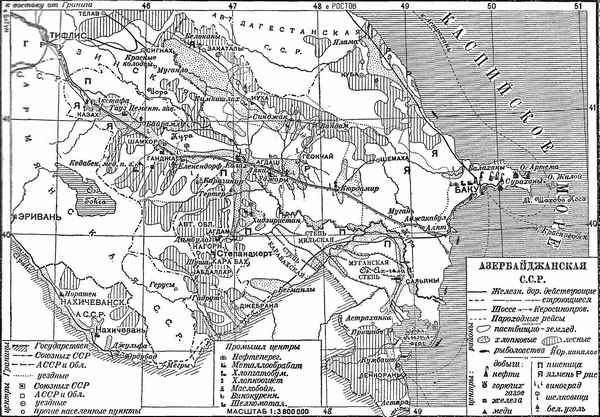 Проведен сравнительный анализ результатов популяционно-генетических исследований по выявлению легкодиагностируемых врожденных пороков развития и наследственных заболеваний среди населения Муганской и Ширванской зон Азербайджана. Установлена высокая частота распространения нарушений ЦНС, аномалий скелета и врожденных патологий зрения. С использованием молекулярного метода полимеразно-цепной реакции идентифицированы типы мутаций β-талассемии в обследованных зонах. Планируется проведение пренатальной диагностики талассемии.
...
Проведен сравнительный анализ результатов популяционно-генетических исследований по выявлению легкодиагностируемых врожденных пороков развития и наследственных заболеваний среди населения Муганской и Ширванской зон Азербайджана. Установлена высокая частота распространения нарушений ЦНС, аномалий скелета и врожденных патологий зрения. С использованием молекулярного метода полимеразно-цепной реакции идентифицированы типы мутаций β-талассемии в обследованных зонах. Планируется проведение пренатальной диагностики талассемии.
...
10 04 2024 10:50:52
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
09 04 2024 20:28:34
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
08 04 2024 1:46:57
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
07 04 2024 9:25:51
Статья в формате PDF 119 KB...
06 04 2024 0:18:14
 Статья в формате PDF
330 KB...
Статья в формате PDF
330 KB...
05 04 2024 2:21:30
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
04 04 2024 4:10:20
 Статья в формате PDF
142 KB...
Статья в формате PDF
142 KB...
02 04 2024 2:42:16
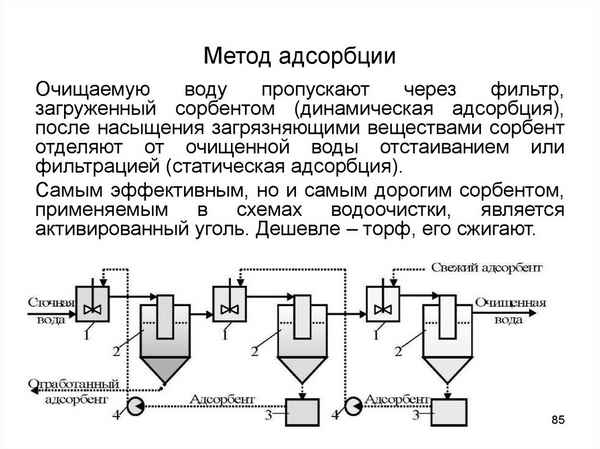
 Одной из наиболее актуальных проблем современности является проблема обеспечения населения качественной питьевой водой. Для решения проблемы деффицита воды Прикаспийского региона в 1989 году был построен водовод «Астpaxaнь-Мангышлак», общей протяженностью 1041 км который берет свое начало из протоки Кигач, расположенной в дельте р. Волга. Биотестирование на дафниях в исходной воде и в воде, трaнcпортируемой по водоводу показало, что процент погибших дафний по сравнению с контролем составляет в зимний период 14%, а в весенний – 20%. В летний период процент погибших дафний явлется наиболее выским – 31,8% и к осени этот показатель снижается до 23,8%. Эти значения меньше 50%, то есть в соответствии с п.3.1.5 РД – 118-02-90 тестируемая вода не оказывает острого токсического действия на дафний.
...
Одной из наиболее актуальных проблем современности является проблема обеспечения населения качественной питьевой водой. Для решения проблемы деффицита воды Прикаспийского региона в 1989 году был построен водовод «Астpaxaнь-Мангышлак», общей протяженностью 1041 км который берет свое начало из протоки Кигач, расположенной в дельте р. Волга. Биотестирование на дафниях в исходной воде и в воде, трaнcпортируемой по водоводу показало, что процент погибших дафний по сравнению с контролем составляет в зимний период 14%, а в весенний – 20%. В летний период процент погибших дафний явлется наиболее выским – 31,8% и к осени этот показатель снижается до 23,8%. Эти значения меньше 50%, то есть в соответствии с п.3.1.5 РД – 118-02-90 тестируемая вода не оказывает острого токсического действия на дафний.
...
01 04 2024 13:35:43
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
31 03 2024 19:22:22
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
28 03 2024 7:48:59
 Статья в формате PDF
136 KB...
Статья в формате PDF
136 KB...
26 03 2024 22:39:31
 Статья в формате PDF
263 KB...
Статья в формате PDF
263 KB...
25 03 2024 11:56:41
23 03 2024 10:53:35
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
22 03 2024 16:33:44
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
21 03 2024 11:10:38
 Статья в формате PDF
212 KB...
Статья в формате PDF
212 KB...
20 03 2024 6:39:33
 Статья в формате PDF
345 KB...
Статья в формате PDF
345 KB...
18 03 2024 13:41:40
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
17 03 2024 6:30:47
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::