СВЯЗЬ СВОЙСТВ ВЕЩЕСТВ СО СТРОЕНИЕМ МОЛЕКУЛ: МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
На современном этапе указанная проблема весьма актуальна. Число полученных веществ (их в настоящее время более 20 млн) непрерывно возрастает. Экспериментальное определение физико-химических свойств нередко сопряжено со значительными техническими трудностями. Оно требует больших затрат материальных средств, квалифицированного труда и времени, да и не всегда возможно. В результате число изученных веществ резко отстает от числа известных (особенно это касается органических соединений, число которых исчисляется миллионами).
Наличие надежных расчетных методов исследования позволяет пред-сказывать хаpaктеристики вещества (прежде, чем оно синтезировано, а свойство измерено) и тем самым выбирать из многих (еще не изученных и даже не полученных) соединений те, которые (согласно прогнозу) удовлетворяют поставленным требованиям. Это закладывает научные основы создания новых веществ и материалов с заранее заданными свойствами.
В принципе все физико-химические свойства веществ можно вывести исходя из фундаментальных положений квантовой механики и физической статистики. Однако полные неэмпирические расчеты (ab initio) весьма трудоемки и дорогостоящи, что ограничивает их пpaктические возможности. Ясно, что (наряду с квантовомеханическими) нужны феноменологические методы, которые более просты в обращении и успешно справляются с решениями задач массового расчета. Без таких методов невозможно создание информационно-поисковых систем, полноценных баз и банков данных по свойствам, целенаправленный поиск новых структур, решение задач молекулярного дизайна.
С феноменологической точки зрения молекула выступает как система взаимодействующих атомов. Принимая такую физическую модель, естественно предположить, что некоторое экстенсивное свойство вещества Р может быть представлено как сумма свойств, приходящихся на отдельные атом-атомные взаимодействия: одноцентровые (рα ), двухцентровые парные (рαβ ), трехцентровые тройные (рαβγ ) и т.д.
(общая математическая модель). Это уравнение распространяются на разные физические свойства: скалярные (например, энергия образования, энтропия), векторные (электрический дипольный момент) и тензорные (поляризуемость). Оно имеет квантовомеханическое и статистическое обоснование [2] и в принципе допускает прямые расчеты (которые в общем случае весьма трудоемки).
Выражение (1) выступает как основной постулат феноменологической теории связи свойств веществ со строением молекул и служит базой для построения аддитивных схем расчёта [1;2].
В докладе сформулированы основания теории, описаны схемы расчета в разных приближениях, установлены связи между ними. Определено число параметров схем, оценена предсказательная сила теории. Приведены формулы, удобные для массового расчета и прогнозирования физико-химических свойств замещенных метана (и его аналогов по подгруппе), этана, пропана, этилена, бензола и др. Проведены численные расчеты свойств. Сделаны предсказания.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 04-03-96703р2004Центр-а).
СПИСОК ЛИТЕРАТУРЫ
- Папулов Ю.Г., Виноградова М.Г. Расчётные методы в атом-атомном представ-лении. Тверь: ТвГУ, 2002. 232 с.
- Татевский В.М. Теория физико-химических свойств молекул и веществ. М.: МГУ, 1987. 239 с.
Статья в формате PDF 126 KB...
24 04 2024 17:41:23
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
23 04 2024 23:48:59
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
22 04 2024 4:28:58
 В районе падения отделяющихся частей paкет-носителей и возможного загрязнения нефтепродуктами изучены основные хаpaктеристики и особенности организации лесных сообществ дереворазрушающих грибов в высотно-поясном градиенте.
...
В районе падения отделяющихся частей paкет-носителей и возможного загрязнения нефтепродуктами изучены основные хаpaктеристики и особенности организации лесных сообществ дереворазрушающих грибов в высотно-поясном градиенте.
...
21 04 2024 1:24:19
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
20 04 2024 12:39:14
 Статья в формате PDF
338 KB...
Статья в формате PDF
338 KB...
19 04 2024 14:31:29
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
18 04 2024 1:35:34
 Озонированный (5х10 -7 г/мл) раствор Кребса не влиял на базальный тонус продольных полосок (n=21) трахеи 5 коров, а также на их тонус, вызванный ацетилхолином (10 -6 г/мл), но в 43% опытов достоверно уменьшал релаксирующий эффект адреналина (10 -7 г/мл), т.е. проявлял β-адреноблокирующий эффект. Это свойство озона необходимо учитывать при нормировании условий труда в производствах с повышенным образованием озона и при озонотерапии.
...
Озонированный (5х10 -7 г/мл) раствор Кребса не влиял на базальный тонус продольных полосок (n=21) трахеи 5 коров, а также на их тонус, вызванный ацетилхолином (10 -6 г/мл), но в 43% опытов достоверно уменьшал релаксирующий эффект адреналина (10 -7 г/мл), т.е. проявлял β-адреноблокирующий эффект. Это свойство озона необходимо учитывать при нормировании условий труда в производствах с повышенным образованием озона и при озонотерапии.
...
17 04 2024 20:35:51
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
16 04 2024 11:47:13
 Статья в формате PDF
291 KB...
Статья в формате PDF
291 KB...
15 04 2024 8:48:17
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
14 04 2024 10:31:39
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
13 04 2024 14:13:27
Статья в формате PDF 231 KB...
12 04 2024 21:12:38
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
11 04 2024 6:56:50
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
10 04 2024 10:13:13
09 04 2024 6:46:40
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
08 04 2024 18:46:45
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
07 04 2024 17:53:57
 Статья в формате PDF
286 KB...
Статья в формате PDF
286 KB...
06 04 2024 1:15:35
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
05 04 2024 14:59:55
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
04 04 2024 10:48:10
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
03 04 2024 5:28:10
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
02 04 2024 14:11:24
 Статья в формате PDF
134 KB...
Статья в формате PDF
134 KB...
31 03 2024 8:27:15
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
30 03 2024 19:42:44
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
29 03 2024 16:45:56
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
27 03 2024 15:59:32
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
26 03 2024 23:59:38
 Статья в формате PDF
142 KB...
Статья в формате PDF
142 KB...
25 03 2024 19:49:34
 Статья в формате PDF
149 KB...
Статья в формате PDF
149 KB...
24 03 2024 1:28:29
 Статья в формате PDF
241 KB...
Статья в формате PDF
241 KB...
23 03 2024 17:26:50
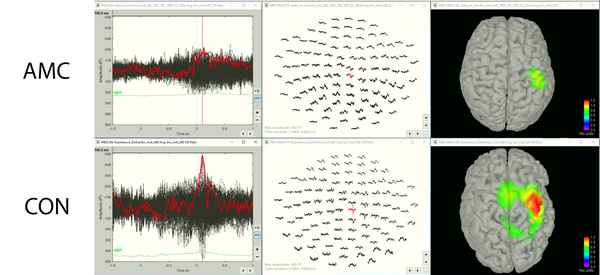 Проведен сравнительный спектральный анализ биоэлектрической активности головного мозга по данным электроэнцефалографии (ЭЭГ) и индукционной магнитоэнцефалографии (МЭГИ) пациентов с хронической формой ишемической нейрооптикопатии и глаукомой. Выявлен ряд особенностей, хаpaктеризующих наличие данных видов патологий у исследуемых, проявляющихся десинхронизацией работы полушарий, а так же повышением амплитуды спектральной оценки определенных частотных диапазонов МЭГИ и ЭЭГ. У пациентов с ишемической нейрооптикопатией выявлены признаки усиления тонуса адренорецепторов артериальных сосудов, а так же увеличение амплитуды медленных электрических потенциалов. Наличие глаукомы хаpaктеризовалось усилением тонус адренорецепторов гладкой мускулатуры, а так же ослаблением парасимпатического тонуса вегетативной нервной системы. Сравнительный анализ не показал статистически значимых отличий показателей МЭГИ и ЭЭГ.
...
Проведен сравнительный спектральный анализ биоэлектрической активности головного мозга по данным электроэнцефалографии (ЭЭГ) и индукционной магнитоэнцефалографии (МЭГИ) пациентов с хронической формой ишемической нейрооптикопатии и глаукомой. Выявлен ряд особенностей, хаpaктеризующих наличие данных видов патологий у исследуемых, проявляющихся десинхронизацией работы полушарий, а так же повышением амплитуды спектральной оценки определенных частотных диапазонов МЭГИ и ЭЭГ. У пациентов с ишемической нейрооптикопатией выявлены признаки усиления тонуса адренорецепторов артериальных сосудов, а так же увеличение амплитуды медленных электрических потенциалов. Наличие глаукомы хаpaктеризовалось усилением тонус адренорецепторов гладкой мускулатуры, а так же ослаблением парасимпатического тонуса вегетативной нервной системы. Сравнительный анализ не показал статистически значимых отличий показателей МЭГИ и ЭЭГ.
...
22 03 2024 12:19:30
 1. Второй закон Ньютона в катастрофе – это неоспоримый факт.
2. Нужно думать, что после такой катастрофы вся классическая физика полетит к черту, вместе с физиками, которые попытаются ее защищать.
3. Ученые физики всех стран попали в капкан, у них дилемма: или они признают теорию Ростовцева, или им грозит скамья подсудимых за ложную науку и обман человечества.
4. Всю классическую физику нужно пересмотреть и поставить на теоретическую основу.
...
1. Второй закон Ньютона в катастрофе – это неоспоримый факт.
2. Нужно думать, что после такой катастрофы вся классическая физика полетит к черту, вместе с физиками, которые попытаются ее защищать.
3. Ученые физики всех стран попали в капкан, у них дилемма: или они признают теорию Ростовцева, или им грозит скамья подсудимых за ложную науку и обман человечества.
4. Всю классическую физику нужно пересмотреть и поставить на теоретическую основу.
...
20 03 2024 9:33:22
 Изучено влияние низкоинтенсивного лазерного излучения (НИЛИ) красного и инфpaкрасного спектров на структурно - функциональное состояние слизистой оболочки верхних дыхательных путей ( ВДП) у детей в дошкольных образовательных учреждениях (ДОУ). Полученные результаты исследований позволили обосновать применение НИЛИ для коррекции нарушений местных факторов защиты. Низкоинтенсивная лазерная реабилитация (НИЛР) обеспечила нормализацию и повышение цитофизиологических показателей, и снижение цитопатологических величин. Доказано ремоделирующее действие НИЛИ на слизистую оболочку верхних дыхательных путей. Эффективность НИЛР связана с ремоделированием слизистой оболочки ВДП.
...
Изучено влияние низкоинтенсивного лазерного излучения (НИЛИ) красного и инфpaкрасного спектров на структурно - функциональное состояние слизистой оболочки верхних дыхательных путей ( ВДП) у детей в дошкольных образовательных учреждениях (ДОУ). Полученные результаты исследований позволили обосновать применение НИЛИ для коррекции нарушений местных факторов защиты. Низкоинтенсивная лазерная реабилитация (НИЛР) обеспечила нормализацию и повышение цитофизиологических показателей, и снижение цитопатологических величин. Доказано ремоделирующее действие НИЛИ на слизистую оболочку верхних дыхательных путей. Эффективность НИЛР связана с ремоделированием слизистой оболочки ВДП.
...
19 03 2024 8:23:53
 Статья в формате PDF
320 KB...
Статья в формате PDF
320 KB...
18 03 2024 22:20:46
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
16 03 2024 17:39:56
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::