МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ НА МИКРОУРОВНЕ

Проведение исследований в области системы высшего образования, в частности, по одному из разделов высшей математике, привело к построению математической модели, позволяющей анализировать стратегию развития образования. Остановимся на микромодели образования. В рамках этой модели анализируется процесс становления специалиста. В ней на упрощённом уровне делается попытка оценить как, за какое время и в результате каких усилий в ходе обучения и пpaктической работы студент превращается в специалиста.
Составим простейшее математическое описание процесса получения высшего образования. Эта модель не позволит получить надёжные и достоверные количественные оценки, но она даёт качественное представление о механизмах изучаемых явлений и причинно-следственных связях.
Начнём с микроописания - описания процесса получения математического образования конкретным человеком.
Сформулируем основные предположения.
Будем рассматривать «массовое» математическое высшее образование («типичный человек в типичных обстоятельствах»).
Будем считать, что существует переменная величина x, которая хаpaктеризует степень профессиональной подготовки. «Профессиональному минимуму» для определённости сопоставим значение x=1. Начиная с этого момента, молодой специалист миновал стадию ученичества и готов к самостоятельной работе.
Изменение квалификации определяется временем, затраченным обществом и самим студентом. Можно сказать, что это «среднее общественно необходимое время. Изменение квалификации со временем определяется обыкновенным дифференциальным уравнением (динамической системой)
(1)
В нём x хаpaктеризует квалификацию специалиста в процессе подготовки, а затем дальнейшей деятельности, t - временная переменная, x0 - квалификация до начала обучения в ВУЗе. Функция хаpaктеризует усилия, вкладываемые системой образования в подготовку специалиста.
Уточним вид функции . Чтобы последующие рассуждения стали более наглядными, сформулируем сначала неприемлемую и заведомо неправильную модель.
1. Модель «наполняемого сосуда». Представим себе сосуд, который наполняют жидкостью до некоторой отметки . Если считать, что подготовка в высшей школе сродни равномерному наливанию жидкости в сосуд, то в уравнении (1)
при иначе (2)
где T - время обучения. При этом критическая отметка должна достигаться к концу обучения.
Главный недостаток этой модели - неспособность описать такое явление, как «инфляция вузовского диплома», противоречие между большим количеством закончивших ВУЗ по многим специальностям и очень небольшим числом квалифицированных специалистов в тех же областях.
2. Модель «зажигания огня».
Вернёмся к функции . Поставим простейший эксперимент. Пусть некий студент, прослушав первые полгода, например, курс аналитической геометрии, бросает учиться. Допустим, что с определенным временным интервалом, мы контролируем его знания. Что будет происходить? Здравый смысл подсказывает, что выученное пpaктически не применялось и не приведено в систему. Оно будет забываться. Скорость забывания зависит от способностей и индивидуальных склонностей студента.
Математическая психология и ее наиболее развитый раздел - теория обучения, утверждают, что объём знаний в этом случае будет уменьшаться по экспоненциальному закону. Классические эксперименты Г.Эбингауза показывают, что в простейшем случае объём запоминаемого материала x при будет зависеть от времени обучения следующим образом
(3)
где C1 и C2 - постоянные, α - показатель, определяющий скорость восприятия .
Исходя из этой теории, естественно считать, что на начальном этапе обучения , функция - линейная:
при (4)
Коэффициент показывает насколько легко студент в начале обучения осваивает новый материал. Чем меньше значение по абсолютной величине, тем лучше восприятие.
Посмотрим, что происходило бы, если бы вся зависимость была линейной и определялась формулой (4), а усилия системы образования вкладывались бы с постоянной интенсивностью I0. В этом случае уравнение (1), определяющее изменение уровня подготовки, запишется в виде
(5)
Решение этого уравнения таково:
(6)
Другими словами, вначале происходит довольно быстрое накопление знаний. При
(7)
Формула (7) выражает очевидный факт: чем лучше начальная подготовка (больше x0), тем лучше восприятие (больше коэффициент ), и чем интенсивнее ведется обучение (больше величина I0), тем быстрее растёт уровень подготовки.
При
(8)
Из равенства (8) следует, что в упрощённой модели (5) имеет место эффект «насыщения». То есть, существует некий предельный уровень квалификации, определяемый интенсивностью обучения I0 и восприимчивостью , выше которого студент не поднимется, сколько бы его не учили. Поскольку это не соответствует имеющимся данным и противоречит существованию самого феномена высшего образования, следует перейти к более сложной нелинейной модели.
Будем предполагать, что получение образования и подготовка специалистов требует конечных затрат общественно необходимого времени. Естественно исходить из того, что после освоения логики профессии, фундаментальных курсов, овладения понятийным аппаратом дальнейшее получение образования облегчается. Геометрически это означает, что далее кривая поворачивает вверх и пересекает ось абсцисс в точке x=1. При x<1 общество вкладывает усилия в подготовку специалиста, а при x>1 специалист начинает вкладывать усилия в повышение благосостояния общества. Иначе говоря, площадь под кривой конечна. Пусть она равна I1
(9)
Студент в рамках предложенной модели, хаpaктеризуется двумя параметрами - величиной, отражающей его способность усваивать материал на начальной стадии обучения и общим объёмом усилий, который нужно вложить, чтобы подготовить из него полноценного специалиста.
Можно рассмотреть несколько типичных ситуаций.
1). Кривую в интервале для способного студента, легко осваивающего выбранную профессию. Для него имеет малое значение.
2). Плохо воспринимающий студент, с которым нужно много возиться. Нужно предположить, что существует значительная корреляция между величинами и I1
Переход к технологической цивилизации позволил предположить такие методы и алгоритмы обучения, при которых для среднего студента , где
Во времена средневековья поэтому было возможно только простейшее профессиональное или, напротив, элитарное образование. Во время научно - технической революции величина резко увеличивается. Информационная лавина и возможность быстрой смены технологий позволяют работать высшей школе в роли «реактора» компетентных кадров.
Рассмотрим критерий получения высшего образования. Функция хаpaктеризует возможности студента ( при ) и специалиста ( при x>1).
Зависимость I(t) хаpaктеризует действия высшей школы и общества по подготовке специалиста. Рассмотрим взаимодействие этих двух факторов.
Из модели следует, что квалификация будет расти ( ) в данный момент времени, если
(10)
Это необходимое условие эффективного обучения. Оно должно быть выполнено в течении всего времени обучения.
Из уравнения (1) следует, что
Проинтегрируем его по времени обучения:
Если
(11)
то за время учебы студент с начальной подготовкой x0 и возможностями, определяемыми , станет специалистом.
СПИСОК ЛИТЕРАТУРЫ:
- Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. Москва. Изд-во УРСС. 2003. с. 285.
- Ахромеева Т.С., Курдюмов С.П., Малинецкий Г.Г., Самарский А.А. нестационарные структуры и диффузный хаос. М.: наука, 1992.
Работа представлена на научную международную конференцию «Перспективы развития вузовской науки», "Дагомыс" (Сочи), 20-23 сентября 2008 г. Поступила в редакцию 01.10.2008.
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
24 04 2024 7:53:56
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
22 04 2024 17:51:40
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
21 04 2024 10:13:46
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
20 04 2024 23:29:21
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
19 04 2024 3:47:34
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
17 04 2024 15:26:34
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
16 04 2024 3:55:28
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
15 04 2024 2:58:27
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
14 04 2024 2:41:24
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
12 04 2024 20:44:13
 Статья в формате PDF
157 KB...
Статья в формате PDF
157 KB...
11 04 2024 6:38:23
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
10 04 2024 4:14:13
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
09 04 2024 1:46:55
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
08 04 2024 12:50:39
06 04 2024 20:33:27
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
05 04 2024 23:28:35
04 04 2024 12:18:20
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
03 04 2024 21:49:51
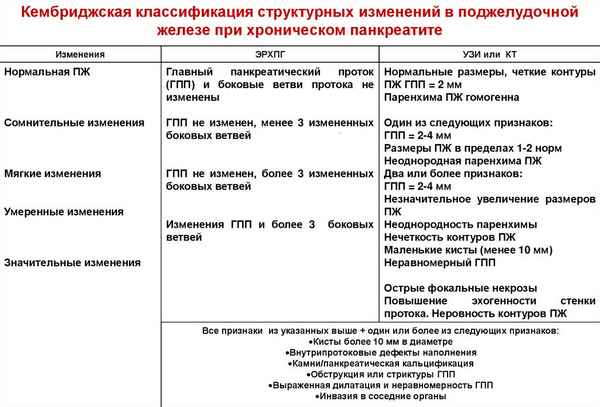 В условиях эксперимента доказано, что острый панкреатит и травма поджелудочной железы приводят к повышению гемоциркуляции в поджелудочной железы. Хроническая алкогольная интоксикация, длительное применение ингибиторов протонной помпы и сочетание этих условий статистически значимо снижают перфузию в поджелудочной железе, желудке и двенадцатиперстной кишке. Для коррекции развившихся изменений рекомендовано применять электромагнитные волны. При этом электромагнитные волны низкой интенсивности частотой 61 Ггц снижают показатели перфузии в органах брюшной полости. Излучение частотой 65 Ггц – увеличивает эти показатели.
...
В условиях эксперимента доказано, что острый панкреатит и травма поджелудочной железы приводят к повышению гемоциркуляции в поджелудочной железы. Хроническая алкогольная интоксикация, длительное применение ингибиторов протонной помпы и сочетание этих условий статистически значимо снижают перфузию в поджелудочной железе, желудке и двенадцатиперстной кишке. Для коррекции развившихся изменений рекомендовано применять электромагнитные волны. При этом электромагнитные волны низкой интенсивности частотой 61 Ггц снижают показатели перфузии в органах брюшной полости. Излучение частотой 65 Ггц – увеличивает эти показатели.
...
02 04 2024 2:40:24
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
01 04 2024 21:22:43
 Приведенные материалы исследования позволяют заключить следующее. Изменения в диссимиляции глюкозы происходят еще до утраты клетками способности образовывать колонии на питательных средах. Уменьшение количества и замедление выхода радиоактивного углекислого газа в НФ холерных вибрионов, вероятно, связано с перестройкой метаболизма, проявляющемся в сдвиге его в сторону гликолиза и разрывом цепей цикла Кребса, хаpaктерным для хемолитоавтотрофов. Пребывание в условиях микрокосмов при низкой температуре индуцирует функционирования цикла Кальвина, что вероятно, обеспечивает клетку необходимыми пластическими материалами и способствует выживанию при отсутствии органических питательных веществ.
...
Приведенные материалы исследования позволяют заключить следующее. Изменения в диссимиляции глюкозы происходят еще до утраты клетками способности образовывать колонии на питательных средах. Уменьшение количества и замедление выхода радиоактивного углекислого газа в НФ холерных вибрионов, вероятно, связано с перестройкой метаболизма, проявляющемся в сдвиге его в сторону гликолиза и разрывом цепей цикла Кребса, хаpaктерным для хемолитоавтотрофов. Пребывание в условиях микрокосмов при низкой температуре индуцирует функционирования цикла Кальвина, что вероятно, обеспечивает клетку необходимыми пластическими материалами и способствует выживанию при отсутствии органических питательных веществ.
...
31 03 2024 3:22:15
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
30 03 2024 13:39:31
 Статья в формате PDF
153 KB...
Статья в формате PDF
153 KB...
28 03 2024 2:28:47
 Статья в формате PDF
267 KB...
Статья в формате PDF
267 KB...
27 03 2024 7:51:49
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
26 03 2024 22:33:36
 При выборочной обработке произрастающих деревьев первым действием всегда является отбор их по качеству древесины. В связи с этим цель статьи – показать методологическую возможность разработки и уточнения системы акустических показателей древесины (САПД) применительно к действиям отбора растущих деревьев для последующей механической обработки древесины.
...
При выборочной обработке произрастающих деревьев первым действием всегда является отбор их по качеству древесины. В связи с этим цель статьи – показать методологическую возможность разработки и уточнения системы акустических показателей древесины (САПД) применительно к действиям отбора растущих деревьев для последующей механической обработки древесины.
...
25 03 2024 19:22:43
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
23 03 2024 1:42:58
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
22 03 2024 4:53:52
 Статья в формате PDF
238 KB...
Статья в формате PDF
238 KB...
21 03 2024 6:37:10
 Рассматриваются психические, социальные и личностные компоненты здоровья. Анализируются различия между медицинской (психиатрической) и психологической моделью психического здоровья. Показано, что концепция «позитивного психического здоровья» подходит для оценки личностного здоровья. Важнейшие критерии личностного здоровья – способность выполнять социальные роли и зрелось личности. Исследование психического здоровья личности осуществляется с помощью психологических методик.
...
Рассматриваются психические, социальные и личностные компоненты здоровья. Анализируются различия между медицинской (психиатрической) и психологической моделью психического здоровья. Показано, что концепция «позитивного психического здоровья» подходит для оценки личностного здоровья. Важнейшие критерии личностного здоровья – способность выполнять социальные роли и зрелось личности. Исследование психического здоровья личности осуществляется с помощью психологических методик.
...
20 03 2024 23:43:41
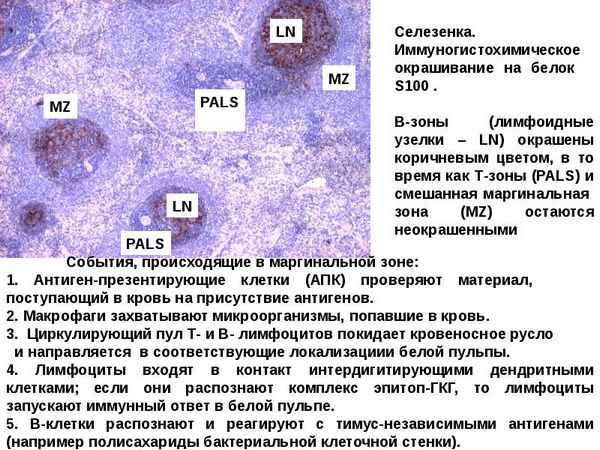
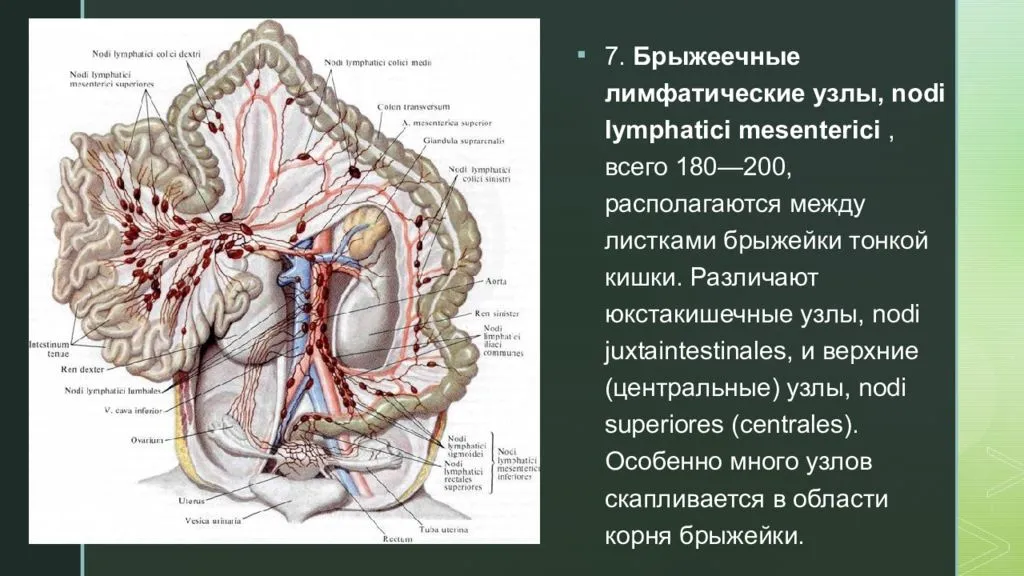 Стромальная закладка краниальных брыжеечных лимфатических узлов происходит у плодов белой крысы 17-18 суток в результате инвaгинации ветвей краниальной брыжеечной и подвздошно-ободочной артерий с окружающей рыхлой соединительной тканью в просвет кишечных лимфатических стволов.
...
Стромальная закладка краниальных брыжеечных лимфатических узлов происходит у плодов белой крысы 17-18 суток в результате инвaгинации ветвей краниальной брыжеечной и подвздошно-ободочной артерий с окружающей рыхлой соединительной тканью в просвет кишечных лимфатических стволов.
...
19 03 2024 11:30:40
 Статья в формате PDF
190 KB...
Статья в формате PDF
190 KB...
18 03 2024 2:54:20
16 03 2024 9:34:10
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::