К ВОПРОСУ ПРОЕКТИРОВАНИЯ МЕТАЛЛИЧЕСКИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ ПОКРЫТИЙ С БОЛТОВЫМИ СОЕДИНЕНИЯМИ ЭЛЕМЕНТОВ
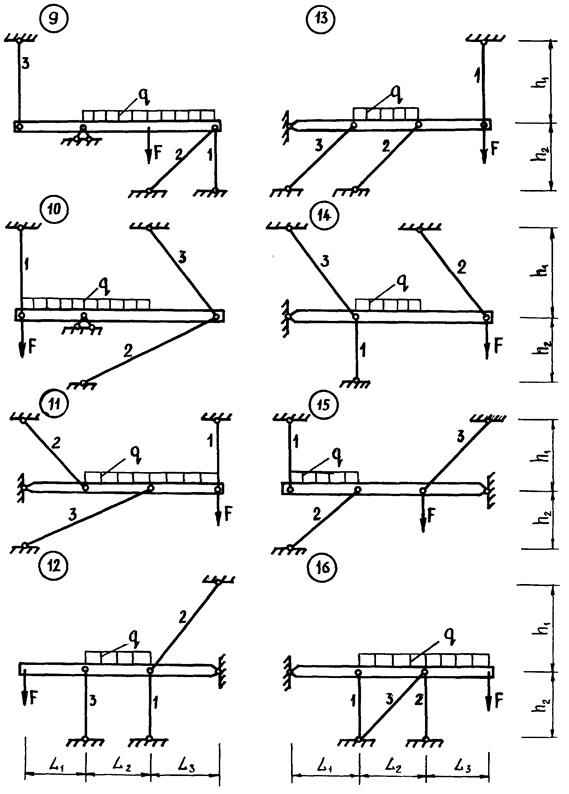
Статически неопределимые системы из металлических конструкций с болтовыми соединениями элементов широко применяются в строительстве. Целесообразность применения металлических конструкций устанавливается на основании технико-экономического анализа конструктивных решений. Таким конструкциям присуще высокая прочность, относительная легкость, технологичность изготовления и монтажа, трaнcпортабельность.
Стремление к увеличению габаритов зданий а, следовательно, и увеличению площади покрытия в промышленных, развлекательных и спортивных сооружениях привело к расширению номенклатуры конструкций с болтовыми соединениями их элементов.
Компоновочные и конструктивные особенности таких элементов позволяют выделить монтируемые с их применением конструкции в особый класс сооружений, отличительными особенностями которых являются:
- перераспределение усилий в статически неопределимых системах вследствие неупругих смещений в соединениях элементов, вызываемых неплотной постановкой болтов в отверстия;
- влиянием на усилие в статически неопределимых системах повышенных деформаций их оснований вследствие неравномерных просадок фундаментов этих сооружений.
О важности учета отмеченных факторов свидетельствуют наблюдавшиеся на пpaктики случаи потери несущей способности элементов, к примеру, надстроек плавучих опор для строительства мостов в результате перераспределений усилий от неучтенных перемещений. Причиной разрушения некоторых покрытий развлекательных сооружений, выполненных из металлических статических неопределимых систем с болтовыми соединениями элементов может быть также по причине неучтенных смещений на величину разности диаметров болта и отверстия и на величину смятия металла в соединении по площадке контакта болта с отверстием. Этим определяется актуальность соответствующих исследований.
Наиболее сложным вопросом расчета статически неопределимых систем является определение усилий в элементах. Решетчатые конструкции с болтовыми соединениями элементов рассчитываются в основном с учетом шарнирного соединения в узлах. При расчете таких конструкций, представляющих собой многократно статически неопределимые стержневые системы, с целью сокращения объема вычислений, часто пользуются приближенными способами, понижающими, а иногда и полностью исключающими степень статической неопределимости.
Выполненный обзор научно-исследовательских работ в области решетчатых каркасных конструкций свидетельствует о существенном влиянии деформативности болтовых соединений на перераспределение внутренних усилий в элементах. Столь значительное влияние смещений в соединениях вынуждает весьма внимательно подходить к проектированию и расчету решетчатых конструкций, элементы которых соединяются на болтах нормальной точности.
Смещение в болтовых соединениях решетчатых конструкций учитываются посредством замены модулей упругости Е на модуль линейной деформации Еэ элементов, определяемые через модули деформаций болтовых соединений в начале и в болтовых i- го элемента.
Модуль деформации болтового соединения при усилии в i-том элементе запишется как:
,
где -- сила трения в соединениях i-го элемента;
-эмпирическая зависимость при работе соединения на смятие [2];
U - сдвиг в соединении на разность номинальных диаметров болта и отверстия;
V - допускаемые отклонения от номинальных диаметров болта и отверстия;
-- неупругая деформация смятия.
Для соединений на высокопрочных болтах, в случае использования последних как несущих, сила трения определяется по формуле:
,
где -- нормативное усилий натяжение болта;
f - коэффициент трения;
B0 , B1 -- эмпирические параметры, значения которых для низколегированной и углеродистой стали, приводятся в таблице [2].
Изменение расстояний между центрами узлов i-го элемента определяется как сумма упругой деформации и
,
или .
Отсюда модуль линейной деформации i-го элемента
.
Допуская, что величины смещений в соединениях в начале и конце i-го элемента одинаковы, модуль деформации элемента будет определяться по формуле:
.
Расчет ведется методом итерации с поэтапным уточнением усилий в элементах статически неопределимых систем. Итерационный процесс можно выполнять, также уточняя напряжения в i-том элементе. В этом случае формула для определения модуля деформации будет иметь вид:
.
В первом приближении значения определяется по напряжениям в конструкции с не смещающимися узлами.
Таким образом, замена модуля упругости на модуль линейной деформации позволит учесть смещения в болтовых соединениях при расчете многократно статически неопределимых систем и избежать перераспределений усилий в элементах, приводящих к разрушению конструкций.
Статья в формате PDF
106 KB...
16 06 2026 23:22:35
Статья в формате PDF
106 KB...
15 06 2026 12:19:48
Статья в формате PDF
122 KB...
14 06 2026 17:41:11
Статья в формате PDF
127 KB...
13 06 2026 7:22:11
Статья в формате PDF
245 KB...
12 06 2026 18:20:13
Статья в формате PDF
105 KB...
11 06 2026 7:35:51
Статья в формате PDF
104 KB...
10 06 2026 5:28:25
Статья в формате PDF
144 KB...
09 06 2026 11:39:48
Статья в формате PDF
228 KB...
08 06 2026 2:42:18
Статья в формате PDF
106 KB...
06 06 2026 8:37:31
Статья в формате PDF
251 KB...
05 06 2026 4:53:27
Статья в формате PDF
334 KB...
04 06 2026 23:43:51
Статья в формате PDF
393 KB...
03 06 2026 14:23:11
Исследования мозговых механизмов пограничных нейрофизиологических расстройств находятся еще в начальной стадии. Следовательно, весьма продуктивно проведение исследование этой проблемы с применением математических методов в определении ценности диагностических тестов, выбора и оценки способов восстановления функций мозговых структур.
...
02 06 2026 6:37:19
Статья в формате PDF
90 KB...
01 06 2026 23:59:58
Статья в формате PDF
1342 KB...
30 05 2026 11:23:36
Статья в формате PDF
107 KB...
27 05 2026 2:42:11
Статья в формате PDF
118 KB...
26 05 2026 19:20:24
Статья в формате PDF
120 KB...
25 05 2026 15:32:10
Статья в формате PDF
111 KB...
24 05 2026 16:22:34
Задачу формирования интеллекта учащихся призвана решать современная школа и, в первую очередь, учебные заведения с названиями «лицей» и «гимназия». В представленной работе излагаются сведения об основных этапах по подготовке и проведению школьной научно-пpaктической конференции «В науку первые шаги», которая ежегодно проводится в Лицее № 37 г. Саратова. В рамках конференции каждый учащийся 11 класса защищает выпускную работу по профильному предмету (математике, физике, информатике, химии, биологии и др.). Подготовка к защите выпускной или творческой работы по химии способствует личностно-ориентированному обучению и воспитанию школьников, развитию активности и самостоятельности, учит работать с библиографической и информационно-справочной литературой, пользоваться электронными каталогами через систему Internet, знакомит с историей науки, развивает экспериментальные навыки, обучает целенаправленным наблюдениям.
...
23 05 2026 0:48:20
Статья в формате PDF
128 KB...
22 05 2026 3:43:38
Статья в формате PDF
255 KB...
21 05 2026 14:16:33
Статья в формате PDF
124 KB...
19 05 2026 3:14:31
Статья в формате PDF
114 KB...
18 05 2026 19:50:22
Статья в формате PDF
107 KB...
17 05 2026 19:16:14
В районе падения отделяющихся частей paкет-носителей и возможного загрязнения нефтепродуктами изучены основные хаpaктеристики и особенности организации лесных сообществ дереворазрушающих грибов в высотно-поясном градиенте.
...
16 05 2026 5:28:45
Общеобразовательный процесс включает в себя множество учебных дисциплин, формирующих мышление учащихся, в том числе и естественнонаучные дисциплины. Гимназическое образование в современной жизни формирует у учащихся личностные качества, ценностные ориентиры, социально значимые знания, отвечающие динамичным изменениям социума и необходимые для организации самостоятельной достойной жизни.
...
15 05 2026 16:40:52
Статья в формате PDF
121 KB...
14 05 2026 20:32:32
Статья в формате PDF
101 KB...
13 05 2026 19:48:53
Статья в формате PDF
126 KB...
12 05 2026 0:58:14
Статья в формате PDF
116 KB...
11 05 2026 23:54:58
Статья в формате PDF
109 KB...
10 05 2026 23:18:30
Статья в формате PDF
84 KB...
09 05 2026 16:47:36
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
