ТЕОРЕМА ЕДИНСТВЕННОСТИ ЗАДАЧИ ТВ ДЛЯ ОБОБЩЕННОГО УРАВНЕНИЯ ТРИКОМИ СО СПЕЦИАЛЬНЫМИ УСЛОВИЯМИ СОПРЯЖЕНИЯ

Уравнение
L(u) = sgn y|y|m uxx + uyy = 0, (1)
m>0, рассмотрим в области D, ограниченной гладкой кривой Г, лежащей в полуплоскости y>0, с концами А(0,0), В(1,0), а в полуплоскости y<0 отрезками хаpaктеристик
,
Введем обозначения D+ = D ∩ {y>0}, D- = D ∩ {y<0}.
Задача Тв. . Найти функцию u(x,y) со свойствами:
1) u(x,y) ∈ C(D);
2) uxx,uyy ∈C(D+ ∪D-);
uy ∈ C(D), L(u) = 0 в D+ ∪D-
3) u(x,y) подчиняется краевым условиям
u|г = φ (s), (2)
s - длина дуги кривой Г, отсчитываемой от точки В.
u|АС = f(x), x ∈ [0; ] (3)
4) u(x,y) подчиняется условию сопряжения
v+(x) = H-(x), x ∈ (0,1), (4)
v+(x) = uy, x ∈ (0,1), (5)
H-(x) = (x - t)-2qv-(t)dt, x ∈ (0,1), (6)
v-(x) = uy, x ∈ (0,1), (7)
Теорема единственности поставленной задачи доказывается с применением утверждений леммы Бабенко [1] и леммы.
Лемма. Если u(x,y) ∈ C(D) - решение уравнения (1) в области D- таково, что u(x,y) = (x) достигает наибольшего положительного (наименьшего отрицательного) значения в точке х0, ∈ (0,1), при этом u|AC = 0 и 2q, то Н- (х0)>0 (H-(x0)<0).
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
16 04 2024 0:55:11
 Статья в формате PDF
689 KB...
Статья в формате PDF
689 KB...
15 04 2024 0:47:35
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
14 04 2024 8:46:26
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
13 04 2024 12:43:36
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
12 04 2024 23:45:34
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
11 04 2024 20:51:16
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
10 04 2024 20:49:43
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
09 04 2024 6:29:49
Статья в формате PDF 235 KB...
08 04 2024 5:16:53
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
07 04 2024 19:19:47
 Статья в формате PDF
1342 KB...
Статья в формате PDF
1342 KB...
06 04 2024 19:40:25
 Статья в формате PDF
256 KB...
Статья в формате PDF
256 KB...
05 04 2024 9:30:55
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
02 04 2024 2:33:49
01 04 2024 19:18:13
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
31 03 2024 4:40:27
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
30 03 2024 12:51:59
 Статья в формате PDF
251 KB...
Статья в формате PDF
251 KB...
29 03 2024 0:55:11
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
28 03 2024 21:20:22
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
27 03 2024 19:33:32
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
26 03 2024 23:14:28
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
25 03 2024 10:13:47
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
24 03 2024 20:56:32
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
22 03 2024 5:10:45
 Статья в формате PDF
284 KB...
Статья в формате PDF
284 KB...
21 03 2024 7:43:52
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
20 03 2024 17:43:17
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
19 03 2024 15:23:12
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
18 03 2024 23:31:24
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
17 03 2024 4:53:14
15 03 2024 7:47:42
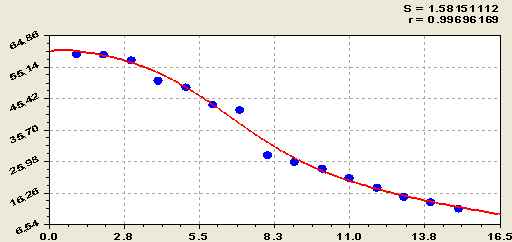 Способ глазомерного учета выхода сортиментов из деревьев лесного древостоя широко применялся в дореволюционное время под названием коммерческая таксация.
Исходя из биотехнического принципа в лесной экономике показана возможность выполнения коммерческой таксации древостоя моделированием стоимостных и возрастных распределений лесных деревьев по текущим рыночным ценам на круглые лесоматериалы.
...
Способ глазомерного учета выхода сортиментов из деревьев лесного древостоя широко применялся в дореволюционное время под названием коммерческая таксация.
Исходя из биотехнического принципа в лесной экономике показана возможность выполнения коммерческой таксации древостоя моделированием стоимостных и возрастных распределений лесных деревьев по текущим рыночным ценам на круглые лесоматериалы.
...
14 03 2024 20:26:37
13 03 2024 0:29:28
12 03 2024 21:49:53
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
11 03 2024 19:36:34
10 03 2024 2:22:20
 Статья в формате PDF
286 KB...
Статья в формате PDF
286 KB...
09 03 2024 22:31:18
08 03 2024 6:14:15
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::