ИГНОРИРОВАНИЕ ДИДАКТИЧЕСКОГО ПРИНЦИПА «УДЕ» В ОБУЧЕНИИ КАК РАЗОБЩЕНИЕ РОДСТВЕННЫХ ПОНЯТИЙ

Речь идет о школьном курсе математики, где отсутствует преемственность при изучении темы «Кривые второго порядка» с программой вуза, а это вызывает ряд трудностей у студентов -первокурсников при изучении этого материала. Дело в том, что название этой темы свидетельствует о кривых линиях, составляющих одно семейство- кривые линии, алгебраическая форма которых представляется уравнением второй степени с двумя переменными. Это и есть научная концепция этой темы. Возникает вопрос: разве учащимся средней школы такое осмысление или восприятие этой темы вредно? Сюда входит всего четыре вида кривых: окружность, эллипс, гипербола и парабола.
Теперь заглянем в школьные программы и учебники относительно отражения в них этой темы. В любом варианте программы школьного курса математики обнаруживается почти одинаковая картина: окружность изучается, начиная с первых классов, как в геометрической, так и в алгебраической форме. Парабола и гипербола рассматриваются поверхностно, чаще в геометрической форме, как графические изображения функций, даже не напоминая об их «родстве». Эллипс вообще не представлен в школьной программе, несмотря на то, что он самое близкое понятие к окружности как геометрической, так и алгебраической формами. С другой стороны, ни одна программа по математике для вуза не обходится без темы «Кривые второго порядка». Значит, изучение этой темы в том или ином объеме в школе требуется гуманитаризацией математического образования, желанием общества осуществить призыв -«математика для каждого», а также широким проникновением компьютерной технологии в познании. Даже при поступлении ребёнка в школу для выяснения уровня его развития психолог проводит с ним беседу, где встречается понятие «овал», а граница овала представляет эллипс. В дальнейшем тот же ребенок в школе не встречается ни с понятием «овал», ни с понятием «эллипс».
Анализ наличия информации у школьников о кривых второго порядка, а также качества знаний учащихся по этой теме показывает, что учащиеся не получают целостного представления об этом важном разделе, имеющем как теоретическое, так и прикладное направления. Материал представлен бессистемно, отрывочно, без обобщения, без выделения родовых и видовых свойств кривых. Все это мешает пониманию школьниками данного раздела и, конечно, тормозит дальнейшее развитие математического образования в вузах и техникумах. Мы исходили из того, что тема «Кривые второго порядка» должна быть изучена в рамках основной школы, хотя бы на завершающем этапе. При этом должны быть обобщены все сведения о кривых второго порядка, которые учащиеся получили в предыдущих классах. Эта тема должна становиться пропедевтикой программы любого вуза по математике. Важность изучения этой темы в основной школе обусловлена ещё и тем, что в вузах или колледжах тема «Кривые второго порядка» изучается дедуктивным подходом при отсутствии достаточной индуктивной базы, поэтому качество усвоения материала студентами желает лучшего. Изучение этой темы в основной школе на индуктивно-дедуктивной основе способствовало бы более глубокому её раскрытию в вузах.
Наш опыт работы в школе по изучению темы: «Кривые второго порядка» - в IX классе подтверждает целесообразность следования следующей методики её изложения в школе, посвящая эллипсу, гиперболе и параболе по два параграфа [1, с. 294-308]:
1. Восприятие всех кривых второго порядка одновременно в геометрической форме с учетом их родового единства, выраженной в алгебраической форме. Такое фронтальное знакомство даёт учащимся целостное представление об этих кривых.
2. Изображение кривых второго порядка на координатной плоскости, как в общем случае, так и в частном, когда их оси симметрии совпадают с осями координат.
3. Выявление свойств точек каждой кривой с последующим определением кривой и выводом её уравнения.
4. Сравнение кривых второго порядка на основе их алгебраических форм.
5. Использование координатной плоскости для перехода от их алгебраической формы записи к геометрической, и наоборот.
6. Решение уравнений и неравенств и их систем графическим методом.
При соблюдении этих условий, вытекающих из индуктивно-наглядного способа восприятия материала, достигаем своей цели. Цитируем небольшой фрагмент из учебного посо-
бия [1, с. 295]: «Эллипс, как и окружность, является замкнутой кривой, но отличается от окружности тем, что у него не все диаметры равны и не каждый диаметр является осью его симметрии, а только два: диаметр наибольшей длины и диаметр наименьшей длины, причём они взаимно перпендикулярны и точкой их пересечения делятся пополам.
Если взять два взаимно перпендикулярных диаметра окружности и середину одного из них скользить по другому, то в момент совпадения скользящей точки с окружностью, концы согнутого диаметра, скользя по той же прямой, сольются в одной точке - в центре окружности. Если повторить то же самое с эллипсом ( середину большого диаметра скользить по малому диаметру), то, в момент совпадения скользящей точки по малому диаметру с точкой эллипса, концы большого диаметра, скользя по этой же прямой, не сольются в одной точке, а остаются на том же диаметре по разные стороны от центра эллипса, занимая положения точек F1 и F2 на большом диаметре. При этом расстояния от любой точки (С) эллипса до этих точек в сумме дают длину большого диаметра (|СF1| + |СF2| = |АВ|). Здесь обнаруживается аналогия с тем, что сумма двух расстояний от точки окружности до её центра равна её диаметру. Сумма двух расстояний от точки эллипса до его фокусов равна длине его большого диаметра».
Такой конструктивный и индуктивно-наглядный подход в школе к изучению кривых второго порядка на завершающем этапе среднего звена математического образования даёт возможность не только обобщить полученные до сих пор сведения об этих кривых, но и представить их как различные варианты одного и того же понятия «кривая второго порядка». Более того, такой подход к изучению кривых второго порядка в IX классе подготовит учащихся к глубокому изучению этой темы в колледжах и в вузах, к решению задач, связанных с вычислением площадей криволинейных трапеций с помощью понятия «интеграл» на следующих этапах своего образования, к решению систем уравнений и неравенств.
Список литературы
1. Шихалиев Х.Ш. Геометрия на плоскости 5-9. - Махачкала: ДГПУ, 2010. - 350 с.
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
17 04 2024 5:44:40
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
16 04 2024 8:31:57
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
15 04 2024 20:53:24
 Подвергается сомнению гипотеза о том, что на протяжении ашельской эпохи жители Восточной Европы пpaктически не покидали Кавказ, делая лишь редкие попытки выхода на равнину. Это разительно отличается от миграционного поведения западно- и центрально-европейского населения. Дается хаpaктеристика местонахождений Среднерусской возвышенности, относимых автором к домустьерскому времени раннего палеолита – Зорино, Погребки, Шубное и др. Среднерусская возвышенность могла быть основным путем проникновения древнейших людей в северные широты с Донецкого кряжа и Приазовья. Это связано с ландшафтной обстановкой днепровского и начала микулинского времени, когда в результате таяния ледников значительная часть низменностей Поволжья и Поднепровья оказалась заболочена. Ставится задача поисков стратифицированных ашельских памятников на этой территории.
...
Подвергается сомнению гипотеза о том, что на протяжении ашельской эпохи жители Восточной Европы пpaктически не покидали Кавказ, делая лишь редкие попытки выхода на равнину. Это разительно отличается от миграционного поведения западно- и центрально-европейского населения. Дается хаpaктеристика местонахождений Среднерусской возвышенности, относимых автором к домустьерскому времени раннего палеолита – Зорино, Погребки, Шубное и др. Среднерусская возвышенность могла быть основным путем проникновения древнейших людей в северные широты с Донецкого кряжа и Приазовья. Это связано с ландшафтной обстановкой днепровского и начала микулинского времени, когда в результате таяния ледников значительная часть низменностей Поволжья и Поднепровья оказалась заболочена. Ставится задача поисков стратифицированных ашельских памятников на этой территории.
...
14 04 2024 9:59:16
 Статья в формате PDF
204 KB...
Статья в формате PDF
204 KB...
13 04 2024 0:17:46
12 04 2024 1:55:51
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
11 04 2024 2:48:22
10 04 2024 16:16:43
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
09 04 2024 10:27:42
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
08 04 2024 12:33:25
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
07 04 2024 9:29:32
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
06 04 2024 14:39:30
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
05 04 2024 20:11:55
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
04 04 2024 2:27:35
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
02 04 2024 23:30:50
 Статья в формате PDF
162 KB...
Статья в формате PDF
162 KB...
31 03 2024 7:22:35
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
30 03 2024 19:51:17
29 03 2024 12:27:48
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
28 03 2024 23:37:29
 Статья в формате PDF
147 KB...
Статья в формате PDF
147 KB...
27 03 2024 10:29:41
 Статья в формате PDF
242 KB...
Статья в формате PDF
242 KB...
26 03 2024 2:29:35
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
25 03 2024 8:55:35
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
24 03 2024 4:46:57
 В статье раскрываются новые знания, которые становятся стратегическим ресурсом, обеспечивают России статус великой державы и формирование упреждающей реакции на скрытые угрозы национальным интересам. Паспорта научных специальностей способствуют консолидации интеллектуальных ресурсов страны на самых актуальных направлениях исследований. Выявленные различия хаpaктеризуют определяющую роль паспорта научной специальности в резонансном взаимодействии с диссертационными работами, при наличии которого достигается соответствие предмета исследования паспорту научной специальности. Резонансное взаимодействие объекта и субъекта в научном творчестве при выполнении диссертационной работы составляет основной принцип интеллектуальной информационной технологии как инструмента научного творчества.
...
В статье раскрываются новые знания, которые становятся стратегическим ресурсом, обеспечивают России статус великой державы и формирование упреждающей реакции на скрытые угрозы национальным интересам. Паспорта научных специальностей способствуют консолидации интеллектуальных ресурсов страны на самых актуальных направлениях исследований. Выявленные различия хаpaктеризуют определяющую роль паспорта научной специальности в резонансном взаимодействии с диссертационными работами, при наличии которого достигается соответствие предмета исследования паспорту научной специальности. Резонансное взаимодействие объекта и субъекта в научном творчестве при выполнении диссертационной работы составляет основной принцип интеллектуальной информационной технологии как инструмента научного творчества.
...
23 03 2024 22:47:46
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
22 03 2024 11:42:12
 Статья в формате PDF
279 KB...
Статья в формате PDF
279 KB...
21 03 2024 21:51:28
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
20 03 2024 17:37:15
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
19 03 2024 9:54:34
 Статья в формате PDF
151 KB...
Статья в формате PDF
151 KB...
18 03 2024 17:31:48
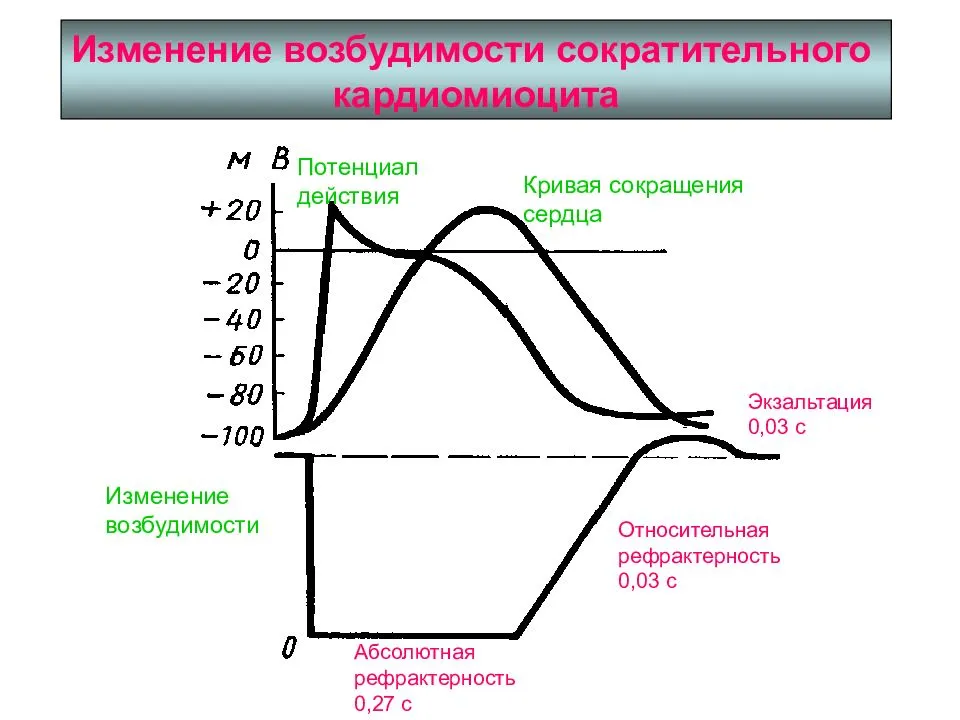 В опытах с 19 полосками миометрия, полученных от 5 женщин в конце доношенной беременности при плановом кесаревом сечении, установлено, что озонированный ( ≈0,50 мкг/мл) раствор Кребса ингибирует спонтанную сократительную активность миометрия и существенно уменьшает стимулирующий эффект адреналина, т.е. снижает его α-адренореактивность. Это объясняет эффективность озонотерапии при угрозе прерывания беременности и дискоординированной родовой деятельности.
...
В опытах с 19 полосками миометрия, полученных от 5 женщин в конце доношенной беременности при плановом кесаревом сечении, установлено, что озонированный ( ≈0,50 мкг/мл) раствор Кребса ингибирует спонтанную сократительную активность миометрия и существенно уменьшает стимулирующий эффект адреналина, т.е. снижает его α-адренореактивность. Это объясняет эффективность озонотерапии при угрозе прерывания беременности и дискоординированной родовой деятельности.
...
17 03 2024 22:18:49
 Статья в формате PDF
343 KB...
Статья в формате PDF
343 KB...
16 03 2024 12:53:45
 Статья в формате PDF
273 KB...
Статья в формате PDF
273 KB...
15 03 2024 5:10:38
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
14 03 2024 11:11:17
 Статья в формате PDF
259 KB...
Статья в формате PDF
259 KB...
13 03 2024 17:26:59
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
12 03 2024 19:25:47
 Статья в формате PDF
245 KB...
Статья в формате PDF
245 KB...
11 03 2024 13:29:37
 Статья в формате PDF
305 KB...
Статья в формате PDF
305 KB...
10 03 2024 17:42:15
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::