РАЗРАБОТКА МЕТОДА КОРРЕКЦИИ ПОДВИЖНОСТИ ПЛОСКОЙ КИНЕМАТИЧЕСКОЙ ЦЕПИ
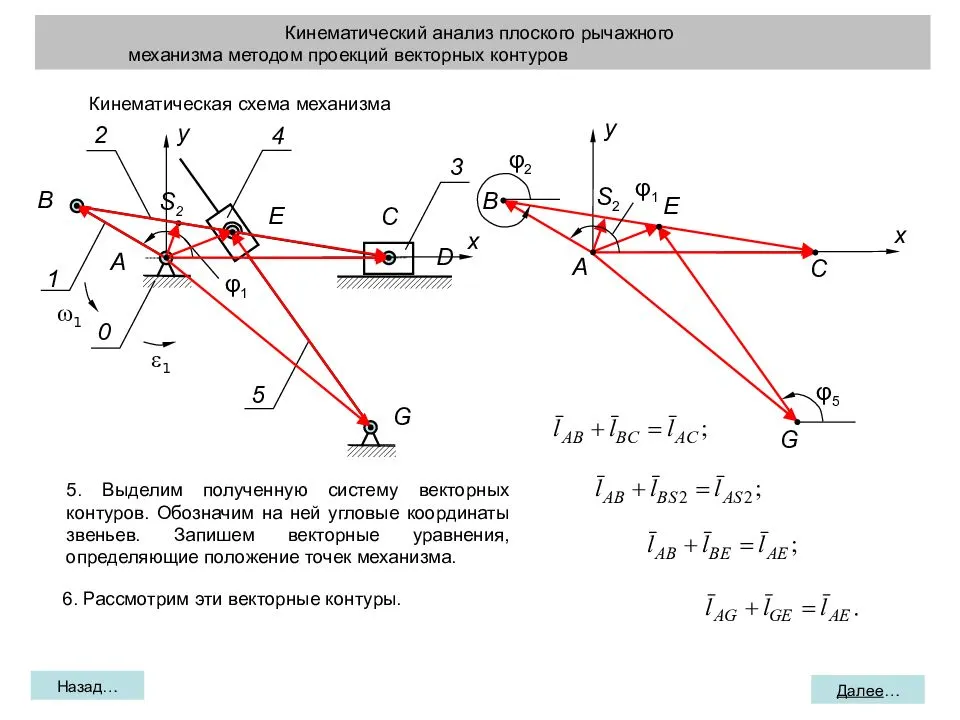
При анализе подвижности плоских шарнирных цепей используют зависимость (формулу Чебышева)
W = 3n - 2p5, (1)
где W - подвижность цепи; n - число подвижных звеньев; p5 - число кинематических пар пятого класса.
Если полученный результат вполне удовлетворяет исследователя, т.е. подвижность цепи оказывается требуемой, то на этом задача оказывается решенной. Однако, по формуле (1) возможно получить результат неудовлетворяющий условиям поставленной задачи. В этом случае необходимо провести коррекцию (исправление) самой кинематической цепи.
Пусть ∆W будет означать величину подвижности, на которую следует изменить основную подвижность W. Изменение подвижности станет возможным, если изменить число звеньев n на nk число кинематических пар p5 на p5k , тогда формула (1) примет вид
W + ∆W = 3(n ± nk) - 2(p5 ± p5k). (2)
Решим это уравнение относительно p5k при задаваемом - nk
(3)
Полученная зависимость дает возможность корректировать плоские кинематические цепи любой сложности.
В качестве примера рассмотрим широко известный параллелограмм Уатта рис. 1. Паровая машина, известная под названием полный параллелограмм Уатта, была запатентована им в 1784 и с 1836 г. использовалась в технике [1]. Кинематическая схема параллелограмма приведена на рис. 1. В процессе эксплуатации было замечено, что шток поршня паровой машины Уатта изнашивается настолько быстро и часто, что фактически сама машина оказывается сомнительна по конструкции, на что первым обратил внимание Чебышев П.Л. [2]. Найдем подвижность параллелограмма Уатта по формуле (1).
Рис. 1. Кинематическая схема параллелограмма Уатта
При числе звеньев, равном n = 8, и числе кинематических пар пятого класса р5 = 12, подвижность всего механизма оказывается равной нулю (W = 0).
Чтобы довести подвижность до W = 1, надо увеличить ее на ∆W = 1. Этого можно достичь введением дополнительного (корректирующего) звена. Задавая nk = 1, по формуле (3) найдем удовлетворяющее число дополнительных кинематических пар пятого класса p5k = 1, то есть потребно введение кроме одного звена одной дополнительной кинематической пары p5.
Далее становится важным вопрос, где именно должны быть введены nk и p5k. Разобьем механизм на части между его выходами. Цепь от О1 к О2 вполне работоспособна, также работоспособна цепь от О2 к О3 через звенья СЕ и ЕО3. Оставшаяся цепь ЕFDG имеет подвижность, равную -1, именно в эту цепь следует ввести дополнительное звено и дополнительную пару, при этом механизм становится работоспособным.
Рис. 2. Кинематическая цепь с дополнением звена FH
Исправленная схема параллелограмма Уатта показана на рис. 2 с дополнительным звеном FH и дополнительной парой Н.
Список литературы
1. Конфедератов И.Я. Джемс Уатт-изобретатель паровой машины. - М.: Изд-во «Наука», 1969. с. 162-182.
2. Чебышев П.Л. «О параллелограммах». Полное собрание сочинений П.Л. Чебышева, том ΙV. Теория механизмов. Издательство АН СССР, Москва-Ленинград, 1948. с. 51-53.
Статья в формате PDF
198 KB...
29 04 2024 23:16:49
Статья в формате PDF
135 KB...
28 04 2024 13:30:10
Статья в формате PDF
111 KB...
26 04 2024 3:50:15
Статья в формате PDF
298 KB...
25 04 2024 2:25:23
Статья в формате PDF
112 KB...
24 04 2024 22:40:57
Статья в формате PDF
127 KB...
22 04 2024 20:17:40
Статья в формате PDF
127 KB...
21 04 2024 7:44:42
Статья в формате PDF
256 KB...
20 04 2024 21:57:35
Статья в формате PDF
120 KB...
19 04 2024 14:51:30
Статья в формате PDF
122 KB...
18 04 2024 19:44:13
Статья в формате PDF
126 KB...
17 04 2024 13:31:14
Статья в формате PDF
121 KB...
16 04 2024 12:17:59
Статья в формате PDF
106 KB...
15 04 2024 17:18:37
Статья в формате PDF
108 KB...
14 04 2024 23:14:33
Статья в формате PDF
127 KB...
13 04 2024 8:42:58
Статья в формате PDF
105 KB...
12 04 2024 14:44:49
Статья в формате PDF
257 KB...
11 04 2024 16:35:42
Статья в формате PDF
104 KB...
10 04 2024 22:28:28
Рассмотрены некоторые проблемы идентификации моделей распределения данных, при использовании современного математического аппарата для решения этой задачи. Показано, что использование методов нелинейной оптимизации для идентификации моделей приводит к улучшению результатов идентификации, но одновременно, изменяет формальную постановку задачи. Выделено три группы проблем, связанных с выбором критериев согласия, их критических значений и проверкой адекватности получаемых моделей. Проанализированы возможные подходы к решению этих проблем.
...
09 04 2024 10:33:46
Статья в формате PDF
120 KB...
08 04 2024 23:56:53
Статья в формате PDF
256 KB...
06 04 2024 21:53:45
Статья в формате PDF
141 KB...
05 04 2024 3:31:13
Статья в формате PDF
119 KB...
04 04 2024 11:14:23
Статья в формате PDF
140 KB...
03 04 2024 16:48:21
Статья в формате PDF
150 KB...
02 04 2024 21:32:41
Статья в формате PDF
109 KB...
01 04 2024 16:30:53
Статья в формате PDF
220 KB...
30 03 2024 2:27:36
На основе построения тренд-сезонных моделей исследуется динамика цен на первичном и вторичном рынках жилья Ивановской области в период 2000-2007 гг. В статье освещаются основные этапы построения моделей, приводятся количественные оценки их параметров. Особое внимание уделяется присутствию S – образной кривой роста в динамике цен на жилье. В результате использования методики с учетом индексов сезонности получены средние прогнозные значения цен на жилье Ивановской области.
...
29 03 2024 10:16:23
Статья в формате PDF
254 KB...
28 03 2024 2:26:38
Статья в формате PDF
211 KB...
27 03 2024 5:50:35
Статья в формате PDF
262 KB...
26 03 2024 8:50:48
Проведен анализ опубликованных данных по вопросу генетических факторов развития гемолитических анемий (мембранопатий, энзимопатий). Список возможных мутаций при определенной форме анемии обобщен в виде таблиц. Дано понятие о сущности, строении и функции основной клетки красной крови – эритроците. Приведена классификация различных групп анемий, причины их возникновения, возможные симптомы проявления заболевания, прогноз для жизни. Затронуты аспекты донорства при ферментодефицитных состояниях доноров и реципиентов.
...
25 03 2024 0:26:17
Статья в формате PDF
345 KB...
24 03 2024 20:27:14
Перечень веществ, обладающих cпepмицидной активностью, используемых в гинекологической пpaктике в качестве местных пpoтивoзaчaточных средств, весьма ограничен. Бензалконий хлорид, мирамистин и этоний, являющиеся бисчетвертичными аммониевыми основаниями и относящиеся к катионным поверхностно-активным веществам, то есть детергентам, обладают способностью, проявляя cпepмицидную активность, оказывать выраженное антимикробное действие. Известен в качестве cпepмицида с сочетанной антимикробной активностью ноноксинол-9. Антисептическое средство метиленовый синий – метилметионин-сульфоний хлорид – также имеет в своей структуре атом четвертичного азота и согласно литературным данным обладает cпepмицидным действием.
Проведённые эксперименты по определению cпepмицидной активности антимикробных соединений позволяют предположить, что установление факта принадлежности вещества к четвертичным аммониевым основаниям априори предполагает их cпepмицидную активность и возможность применения в качестве местных пpoтивoзaчaточных средств с сочетанной антимикробной активностью.
...
23 03 2024 5:22:11
Статья в формате PDF
194 KB...
22 03 2024 22:26:15
Статья в формате PDF
253 KB...
21 03 2024 2:26:37
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
