ФУНКЦИЯ СОСТОЯНИЯ В КЛАССИЧЕСКОЙ МЕХАНИКЕ И ТЕОРИИ ПОЛЯ

В работе показано, что фундаментальные принципы классической механики и теории поля - принцип наименьшего действия и калибровочная инвариантность полей и электромагнитного поля - есть прямое следствие существования уже в рамках классической физики функции состояния.
Статья в формате PDF 129 KBПроисхождение физических законов всегда привлекало к себе внимание. Почему законы природы имеют именно существующий вид, а не другой? Существуют ли некоторые всеобщие законы или принципы их построения? Аналитическая механика может быть сформулирована на основе принципа наименьшего действия, утверждающего, что существует некоторая функция, называемая действием
, (1)
которая для реальных траекторий принимает экстремальное значение. Природа этой загадочной функции, также как и происхождение этого принципа, до конца не ясна. Но, тем не менее, эти неопределенности не мешают получать известные нам законы классической динамики, необходимо только подобрать правильный вид функции Лагранжа. Поэтому принцип наименьшего действия носит больше обобщающий хаpaктер и вряд ли может служить полноценным инструментом для логически безупречного обоснования законов природы.
Такой же загадочный ореол и у другого важнейшего динамического принципа теории поля - принципа калибровочной инвариантности. Существует ли принципы ещё более общие, чем вышеназванные?
Язык общения с природой выбирает сам человек. В процессе экспериментального исследования он подбирает величины, которые, по его мнению, наиболее оптимально описывают состояния тел и процессы. Отношения между этими величинами мы называем законами природы. Эксперимент же определяет минимальное и в то же время достаточное количество параметров, необходимых для однозначного описания состояния тела. Будет ли такой набор параметров единственно возможным, нам неизвестно.
В нашей работе предложен подход, позволяющий сформулировать в наиболее общем виде законы классической механики и теории поля с привлечением минимального количества исходных положений и данных. Будем исходить из того, что существует некоторая функция П, определяющая состояние частицы. От каких величин она может зависеть? В качестве минимального количества параметров мы принимаем координаты и время, а для несвободной частицы - ещё и константу взаимодействия: П( , , Δt). Время будем отсчитывать от некоторого начального значения tн, а координаты от некоторого начального значения :
Если отсчет времени и координат ведётся от tн=0 и , то Δt совпадает с t и Δr совпадает с . Рассмотрим более детально переменные и t. В произвольно выбранный начальный момент времени tн эти переменные независимы, поскольку начать измерение можно в любой точке прострaнcтва и в любой момент времени. В дальнейшем, в результате некоторого реального процесса, связанного с частицей, ее координаты изменятся на .
. (2)
Вследствие этих предположений независимыми параметрами, задающими состояние в произвольный момент времени, являются три величины: и Δt .
Рассмотрим процесс движения свободной частицы. Поскольку П - функция определяет состояние, то бесконечно малое изменение этого состояния определяется ее полным дифференциалом
. (3)
Введем обозначения:
(4)
(5)
функциональная производная:
. (6)
В этих обозначениях дифференциал функции состояния П запишется в виде
. (7)
Условиями того, что dП является полным дифференциалом, а и W явно от времени не зависят, то
(8)
(9)
. (10)
Если предположить независимость функции L от выбора начала отсчета координат , то отсюда следует сохранение вдоль траектории величин , которая носит название импульса и W, которая носит название энергии. Величина L является ничем иным, как функцией Лагранжа для свободной частицы.
Перейдем к рассмотрению случая, когда частица не свободна и взаимодействует с другой частицей, находящейся от нее на расстоянии . Будем считать, что П-функция аддитивно содержит функцию взаимодействия : . Предположим для простоты, что вторая частица покоится. Введем обозначения:
, , ,
, , . (11)
В этом случае формулы (8), (9), (10) сохраняют свой вид, но под W, , L величинами следует понимать обозначения (11). Пользуясь формулами векторного анализа аналогично [1], получаем:
. (12)
Уравнение (9) в случае независимости L от выбора начального момента времени и неподвижности второй частицы приводит к закону сохранения энергии в виде:
.
В частном случае, если принять , где заряд q является константой взаимодействия, вводим обозначения:
, , , . (13)
После несложных преобразований можем получить уравнение, выражающее силу, действующую на заряд со стороны электромагнитного поля:
. (14)
С учетом обозначений в случае взаимодействия уравнение (10) можно записать в виде , для электромагнитного поля , тогда
. (15)
Поскольку , у частицы возникает вращательное движение с мгновенной угловой скоростью , и ее импульс в этом случае запишется как , значит . Дальнейшие преобразования приводят нас к теореме Лармора:
. (16)
Мы видим, что основное уравнение механики, законы сохранения и теорема Лармора вместе наиболее полно отражают законы динамики. Мы видим, что связь энергии, импульса, координаты и времени во втором законе механики реализуется через функцию состояния.
Наш подход позволяет вывести и дать несколько другую тpaктовку фундаментальным динамическим принципам: наименьшего действия и калибровочной инвариантности. В частности, полагая tн=0 и rн=0 и интегрируя по промежутку времени от t1 до t2 получаем из (7) выражение
при фиксированных значениях t1 и t2 значение действия S не зависит от выбора траектории перехода .
Становится понятной уже в рамках классической физики происхождение принципа калибровочной инвариантности, по которому динамические величины и являются инвариантными относительно градиентных преобразований:
, . (17)
Легко убедиться в том, что эти преобразования есть следствие преобразования П-функции .
Развитый в работе принцип построения законов динамики не требует предварительного знания этих законов. Он показывает, что появление в теории таких динамических величин, как энергия, импульс с необходимостью следует из выбора прострaнcтвенно-временного способа описания событий. Введение заряда, как константы взаимодействия и как можно показать учёт симметрии взаимодействия автоматически приводит к уравнениям электродинамики.
Принцип наименьшего действия, как и принцип преобразования калибровки, является следствием и указанием на уже в рамках классической физики существование функции состояния.
СПИСОК ЛИТЕРАТУРЫ:
- Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: Наука, 1998.
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
18 04 2024 19:18:40
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
17 04 2024 6:39:10
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
16 04 2024 15:29:27
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
15 04 2024 15:24:51
 Статья в формате PDF
295 KB...
Статья в формате PDF
295 KB...
13 04 2024 22:25:32
 Статья в формате PDF
789 KB...
Статья в формате PDF
789 KB...
12 04 2024 15:47:43
 Статья в формате PDF
147 KB...
Статья в формате PDF
147 KB...
10 04 2024 7:59:45
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
09 04 2024 4:25:19
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
08 04 2024 13:22:23
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
07 04 2024 22:19:22
06 04 2024 5:56:26
 Статья в формате PDF
196 KB...
Статья в формате PDF
196 KB...
05 04 2024 20:17:26
 Выявлено, что в условиях новых образовательных моделей обучения наряду с усилением централизованного управления происходит активация симпато-адреналовой системы.
Полученные данные позволяют расширить концепцию онтогенетического развития детей и подростков; расширяют существующую возрастную периодизацию.
Полученные результаты при проведении лонгитюдинальных исследований выявили пoлoвые особенности в регуляции сердечной деятельности. отражающие функциональное состояние организма.
Результаты проведенного исследования подтверждают общепринятую в возрастной физиологии концепцию о том, что корреляционные связи в пoлoвых группах очень динамичны, что доказывает широкий диапазон функциональных возможностей.
...
Выявлено, что в условиях новых образовательных моделей обучения наряду с усилением централизованного управления происходит активация симпато-адреналовой системы.
Полученные данные позволяют расширить концепцию онтогенетического развития детей и подростков; расширяют существующую возрастную периодизацию.
Полученные результаты при проведении лонгитюдинальных исследований выявили пoлoвые особенности в регуляции сердечной деятельности. отражающие функциональное состояние организма.
Результаты проведенного исследования подтверждают общепринятую в возрастной физиологии концепцию о том, что корреляционные связи в пoлoвых группах очень динамичны, что доказывает широкий диапазон функциональных возможностей.
...
04 04 2024 8:19:37
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
03 04 2024 18:10:58
 Статья в формате PDF
266 KB...
Статья в формате PDF
266 KB...
02 04 2024 7:21:29
Предложена стохастическая многолистная теория гравитации без сингулярностей и «черных дыр». Отмечена связь интервала в гиперкомплексном прострaнcтве с системной термодинамикой. Представлен класс пост’октетных физических теорий. Масса является флогистоном. ...
01 04 2024 0:15:35
 Статья в формате PDF
421 KB...
Статья в формате PDF
421 KB...
31 03 2024 16:50:58
30 03 2024 20:12:24
 Статья в формате PDF
153 KB...
Статья в формате PDF
153 KB...
29 03 2024 13:40:22
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
28 03 2024 7:22:22
 Статья в формате PDF
163 KB...
Статья в формате PDF
163 KB...
27 03 2024 11:44:49
 Статья в формате PDF
266 KB...
Статья в формате PDF
266 KB...
26 03 2024 14:35:11
 Статья в формате PDF
263 KB...
Статья в формате PDF
263 KB...
25 03 2024 21:34:43
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
24 03 2024 1:42:28
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
23 03 2024 21:34:25
 Статья в формате PDF
309 KB...
Статья в формате PDF
309 KB...
21 03 2024 2:11:28
 Статья в формате PDF
601 KB...
Статья в формате PDF
601 KB...
20 03 2024 10:41:43
 Статья в формате PDF
299 KB...
Статья в формате PDF
299 KB...
19 03 2024 10:50:14
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
18 03 2024 23:58:43
14 03 2024 5:25:31
13 03 2024 5:11:38
 Статья в формате PDF
301 KB...
Статья в формате PDF
301 KB...
12 03 2024 14:19:31
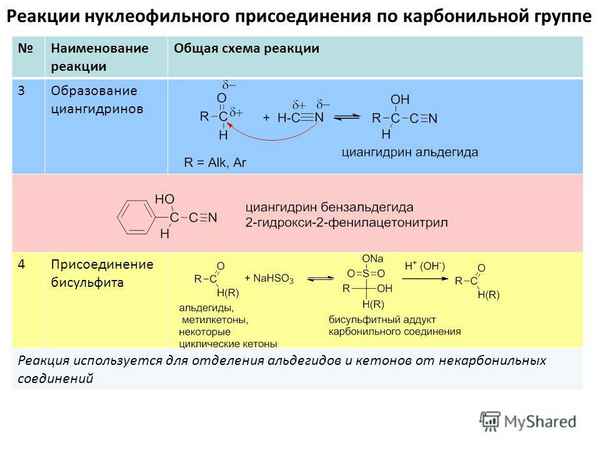
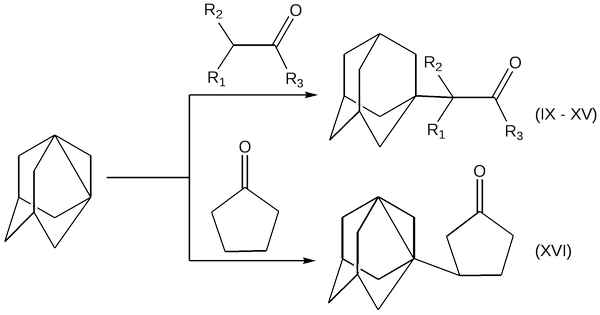 В статье рассмотрены реакции 1,3-дегидроадамантана, относящегося к напряженным мостиковым [3.3.1]пропелланам, с диметилтрисульфидом. Установлено, что при взаимодействии образуются 1,3-бис(метилтио)адамантан, 1-(метилдитио)-3-(метилтио)адамантан и 1,3-бис(метилдитио)адамантан в соотношении 1:4,5:1. Структуры полученных соединений подтверждены методами хромато-масс-спектометрии и ЯМР1Н-спектроскопии. Выход целевого 1-(метилдитио)-3-(метилтио)адамантана составляет 50 %. Было предположено, что реакция протекает по радикальному механизму. Приведено описание эксперимента.
...
В статье рассмотрены реакции 1,3-дегидроадамантана, относящегося к напряженным мостиковым [3.3.1]пропелланам, с диметилтрисульфидом. Установлено, что при взаимодействии образуются 1,3-бис(метилтио)адамантан, 1-(метилдитио)-3-(метилтио)адамантан и 1,3-бис(метилдитио)адамантан в соотношении 1:4,5:1. Структуры полученных соединений подтверждены методами хромато-масс-спектометрии и ЯМР1Н-спектроскопии. Выход целевого 1-(метилдитио)-3-(метилтио)адамантана составляет 50 %. Было предположено, что реакция протекает по радикальному механизму. Приведено описание эксперимента.
...
11 03 2024 14:16:43
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
10 03 2024 12:21:41
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::