К ОЦЕНИВАНИЮ ПАРАМЕТРОВ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ С ПОСТОЯННЫМИ ПРОПОРЦИЯМИ
Общеизвестно, что методы математического моделирования весьма эффективны при решении широкого круга проблем, возникающих в самых различных отраслях знаний. Математические конструкции, содержащиеся в соответствующих моделях, часто имеют существенно нелинейные формы. Одной из таких форм, особенно популярной в экономико-математических моделях, является так называемая кусочно-линейная функция, или производственная функция с постоянными пропорциями:
, , (1)
где xi, y - входные и выходная переменные, , - подлежащие оцениванию параметры, εk - ошибки аппроксимации, n - длина выборки.
Замечательным свойством аппроксимирующей функции (1) является то, что значение выходного фактора , обычно тpaктуемого как выпуск продукции, определяется значением лимитирующего входного фактора. При этом любое наращивание других факторов не приводит к возрастанию выпуска.
В докладе будет доказано, что задача определения неизвестных значений параметров кусочно-линейной функции (1) по методу наименьших модулей (т.е. посредством минимизации суммы абсолютных значений ошибок εk) может быть сведена к задаче частично булевого линейного программирования.
Статья в формате PDF
254 KB...
24 04 2024 21:54:34
Статья в формате PDF
255 KB...
23 04 2024 19:37:54
Статья в формате PDF
102 KB...
22 04 2024 23:39:14
Статья в формате PDF
243 KB...
20 04 2024 0:23:14
Статья в формате PDF
103 KB...
19 04 2024 13:39:11
Статья в формате PDF
289 KB...
17 04 2024 18:10:38
Статья в формате PDF
255 KB...
15 04 2024 7:12:29
Статья в формате PDF
112 KB...
14 04 2024 23:33:57
Статья в формате PDF
124 KB...
13 04 2024 18:32:21
Разработан способ производства хлеба из целого зерна. Снижение микробиологической обсеменненности зерна осуществляется с помощью природных консервантов, которые можно вносить на стадии замачивания зерна или приготовления теста. Для повышения качества хлеба, сокращения продолжительности замачивания зерна, повышения степени его дисперсности при получении теста целесообразно использовать цитолитические ферментные препараты. ...
12 04 2024 17:52:17
Статья в формате PDF
117 KB...
11 04 2024 16:18:53
Статья в формате PDF
111 KB...
10 04 2024 4:47:28
Статья в формате PDF
140 KB...
09 04 2024 11:11:14
Статья в формате PDF
353 KB...
08 04 2024 6:27:47
Статья в формате PDF
132 KB...
07 04 2024 14:34:45
Статья в формате PDF
133 KB...
06 04 2024 5:35:46
Статья в формате PDF
110 KB...
05 04 2024 2:38:42
Статья в формате PDF
307 KB...
04 04 2024 14:55:39
Статья в формате PDF
133 KB...
03 04 2024 1:34:36
Статья в формате PDF
319 KB...
01 04 2024 16:11:43
Статья в формате PDF
255 KB...
31 03 2024 14:41:36
Статья в формате PDF
113 KB...
30 03 2024 1:22:49
Статья в формате PDF
99 KB...
29 03 2024 21:13:59
Статья в формате PDF
124 KB...
28 03 2024 1:46:41
Статья в формате PDF
305 KB...
27 03 2024 2:29:28
Статья в формате PDF
113 KB...
26 03 2024 18:34:58
Статья в формате PDF
111 KB...
25 03 2024 17:37:47
Статья в формате PDF
100 KB...
24 03 2024 10:36:23
Статья в формате PDF
108 KB...
23 03 2024 5:22:57
Статья в формате PDF
172 KB...
22 03 2024 20:39:41
Статья в формате PDF
130 KB...
21 03 2024 8:15:28
Статья в формате PDF
82 KB...
20 03 2024 3:58:39
Статья в формате PDF 231 KB...
18 03 2024 21:59:28
Статья в формате PDF
239 KB...
17 03 2024 20:18:57
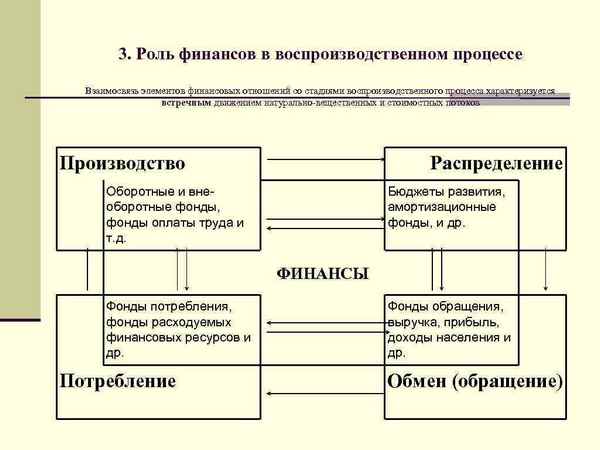Основным направлением совершенствования межбюджетных отношений является достижение сбалансированности бюджетов различных уровней, что, в свою очередь, позволит регионам активно используя потенциал всех форм собственности, иметь самостоятельную базу финансовых ресурсов как основу саморазвития и самообеспечения воспроизводственного процесса.
...
16 03 2024 21:22:34
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
