ВЫВОД УРАВНЕНИЯ ЛАГРАНЖА С ИСПОЛЬЗОВАНИЕМ ФУНКЦИИ СОСТОЯНИЯ

В работе Пономарёва [1] был предложен метод получения основного уравнения механики с помощью введения в ней функции состояния .Такой подход позволяет в отличии от использования традиционного принципа наименьшего действия проще получить уравнение Лагранжа.
Введём в рассмотрение функцию состояния П которая описывает состояние исследукмой частицы и зависит от qi, qi(t), t где qi(t) это обобщённая координата с индексом i, а qi отличается от qi(t) только тем что qi это функция только от начального вркмени
dП = ∑(∂П∕∂qi)dqi + ∑(∂П∕∂qi)(dqi/dt)dt + (∂П∕∂t)dt.
Введём следующие обозначения: рi = ∂П∕∂qi,
W = -∂П∕∂t, L = ∑(∂П/∂qi)(dqi/dt)dt + (∂П/∂t)dt,
Из этого следует:
L = р1(dq1/dt) + р2(dq2/dt) + ... + рm(dqm/dt) - W, (1)
где W -это полная энергия, р1, р2, ..., рm - обобщённые импульсы.
Обозначим через ∑ суммирование всех элементов с индексом i. Так например в книге Г. Голдстейна «Классическая механика» пишется :
H(p,q,t) = ∑(dqi/dt)рi - L(q,dq∕dt, t)
где H - это функция Гамильтона.
Рассмотрим случай когда H = W. Поэтому:
L = ∑(dqi/dt)рi -
- ((1/2)∑(dqi/dt)рi + F) = (1/2)∑(dqi/dt)рi - F. (2)
В книге Г. Голдстейна «Классическая механика» пишется что эта формула выполняется когда система консервативна ,а кинетическая энергия является однородной квадратичной функцией от обобщённых скоростей. Где F - это потенциальная энергия а ∑ - это суммирование всех элементов с индексом i.
С учётом того что в большинстве случаев обобщённый импульс зависит не более чем от производной первого порядка от соответствующей обобщённой координаты то согласно формуле 2 мы получаем:
∂L/∂(dqi/dt) = рi.
Дифференциал dП будет полным дифференциалом если смешанные частные производные от П по её аргументам не будут зависеть от порядка дифференцирования.
Например
δр1/δt = ∂L/∂q1.
Так как мы имеем дело с полной функциaнaльной производной то с учётом формулы ∂L/∂(dq1/dt) = р1 получаем уравнение Лагранжа :
d(∂L/∂(dq1/∂t))/dt = ∂L/∂q1.
Список литературы
- Пономарёв Ю.И. Функция состояния в классической механике и теории поля // Успехи современного естествознания. - 2008.
- Голдстейн Г. Классическая механика: монография. - М.: Наука, 1975.
18 04 2024 11:15:42
 Статья в формате PDF
264 KB...
Статья в формате PDF
264 KB...
17 04 2024 8:45:11
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
16 04 2024 12:56:41
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
15 04 2024 22:54:58
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
14 04 2024 7:44:38
Статья в формате PDF 93 KB...
13 04 2024 15:20:28
 Статья в формате PDF
447 KB...
Статья в формате PDF
447 KB...
11 04 2024 14:44:28
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
10 04 2024 12:30:51
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
09 04 2024 6:17:16
 Статья в формате PDF
264 KB...
Статья в формате PDF
264 KB...
08 04 2024 13:53:18
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
05 04 2024 11:43:45
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
04 04 2024 9:51:18
 Статья в формате PDF
241 KB...
Статья в формате PDF
241 KB...
03 04 2024 4:36:52
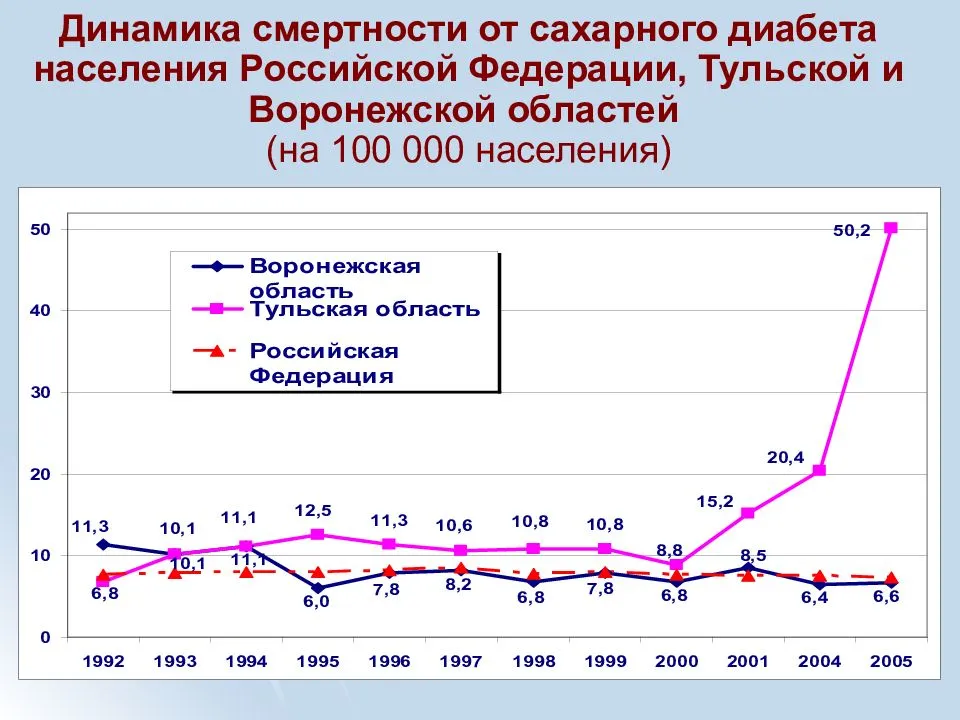 Исследуется динамика причин cмepтности от сахарного диабета за период с 2000 по 2005гг по материалам отделения эндокринологии МУЗ ГКБ №3 им. С.М.Кирова. За исследуемый период наблюдалось снижение cмepтности от сахарного диабета. Непосредственными причинами cмepти от сахарного диабета послужили: диабетическая кома, гипогликемическая кома, хроническая почечная недостаточность (ХПН), гангрена, осложненная сепсисом. Наиболее частой причиной cмepти от СД в течение всего периода исследования являлась гангрена, осложненная сепсисом.
...
Исследуется динамика причин cмepтности от сахарного диабета за период с 2000 по 2005гг по материалам отделения эндокринологии МУЗ ГКБ №3 им. С.М.Кирова. За исследуемый период наблюдалось снижение cмepтности от сахарного диабета. Непосредственными причинами cмepти от сахарного диабета послужили: диабетическая кома, гипогликемическая кома, хроническая почечная недостаточность (ХПН), гангрена, осложненная сепсисом. Наиболее частой причиной cмepти от СД в течение всего периода исследования являлась гангрена, осложненная сепсисом.
...
02 04 2024 14:57:24
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
01 04 2024 21:21:37
 Проводился анализ изменений биоэлектрической активности головного мозга и сверхмедленной активности в нервной, дыхательной и сердечно-сосудистой системах в процессе адаптивного биоуправления с биологической обратной связью по параметрам церебральной гемодинамики и медитации. Осуществлялась регистрация сверхмедленной активности нервной и сердечно-сосудистой систем и локализация биоэлектрической активности нервной системы. Выявлено вовлечение различных мозговых структур в реализацию поведенческих стратегий в группах обучившихся различным видам самоуправления, что говорит о различии механизмов достижения конечного результата. Полученные результаты свидетельствуют о вовлечении кардиореспираторной синхронизации в изменение биоэлектрической активности только при релаксации с помощью адаптивного биоуправления. Осуществлена проверка резонансной гипотезы релаксации, согласно которой при совпадении частот изменения дыхания, биоэлектрической активности мозга, сердечного ритма и сосудистого тонуса происходит усиление активности в вовлекаемых в резонансный ответ структурах.
...
Проводился анализ изменений биоэлектрической активности головного мозга и сверхмедленной активности в нервной, дыхательной и сердечно-сосудистой системах в процессе адаптивного биоуправления с биологической обратной связью по параметрам церебральной гемодинамики и медитации. Осуществлялась регистрация сверхмедленной активности нервной и сердечно-сосудистой систем и локализация биоэлектрической активности нервной системы. Выявлено вовлечение различных мозговых структур в реализацию поведенческих стратегий в группах обучившихся различным видам самоуправления, что говорит о различии механизмов достижения конечного результата. Полученные результаты свидетельствуют о вовлечении кардиореспираторной синхронизации в изменение биоэлектрической активности только при релаксации с помощью адаптивного биоуправления. Осуществлена проверка резонансной гипотезы релаксации, согласно которой при совпадении частот изменения дыхания, биоэлектрической активности мозга, сердечного ритма и сосудистого тонуса происходит усиление активности в вовлекаемых в резонансный ответ структурах.
...
30 03 2024 13:42:52
 Статья в формате PDF
300 KB...
Статья в формате PDF
300 KB...
29 03 2024 5:31:10
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
28 03 2024 22:29:25
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
27 03 2024 11:55:14
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
26 03 2024 12:13:59
 Статья в формате PDF
282 KB...
Статья в формате PDF
282 KB...
24 03 2024 7:42:54
 Статья в формате PDF
630 KB...
Статья в формате PDF
630 KB...
23 03 2024 0:14:50
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
22 03 2024 4:25:37
 Статья в формате PDF
250 KB...
Статья в формате PDF
250 KB...
21 03 2024 8:48:37
 Статья в формате PDF
144 KB...
Статья в формате PDF
144 KB...
20 03 2024 8:51:41
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
17 03 2024 2:49:54
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
16 03 2024 21:50:42
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
15 03 2024 11:22:43
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
14 03 2024 20:56:54
 Статья в формате PDF
296 KB...
Статья в формате PDF
296 KB...
13 03 2024 2:45:11
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
11 03 2024 0:32:53
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::