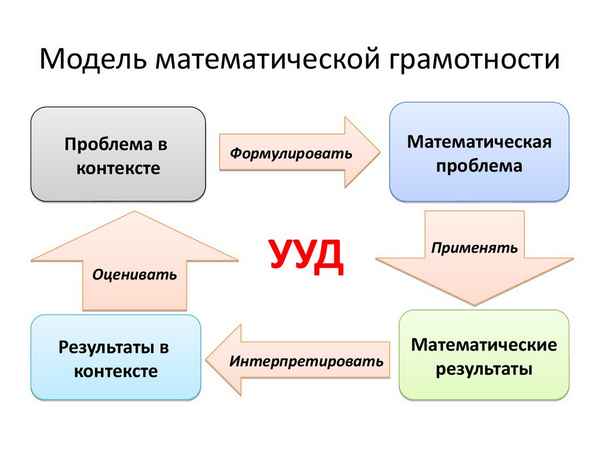
МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ КАК УСЛОВИЕ РАЗВИТИЯ ОБЩЕСТВА
Условия нашего времени таковы, что происходит быстрая смена технологий. Происходит увеличение техногенной составляющей в жизни и профессиональной деятельности каждого человека. Поэтому возрастает значение полноценной математической подготовки каждого выпускника школы, а не только будущего специалиста. Корректируются и цели преподавания математики. Они должны соответствовать разнообразным аспектам самой математики, личным свойствам, которые развивает как изучение ее дисциплин, так и ее пpaктическое применение.
Преобладающее значение необходимо уделить функциональному (утилитарному) аспекту. Утилитарные цели - это усвоение материала прагматической природы, необходимого для грамотного поведения и ориентации в современном мире, для пpaктической жизни (необходимые знания, относящихся к вычислению, геометрическим представлениям, формулам, функциям, графикам, диаграммам, таблицам). Эти основные понятия необходимы для понимания окружающей природы, а также вопросов экономических и общественных. Другой целью преподавания математики в школе является подготовка к последующему изучению научных и технических дисциплин, в которых роль математики непрестанно возрастает, т.е. ученик должен быть «вооружен» сведениями, необходимыми для уверенного продолжения обучения на последующих этапах. Кроме этих целей, можно назвать еще воспитательные и культурные: развитие интеллекта, формирование хаpaктера и общей культуры, воспитание в человеке способности понимать смысл поставленной перед ним задачи. Среди интеллектуальных свойств, развиваемых математикой, наиболее часто упоминаются те, которые относятся к логическому мышлению: дедуктивное рассуждение, способность к абстрагированию, обобщению, способность анализировать, критиковать. Математические упражнения содействует приобретению рациональных качеств мысли и ее выражения: порядок, точность, ясность, сжатость. Они требуют воображения и интуиции, дают чувство объективности, интеллектуальную честность, вкус к исследованию. Изучение математики требует постоянного напряжения внимания, настойчивости, способности сосредоточиться, то есть выполняет важную роль как в развитии интеллекта, так и в формировании хаpaктера. Основным моментом воспитательной функции математики служит приучение к полноценности аргументации. В математике аргументация, не обладающая хаpaктером полной, абсолютной исчерпанности, оставляющая хотя бы малейшую возможность обоснованного возражения, признается ошибочной. А логическая полноценность аргументации - залог успеха в любой дискуссии.
Математика представляет собой культурную ценность сама по себе. Она - идеал формальной красоты, заложенной в произведениях искусства. Этот идеал выражается словами: мера, отношение, порядок, пропорция, являющимися математическими терминами. С выдающейся культурной ценностью математики может сравниться лишь ценность ее как орудия воздействия на реальный мир. Если не всякий человек может достигнуть высокой математической культуры, то всякий нуждается в пpaктической математике. Вслед за естественными науками «математизируются» и науки гуманитарные. Незнание и непонимание математического языка становится помехой развития общества. Знание математического языка - условие экономического существования и элемент безопасности.
СПСИОК ЛИТЕРАТУРЫ:
- В.И.Арнольд, Математика и математическое образование,М,:, Фазис, 2000 г, с.197
- А.- И. Марроу, «История воспитания в античности (Греция)».- М.:, 1998, с.108-112.
Статья в формате PDF
113 KB...
22 07 2026 19:44:13
Статья в формате PDF
196 KB...
21 07 2026 6:51:23
Статья в формате PDF
91 KB...
20 07 2026 10:51:50
Статья в формате PDF
86 KB...
19 07 2026 19:44:28
Статья в формате PDF
116 KB...
18 07 2026 0:18:44
Статья в формате PDF
115 KB...
17 07 2026 8:44:51
Статья в формате PDF
119 KB...
16 07 2026 9:54:19
Статья в формате PDF
268 KB...
15 07 2026 6:55:27
Статья в формате PDF
110 KB...
13 07 2026 2:45:41
Статья в формате PDF
120 KB...
12 07 2026 12:29:42
Статья в формате PDF
111 KB...
11 07 2026 2:42:23
Статья в формате PDF
111 KB...
10 07 2026 10:53:45
Статья в формате PDF
106 KB...
09 07 2026 21:29:28
Статья в формате PDF
105 KB...
05 07 2026 8:28:27
Статья в формате PDF
311 KB...
04 07 2026 0:27:40
Статья в формате PDF
206 KB...
02 07 2026 7:44:22
Статья в формате PDF
297 KB...
01 07 2026 13:19:55
Статья в формате PDF
110 KB...
30 06 2026 8:47:24
Статья в формате PDF
119 KB...
29 06 2026 10:17:35
Статья в формате PDF
116 KB...
28 06 2026 4:55:40
Цель: Изучить функцию бронхо-легочного аппарата и клинико-лабораторных показателей в условиях применения противовоспалительных, антиоксидантных и антигипоксантных препаратов.
Материалы и методы: Обследовали 62 больных АС до лечения и на фоне медикаментозной терапии. Провели 10 дневную терапию актовегином в суточной дозе 200 мг (5 мл). Определили клинико-лабораторные показатели и параметры ФВД, ПСВ%.
Результаты: Выявлены изменения клинико лабораторных показателей, параметров ФВД, ПСВ и улучшение этих показателей на фоне терапии актовегином.
Заключение: Лечение антиоксидантными и антигипоксантными препаратами (актовегин) способствует улучшению функциональных проб клиниколабораторных показателей, параметров ФВД, ПСВ, улучшению состояния больных.
...
27 06 2026 14:56:58
Статья в формате PDF
266 KB...
26 06 2026 7:34:47
Статья в формате PDF
152 KB...
25 06 2026 22:53:17
Статья в формате PDF
268 KB...
24 06 2026 12:26:29
Статья в формате PDF
263 KB...
23 06 2026 23:55:27
Статья в формате PDF
505 KB...
22 06 2026 9:43:44
Статья в формате PDF
83 KB...
20 06 2026 23:49:38
Статья в формате PDF
118 KB...
19 06 2026 18:53:50
Статья в формате PDF
115 KB...
17 06 2026 7:25:38
Статья в формате PDF
109 KB...
16 06 2026 18:41:18
Статья в формате PDF
263 KB...
13 06 2026 7:17:10
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
