ПРИМЕНЕНИЕ МЕТОДА ДЭВИСА ПРИ ОПРЕДЕЛЕНИИ КОНСТАНТ ДИССОЦИАЦИИ ДИЭЛЕКТРОЛИТОВ > Полезные советы
Тысяча полезных мелочей    

ПРИМЕНЕНИЕ МЕТОДА ДЭВИСА ПРИ ОПРЕДЕЛЕНИИ КОНСТАНТ ДИССОЦИАЦИИ ДИЭЛЕКТРОЛИТОВ

ПРИМЕНЕНИЕ МЕТОДА ДЭВИСА ПРИ ОПРЕДЕЛЕНИИ КОНСТАНТ ДИССОЦИАЦИИ ДИЭЛЕКТРОЛИТОВ

Танганов Б.Б. Ангапов В.Д. Багаева Т.В. Алексеева И.А. В работе обосновано применение метода Дэвиса для оценки коэффициентов активности ионов, образующихся в кислотно-основной системе, при определении термодинамических констант диссоциации ароматических кислот в среде диметилформамида. Статья в формате PDF 157 KB

Как было показано в работах [3,4,5,6], расчеты по ионным составляющим в процессах переноса [1,2] (теплопроводность, электрическая проводимость, вязкость и коэффициенты диффузии в растворах сильных и слабых электролитов) лишь на основании ионов, образующихся по первой ступени диссоциации многофункциональных соединений, не совсем объективны. Требуется учет равновесных концентраций всех ионов, находящихся в кислотно-основной системе. Наиболее полную информацию по концентрациям всех частиц можно получить из логарифмических диаграмм «lg C - lg a (SH+)», где lg C представляет концентрации всех ионов в растворе, а lg a (SH+) - активность сольватированного в любом растворителе протона (активность ионов лиония) [3,4,5,6].

При оценке коэффициентов активности наиболее приемлемым является уравнение Дэвиса [8]:

-lgfi = [A·Zi·I0.5/(1+I0.5)]-0.1·I,

так как метод Дебая требует введения а - расстояний наибольшего сближения частиц, которые, строго говоря, являются неопределенными и обычно принимаемыми не более 5·10-8см. Поскольку в растворе все частицы (даже нейтральные молекулы) находятся в сольватированном состоянии (молекулярные сольваты, сольватированные ионы, ассоциированные ионы и т.д.), то даже простая сумма радиусов сольватированных ионов (в первом приближении) не дает полной информации по расстояниям наименьшего сближения ионов и вряд ли будет постоянной для одних и тех же сольватированных катиона и аниона в любом растворителе и равной 5·10-8см.

Коэффициент А определяется соотношением

,

где NA - число Авогадро, kБ - постоянная Больцмана, ε - диэлектрическая проницаемость среды, Т - температура по Кельвину. Для ДМФ получена величина А = 1.6363.

Таким образом, уравнение Дэвиса устраняет неопределенность с расстоянием наибольшего сближения частиц и вполне приемлемо для расчетов коэффициентов активности ионов в водных, тем более в неводных, растворах, где в зависимости от природы растворителя одни и те же ионы хаpaктеризуются различными радиусами сольватированных оболочек. Расчеты термодинамических констант диссоциации электролитов дают более достоверные результаты [7] по сравнению с методом Дебая.

В качестве примера оценки ионных сил, применимости коэффициентов активности по Дэвису и определения термодинамических констант диссоциации ароматических двухосновных кислот в табл. 1 - 5 приведены необходимые данные, включающие некоторые фрагменты в буферных областях от 25 до 75% нейтрализации двухосновных дифеновой (табл. 1), дифенилфталиддикарбоновой (ДФФДК) (табл. 2), о-фталевой (табл. 3), изофталевой (табл. 4) и терефталевой (табл. 5) кислот гуанидином в ДМФА: потенциал электродной системы в зависимости от объема добавленного титранта, логарифмы концентраций всех равновесных частиц, образующихся при диссоциации дикислоты, полный учет которых дает возможность объективной оценки ионной силы, коэффициентов активности по Дэвису и соответствующих величин показателей термодинамических констант диссоциации, определяемых по ур. (1) и (2).

                               (1)

 ,                             (2)

Таблица 1. Данные для определения термодинамических констант диссоциации 4.215·10-3 М раствора дифеновой кислоты титрованием 5.0178·10-2 М раствором гуанидина в ДМФА

Vi

E, B

-lg a(SH+)

lg

[H2An]

lg

[HAn-]

lg

[An2-]

I 0,5

f1

f2

pK1

pK2

0.5

-0.130

9.217

-2.375

-3.058

-5.168

0.0212

0.9247

0.7309

9.93

11.43

0.9

-0.156

9.665

-2.375

-2.609

-4.719

0.0355

0.8788

0.5959

9.95

11.94

1.3

-0.190

10.252

-2.727

-2.375

-4.133

0.0475

0.8434

0.5052

9.97

12.23

1.7

-0.215

10.683

-3.158

-2.375

-3.702

0.0500

0.8361

0.4878

9.98

12.24

2.1

-0.239

11.096

-3.571

-2.375

-3.288

0.0560

0.8194

0.4499

9.98

12.27

2.5

-0.260

11.458

-3.933

-2.375

-2.926

0.0669

0.7903

0.3890

10.00

12.31

2.9

-0.280

11.803

-4.278

-2.375

-2.581

0.0857

0.7439

0.3047

10.03

12.39

3.3

-0.300

12.148

-4.623

-2.513

-2.375

0.0998

0.7119

0.2552

10.18

12.45

На рис. 1, 2, 3, 4, 5 нанесены упомянутые выше логарифмические диаграммы «lg C - lg a (SH+)», позволяющие оценить равновесные концентрации всех заряженных и незаряженных частиц (сольватированных нейтральных молекул и ионов), образующихся при диссоциации кислоты и при титровании ее сильным основанием.

Рис. 1. Логарифмическая диаграмма дифеновой кислоты в среде ДМФА ( ◊ - концентрация кислоты Н2Аn,  - иона HAn-, ∆ - иона An2-)

Рис. 2. Логарифмическая диаграмма ДФФДК в среде ДМФА ( ◊ - концентрация кислоты Н2Аn,  - иона HAn-, ∆ - иона An2-)

Рис. 3. Логарифмическая диаграмма о-фталевой кислоты в среде ДМФА (◊ - концентрация кислоты Н2Аn,  - иона HAn-, ∆ - иона An2-)

Рис. 4. Логарифмическая диаграмма изофталевой кислоты в среде ДМФА (◊ - концентрация кислоты Н2Аn,  - иона HAn-, ∆ - иона An2-)

 

Рис. 5. Логарифмическая диаграмма терефталевой кислоты в среде ДМФА (◊ - концентрация кислоты Н2Аn,  - иона HAn-, ∆ - иона An2-)

Таблица 2. Данные для определения ионной силы, коэффициентов активности и термодинамических констант диссоциации 3.193·10-3 М раствора ДФФДК титрованием 4.6956·10-2 М раствором гуанидина в ДМФА

Vi

E, B

-lg a(SH+)

lg

[H2An]

lg

[HAn-]

lg

[An2-]

I 0,5

 f1

f2

pK1

pK2

0.4

-0.123

9.096

-2.496

-3.089

-4.639

0.02128

0.9246

0.7305

9.72

10.75

0.8

-0.155

9.648

-2.496

-2.537

-4.087

0.04016

0.8649

0.5590

9.75

11.38

1.2

-0.180

10.079

-2.885

-2.496

-3.656

0.04513

0.8502

0.5218

9.76

11.45

1.6

-0.200

10.424

-3.230

-2.496

-3.312

0.05071

0.8342

0.4834

9.77

11.47

2.0

-0.220

10.769

-3.575

-2.496

-2.967

0.06127

0.8052

0.4192

9.78

11.52

2.4

-0.240

11.113

-3.919

-2.496

-2.622

0.07981

0.7580

0.3287

9.81

11.60

2.8

-0.260

11.458

-4.264

-2.714

-2.496

0.08573

0.7439

0.3047

10.03

11.63

Таблица 3. Данные для определения ионной силы, коэффициентов активности и термодинамических констант диссоциации 0.03718 н. раствора о-фталевой кислоты титрованием гуанидином в среде ДМФА

Vi

E, B

-lg

a(SH+)

lg[H2An]

lg

[HАn-]

lg[An2-]

I 0,5

f1

f2

pK1

pK2

0.4

0.055

6.0276

-1.7307

-2.2531

-6.6331

0.0528

0.8254

0.4632

6.63

10.65

0.8

0.040

6.2862

-1.7307

-1.9945

-6.3745

0.0711

0.8003

0.4090

6.66

10.99

1.2

0.036

6.3552

-1.7307

-1.9255

-6.3055

0.0770

0.7831

0.3749

6.66

11.08

1.8

0.023

6.5793

-1.7307

-1.7307

-6.0814

0.0964

0.7534

0.3208

6.72

11.36

2.2

0.020

6.6310

-1.8117

-1.7307

-6.0296

0.0964

0.7334

0.2877

6.69

11.36

2.7

0.011

6.7862

-1.9669

-1.7307

-5.8745

0.0964

0.7333

0.2875

6.69

11.36

3.1

-0.100

8.7000

-3.8807

-1.7307

-3.9607

0.0975

0.7331

0.2873

6.69

11.36

3.5

-0.178

10.045

-5.2255

-1.7307

-2.6159

0.1189

0.7326

0.2864

6.72

11.45

3.9

-0.200

10.424

-5.6048

-1.7307

-2.2365

0.1445

0.6889

0.2233

6.75

11.55

4.4

-0.225

10.855

-6.0359

-1.7307

-1.8055

0.2014

0.5813

0.1119

6.82

11.75

4.8

-0.245

11.200

-6.3807

-2.0007

-1.7307

0.2053

0.5617

0.0972

7.09

11.76

5.0

-0.255

11.372

-6.5531

-2.1731

-1.7307

0.2013

0.5576

0.0944

7.26

11.75

Таблица 4. Данные для определения ионной силы, коэффициентов активности и термодинамических констант диссоциации 0.01687 н. раствора изофталевой кислоты титрованием гуанидином в среде ДМФА

Vi

E, B

-lg a(SH+)

lg

[H2An]

lg

[HAn-]

lg

[An2-]

I 0,5

 f1

f2

pK1

pK2

0.2

-0.140

9.4111

-2.0740

-2.1829

-2.5629

0.0935

0.7259

0.2760

9.66

10.21

0.6

-0.145

9.4989

-2.0740

-2.0950

-2.4750

0.1035

0.7040

0.2438

9.67

10.33

1.0

-0.149

9.5692

-2.1232

-2.0740

-2.4048

0.1099

0.6904

0.2253

9.68

10.38

1.4

-0.153

9.6395

-2.1935

-2.0740

-2.3345

0.1161

0.6779

0.2092

9.69

10.41

1.8

-0.157

9.7098

-2.2638

-2.0740

-2.2642

0.1229

0.6644

0.1928

9.69

10.43

2.4

-0.175

10.0260

-2.5800

-2.2001

-2.0740

0.1415

0.6297

0.1551

9.84

10.50

Таблица 5. Данные для определения ионной силы, коэффициентов активности и термодинамических констант диссоциации 0.03250 н. раствора терефталевой кислоты титрованием гуанидином/ДМФА

Vi

E, B

-lg a(SH+)

lg

[H2An]

lg

[HAn-]

lg

[An2-]

I 0,5

f1

f2

pK1

pK2

0.5

-0.048

7.8034

-1.789

-2.168

-5.375

0.0583

0.8132

0.4362

8.27

11.28

0.9

-0.060

8.0103

-1.789

-1.962

-5.168

0.0740

0.7723

0.3545

8.29

11.55

1.3

-0.070

8.1827

-1.789

-1.789

-4.996

0.0902

0.7334

0.2877

8.31

11.79

1.7

-0.079

8.3379

-1.944

-1.789

-4.841

0.0903

0.7333

0.2875

8.31

11.79

2.1

-0.090

8.5276

-2.133

-1.789

-4.651

0.0904

0.7331

0.2872

8.31

11.79

2.5

-0.125

9.1310

-2.737

-1.789

-4.048

0.0911

0.7314

0.2845

8.32

11.80

2.9

-0.240

11.1138

-4.720

-1.789

-2.065

0.1591

0.5995

0.1270

8.40

12.06

3.3

-0.251

11.3034

-4.909

-1.789

-1.875

0.1864

0.5576

0.0944

8.43

12.16

3.5

-0.253

11.3379

-4.944

-1.789

-1.841

0.1922

0.5493

0.0887

8.44

12.18

3.7

-0.255

11.3724

-4.978

-1.789

-1.806

0.1983

0.5408

0.0833

8.45

12.20

3.9

-0.257

11.4067

-5.013

-1.806

-1.789

0.2008

0.5375

0.0812

8.46

12.21

4.1

-0.261

11.4759

-5.082

-1.875

-1.789

0.1979

0.5414

0.0836

8.53

12.20

4.3

-0.265

11.5448

-5.151

-1.944

-1.789

0.1954

0.5448

0.0858

8.60

12.19

Таблица 6. Статистическая обработка определенных величин показателей термодинамических констант диссоциации дикарбоновых ароматических кислот в среде ДМФА

№

Кислота

Число точек

Доверительный

интервал

1.

Дифеновая

30

рК1 = 10.03 ± 0.40; рК2 = 12.22 ± 0.78

2.

Дифенилфталид-дикарбоновая

27

рК1 = 9.82 ± 0.45; рК2 = 11.44 ± 0.69

3.

о - Фталевая

30

рК1 = 6.947 ± 0.315; рК2 = 11.220 ± 0.566

4.

Изофталевая

25

рК1 = 9.791 ± 0.140; рК2 = 10.327 ± 0.191

5.

Терефталевая

41

рК1 = 8.458 ± 0.193; рК2 = 11.697 ± 0.505

Статистическая обработка экспериментально определенных термодинамических констант диссоциации ароматических дикарбоновых кислот в среде ДМФА приводит к доверительным интервалам, внутри которых с вероятностью 0.95 находятся экспериментальные величины рК1 и рК2 (табл.6).

Таким образом, обоснована применимость уравнения Дэвиса, свободного от неопределенности расстояний наибольшего сближения ионов по Дебаю-Хюккелю, к концепции теоретической оценки коэффициентов активности и экспериментального определения термодинамических констант диссоциации ароматических кислот в среде органических растворителей при раздельной и совместной нейтрализации обеих кислотных групп.

СПИСОК ЛИТЕРАТУРЫ:

  1. Балданов М.М., Балданова Д.М. Жигжитова С.Б., Танганов Б.Б. // ДАН ВШ России. -2006. -№ 1. -С.25.
  2. Дашиев Р.З., Балданов М.М., Танганов Б.Б.//ДАН ВШ России.-2005.-.№1.-С.12
  3. Танганов Б.Б., Алексеева И.А.//Вестник ВСГТУ.-2005.-Вып.2.-С.5; -Вып.3.-С.5.
  4. Танганов Б.Б., Алексеева И.А. // ЖОХ.-2005.-Т.75.-Вып.11.-С.1775.
  5. Танганов Б.Б., Алексеева И.А. // ЖОХ.-2006.-Т.76.-Вып.11.-С.1800.
  6. Танганов Б.Б., Алексеева И.А. // Вестник БГУ.-Серия «Химия».-2006.-С.70.
  7. Танганов Б.Б. // ЖОХ.-2007.-Т.77.-Вып.8.-С.1238.
  8. Davies C.W. // J. Chem.Soc. - 1938. -P.2093.


КИСЛОТНО-ЩЕЛОЧНОЙ БАЛАНС У ЖИВОТНЫХ НА РАННИХ ЭТАПАХ ОНТОГЕНЕЗА

КИСЛОТНО-ЩЕЛОЧНОЙ БАЛАНС У ЖИВОТНЫХ НА РАННИХ ЭТАПАХ ОНТОГЕНЕЗА Статья в формате PDF 111 KB...

24 04 2024 6:21:58

РАЦИОНАЛЬНОЕ НЕДРОПОЛЬЗОВАНИЕ – ПУТЬ К ПРОЦВЕТАНИЮ

РАЦИОНАЛЬНОЕ НЕДРОПОЛЬЗОВАНИЕ – ПУТЬ К ПРОЦВЕТАНИЮ Статья в формате PDF 213 KB...

23 04 2024 13:18:20

О РАЗРАБОТКЕ НОВОГО ПРОФИЛЯ ПОДГОТОВКИ БАКАЛАВРОВ ХУДОЖЕСТВЕННОГО ОБРАЗОВАНИЯ

О РАЗРАБОТКЕ НОВОГО ПРОФИЛЯ ПОДГОТОВКИ БАКАЛАВРОВ ХУДОЖЕСТВЕННОГО ОБРАЗОВАНИЯ Статья в формате PDF 130 KB...

22 04 2024 23:21:32

ПРОФЕССИОНАЛЬНОЕ САМООПРЕДЕЛЕНИЕ ВЫПУСКНИКОВ ПЕДАГОГИЧЕСКОГО УНИВЕРСИТЕТА

ПРОФЕССИОНАЛЬНОЕ САМООПРЕДЕЛЕНИЕ ВЫПУСКНИКОВ ПЕДАГОГИЧЕСКОГО УНИВЕРСИТЕТА Статья в формате PDF 107 KB...

21 04 2024 14:58:35

ДИАГНОСТИРОВАНИЕ СТАНОЧНОГО ОБОРУДОВАНИЯ КАК ПРОЦЕСС ПОЛУЧЕНИЯ ИНФОРМАЦИИ

ДИАГНОСТИРОВАНИЕ СТАНОЧНОГО ОБОРУДОВАНИЯ КАК ПРОЦЕСС ПОЛУЧЕНИЯ ИНФОРМАЦИИ Статья в формате PDF 253 KB...

20 04 2024 4:52:53

РЕГЕНЕРАЦИЯ ЭПИДЕРМИСА И ОМОЛОЖЕНИЕ КОЖИ ЧЕЛОВЕКА

РЕГЕНЕРАЦИЯ ЭПИДЕРМИСА И ОМОЛОЖЕНИЕ КОЖИ ЧЕЛОВЕКА Статья в формате PDF 127 KB...

19 04 2024 21:57:14

Радикалпродуцирующая способность нейтрофилов и соотношение субпопуляций т-лимфоцитов у больных псориатической артропатией и эритродермией

Радикалпродуцирующая способность нейтрофилов и соотношение субпопуляций т-лимфоцитов у больных псориатической артропатией и эритродермией Статья в формате PDF 119 KB...

18 04 2024 15:49:49

ЭФФЕКТИВНОСТЬ ЦИКЛОФЕРОНА ПРИ НС-ВИРУСНОЙ ИНФЕКЦИИ У НАРКОЗАВИСИМЫХ ПОДРОСТКОВ

ЭФФЕКТИВНОСТЬ ЦИКЛОФЕРОНА ПРИ НС-ВИРУСНОЙ ИНФЕКЦИИ У НАРКОЗАВИСИМЫХ ПОДРОСТКОВ Статья в формате PDF 99 KB...

17 04 2024 21:52:15

НОВИНКА НА РЫНКЕ КОНСЕРВИРОВАННЫХ ВТОРЫХ БЛЮД

НОВИНКА НА РЫНКЕ КОНСЕРВИРОВАННЫХ ВТОРЫХ БЛЮД Статья в формате PDF 244 KB...

16 04 2024 17:32:16

КОМПЛЕКСНЫЙ АНАЛИЗ РЕГИОНАЛЬНОГО РИТЕЙЛА КАК ОСНОВА ФОРМИРОВАНИЯ ТОРГОВО-ЛОГИСТИЧЕСКОЙ СИСТЕМЫ РЕГИОНА

КОМПЛЕКСНЫЙ АНАЛИЗ РЕГИОНАЛЬНОГО РИТЕЙЛА КАК ОСНОВА ФОРМИРОВАНИЯ ТОРГОВО-ЛОГИСТИЧЕСКОЙ СИСТЕМЫ РЕГИОНА Статья в формате PDF 264 KB...

15 04 2024 6:46:39

СРАВНИТЕЛЬНАЯ КЛИНИКО-ЭПИДЕМИОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА БОЛЬНЫХ НЕСПЕЦИФИЧЕСКИМ ЯЗВЕННЫМ КОЛИТОМ И БОЛЕЗНЬЮ КРОНА, НАХОДИВШИХСЯ НА ЛЕЧЕНИИ В 1РКБ В 2009 Г.

СРАВНИТЕЛЬНАЯ КЛИНИКО-ЭПИДЕМИОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА БОЛЬНЫХ НЕСПЕЦИФИЧЕСКИМ ЯЗВЕННЫМ КОЛИТОМ И БОЛЕЗНЬЮ КРОНА, НАХОДИВШИХСЯ НА ЛЕЧЕНИИ В 1РКБ В 2009 Г. Статья в формате PDF 250 KB...

14 04 2024 8:57:11

ИССЛЕДОВАНИЕ УСЛОВИЙ ВЫДЕЛЕНИЯ И ОЧИСТКИ ГЛЮКОАМИЛАЗЫ ИЗ SACCHAROMYCES CEREVISIAE ЛВ-7

ИССЛЕДОВАНИЕ УСЛОВИЙ ВЫДЕЛЕНИЯ И ОЧИСТКИ ГЛЮКОАМИЛАЗЫ ИЗ SACCHAROMYCES CEREVISIAE ЛВ-7 Разработана методика выделения и очистки глюкоамилазы, включающая стадии ультрафильтрации на мембране УФМ-50, осаждения изопропиловым спиртом и гель-хроматографии на сефадексах G-25 и G-150, которая позволила получить гомогенный препарат глюкоамилазы из Saccharomyces cerevisiae ЛВ-7 с 70-кратной степенью чистоты; кажущаяся молекулярная масса фермента 99,8 кДа. ...

13 04 2024 1:52:36

ПЕРСПЕКТИВА ПРИМЕНЕНИЯ ФТОРИДА АММОНИЯ ДЛЯ ВЫДЕЛЕНИЯ СИНТЕТИЧЕСКИХ КАУЧУКОВ ИЗ ЛАТЕКСОВ

ПЕРСПЕКТИВА ПРИМЕНЕНИЯ ФТОРИДА АММОНИЯ ДЛЯ ВЫДЕЛЕНИЯ СИНТЕТИЧЕСКИХ КАУЧУКОВ ИЗ ЛАТЕКСОВ Изучена коагулирующая способность фторида аммония при выделении каучука из латекса СКС- 30АРК. Исследовано влияние температуры и концентрации раствора фторида аммония на полноту коагуляции. Проведена оценка свойств резиновых смесей и вулканизатов на основе каучука СКС-30 АРК, выделенного из латекса фторидом аммония. ...

12 04 2024 6:33:39

ПЕРСПЕКТИВЫ РАЗВИТИЯ ВУЗОВСКОЙ НАУКИ В ЕСТЕСТВОЗНАНИИ, БИОЛОГИИ, МЕДИЦИНЕ

ПЕРСПЕКТИВЫ РАЗВИТИЯ ВУЗОВСКОЙ НАУКИ В ЕСТЕСТВОЗНАНИИ, БИОЛОГИИ, МЕДИЦИНЕ Статья в формате PDF 173 KB...

11 04 2024 1:43:47

СОВРЕМЕННЫЕ ТЕНДЕНЦИИ РЕГИОНАЛЬНОЙ ИНТЕГРАЦИИ: ПРОБЛЕМЫ И ПРЕИМУЩЕСТВА

СОВРЕМЕННЫЕ ТЕНДЕНЦИИ РЕГИОНАЛЬНОЙ ИНТЕГРАЦИИ: ПРОБЛЕМЫ И ПРЕИМУЩЕСТВА Статья в формате PDF 308 KB...

10 04 2024 13:40:27

ПРОБЛЕМА УГЛЕКИСЛОТЫ

ПРОБЛЕМА УГЛЕКИСЛОТЫ Статья в формате PDF 93 KB...

09 04 2024 18:53:15

ПРОЕКТИРОВАНИЕ ФУНКЦИОНАЛЬНОЙ ПОДСИСТЕМЫ УЧЁТА ТОВАРНО-МАТЕРИАЛЬНЫХ ЦЕННОСТЕЙ В ЗАО «ТЕКЛАЙН»

ПРОЕКТИРОВАНИЕ ФУНКЦИОНАЛЬНОЙ ПОДСИСТЕМЫ УЧЁТА ТОВАРНО-МАТЕРИАЛЬНЫХ ЦЕННОСТЕЙ В ЗАО «ТЕКЛАЙН» Статья в формате PDF 364 KB...

08 04 2024 8:35:25

О НОВЫХ ПОДХОДАХ В ВУЗОВСКОМ ХУДОЖЕСТВЕННОМ ОБРАЗОВАНИИ

О НОВЫХ ПОДХОДАХ В ВУЗОВСКОМ ХУДОЖЕСТВЕННОМ ОБРАЗОВАНИИ Статья в формате PDF 128 KB...

07 04 2024 13:27:39

Денситометрия у женщин после овариоэктомии, осложненной компрессионными переломами позвоночника

Денситометрия у женщин после овариоэктомии, осложненной компрессионными переломами позвоночника Статья в формате PDF 102 KB...

06 04 2024 19:45:48

ИЗМЕНЕНИЕ ФИЗИКО-ХИМИЧЕСКИХ СВОЙСТВ РОТОВОЙ ЖИДКОСТИ У БОЛЬНЫХ ГИПЕРТОНИЧЕСКОЙ БОЛЕЗНЬЮ

ИЗМЕНЕНИЕ ФИЗИКО-ХИМИЧЕСКИХ СВОЙСТВ РОТОВОЙ ЖИДКОСТИ У БОЛЬНЫХ ГИПЕРТОНИЧЕСКОЙ БОЛЕЗНЬЮ Статья в формате PDF 85 KB...

05 04 2024 14:43:28

ЗЫБАЛОВ ВЛАДИМИР СТЕПАНОВИЧ

ЗЫБАЛОВ ВЛАДИМИР СТЕПАНОВИЧ Статья в формате PDF 230 KB...

04 04 2024 16:49:20

ДИЕТИЧЕСКИЕ ПРОДУКТЫ ПИТАНИЯ – ОСНОВА ЗДОРОВЬЯ

ДИЕТИЧЕСКИЕ ПРОДУКТЫ ПИТАНИЯ – ОСНОВА ЗДОРОВЬЯ Статья в формате PDF 284 KB...

03 04 2024 19:27:52

СТРУКТУРНЫЕ ОСОБЕННОСТИ И ГЕМОДИНАМИЧЕСКАЯ РОЛЬ ПОЛИПОВИДНЫХ ПОДУШЕК АРТЕРИАЛЬНОГО РУСЛА

СТРУКТУРНЫЕ ОСОБЕННОСТИ И ГЕМОДИНАМИЧЕСКАЯ РОЛЬ ПОЛИПОВИДНЫХ ПОДУШЕК АРТЕРИАЛЬНОГО РУСЛА Статья в формате PDF 114 KB...

02 04 2024 9:37:52

ДИФФЕРЕНЦИАЛЬНЫЙ ДИАГНОЗ ХРОНИЧЕСКОГО БРОНХИТА У ДЕТЕЙ И ПОДРОСТКОВ

ДИФФЕРЕНЦИАЛЬНЫЙ ДИАГНОЗ ХРОНИЧЕСКОГО БРОНХИТА У ДЕТЕЙ И ПОДРОСТКОВ Статья в формате PDF 233 KB...

01 04 2024 10:38:13

ИССЛЕДОВАНИЕ ВОПРОСОВ ЭФФЕКТИВНОСТИ ПРОТИВОПОЖАРНЫХ МЕРОПРИЯТИЙ

ИССЛЕДОВАНИЕ ВОПРОСОВ ЭФФЕКТИВНОСТИ ПРОТИВОПОЖАРНЫХ МЕРОПРИЯТИЙ Статья в формате PDF 262 KB...

31 03 2024 12:14:17

Шестой этап обращения куфического дирхема на Верхневолжском (Волго-Клязьминском) денежном рынке (825-849 гг.); значение фрагментированных монет; драхмы и полудрахмысасанидского типа

Шестой этап обращения куфического дирхема на Верхневолжском (Волго-Клязьминском) денежном рынке (825-849 гг.); значение фрагментированных монет; драхмы и полудрахмысасанидского типа Статья в формате PDF 263 KB...

30 03 2024 3:36:40

ВЛИЯНИЕ ПРЕРЫВИСТОЙ ГИПОБАРИЧЕСКОЙ ГИПОКСИИ НА МИКРОГЕМОЦЕРКУЛЯТОРНОЕ РУСЛО ЩИТОВИДНОЙ ЖЕЛЕЗЫ

ВЛИЯНИЕ ПРЕРЫВИСТОЙ ГИПОБАРИЧЕСКОЙ ГИПОКСИИ НА МИКРОГЕМОЦЕРКУЛЯТОРНОЕ РУСЛО ЩИТОВИДНОЙ ЖЕЛЕЗЫ Статья в формате PDF 127 KB...

29 03 2024 13:36:46

CHYTRIDIOMYCOSIS У ЛИЧИНОК RANA ARVALIS NILSSON НА СРЕДНЕМ УРАЛЕ

CHYTRIDIOMYCOSIS У ЛИЧИНОК RANA ARVALIS NILSSON НА СРЕДНЕМ УРАЛЕ На основании диагностических признаков приводятся доказательства, указывающие на то, что Chytridiomycosis существует в популяциях Rana arvalis на Среднем Урале. Показана методика обнаружения заболевания по аномалиям ротового аппарата личинок и отслеживания динамики частоты встречаемости его в популяции. В экстремальных условиях инфекция поражает ослабленных и ведет к их выбpaковке, что приводит к ускорению адаптации популяции в целом в быстро изменяемой среде. ...

28 03 2024 9:54:38

Совершенствование технологии производства биологически активных обезжиренных фосфолипидов

Совершенствование технологии производства биологически активных обезжиренных фосфолипидов Статья в формате PDF 115 KB...

27 03 2024 16:46:13

КЛИНИЧЕСКОЕ ЗНАЧЕНИЕ ИММУНОЛОГИЧЕСКОЙ КОНЦЕПЦИИ СЕПСИСА

КЛИНИЧЕСКОЕ ЗНАЧЕНИЕ ИММУНОЛОГИЧЕСКОЙ КОНЦЕПЦИИ СЕПСИСА Статья в формате PDF 135 KB...

26 03 2024 16:52:37

МИКРОТОПОГРАФИЯ ПОВЕРХНОСТИ ПОСЛЕ ВЫГЛАЖИВАНИЯ

МИКРОТОПОГРАФИЯ ПОВЕРХНОСТИ ПОСЛЕ ВЫГЛАЖИВАНИЯ Статья в формате PDF 265 KB...

25 03 2024 8:36:39

О РЕДКИХ ВИДАХ ЛИШАЙНИКОВ РЕСПУБЛИКИ ТАТАРСТАН

О РЕДКИХ ВИДАХ ЛИШАЙНИКОВ РЕСПУБЛИКИ ТАТАРСТАН Проведена инвентаризация лихенофлоры Республики Татарстан (РТ). Показана роль особо охраняемых природных территорий в сохранении флористического разнообразия. Дан спектр семейств редких видов во флоре обследованной территории и анализ состава географических элементов. Рассмотрено распределение редких видов по основным типам местообитаний. Даются некоторые сведения о редких и исчезающих лишайниках для включения в Красную книгу РТ. ...

24 03 2024 0:13:22

Реакция коркового вещества надпочечников на острое и длительное введение бактериального эндотоксина липополисахарида у крыс (морфо-функциональное исследование)

Реакция коркового вещества надпочечников на острое и длительное введение бактериального эндотоксина липополисахарида у крыс (морфо-функциональное исследование) Статья в формате PDF 115 KB...

23 03 2024 1:19:34

МОРФОГЕНЕТИЧЕСКАЯ РОЛЬ СЕТИ В ФИЗИОЛОГИИ И ПАТОЛОГИИ ЯИЧНИКОВ

МОРФОГЕНЕТИЧЕСКАЯ РОЛЬ СЕТИ В ФИЗИОЛОГИИ И ПАТОЛОГИИ ЯИЧНИКОВ Статья в формате PDF 90 KB...

22 03 2024 16:48:32

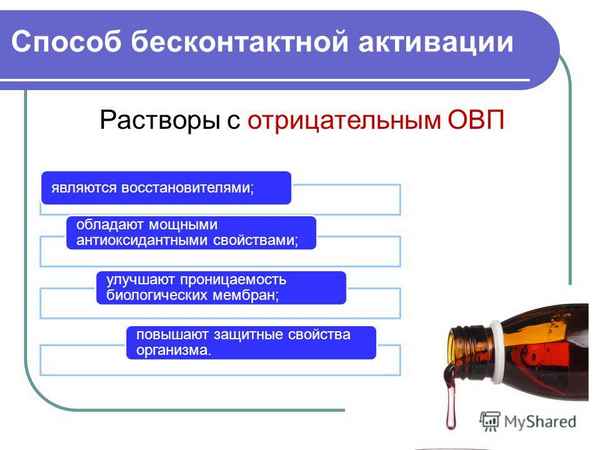НЕОБЫЧНЫЕ СВОЙСТВА НЕКОТОРЫХ БЕСКОНТАКТНО АКТИВИРОВАННЫХ РАСТВОРОВ

НЕОБЫЧНЫЕ СВОЙСТВА НЕКОТОРЫХ БЕСКОНТАКТНО АКТИВИРОВАННЫХ РАСТВОРОВ Исследованы водные растворы неорганических соединений бесконтактно активированные в бездиафрагменном электролизере. Активация в большинстве случаев сопровождается уменьшением окислительно-восстановительного потенциала растворов. Показано, что релаксация бесконтактно активированных растворов начинается спустя 30-40 минут по завершении активации и протекает в колебательном режиме. Растворы бихромата калия при активации приобретают отрицательный окислительно-восстановительный потенциал, спектр поглощения растворов при этом не изменяется. Для растворов перманганата калия наблюдается противоположный эффект. Изменения окислительно-восстановительного потенциала невелики, однако изменение спектра поглощения раствора свидетельствует об образовании продукта, не имеющем аналогов при химическом восстановлении KMnO4. ...

21 03 2024 16:46:17

ФАКТОРЫ, ВЛИЯЮЩИЕ НА РЕПРОДУКТИВНОЕ ЗДОРОВЬЕ ДЕТЕЙ

ФАКТОРЫ, ВЛИЯЮЩИЕ НА РЕПРОДУКТИВНОЕ ЗДОРОВЬЕ ДЕТЕЙ Статья в формате PDF 123 KB...

20 03 2024 16:34:26

ЗАКОНОМЕРНОСТИ ИЗМЕНЕНИЙ ГОРМОНАЛЬНОГО БАЛАНСА В ДИНАМИКЕ ОПУХОЛЕВОЙ ПРОГРЕССИИ У БОЛЬНЫХ РАКОМ МОЛОЧНОЙ ЖЕЛЕЗЫ

ЗАКОНОМЕРНОСТИ ИЗМЕНЕНИЙ ГОРМОНАЛЬНОГО БАЛАНСА В ДИНАМИКЕ ОПУХОЛЕВОЙ ПРОГРЕССИИ У БОЛЬНЫХ РАКОМ МОЛОЧНОЙ ЖЕЛЕЗЫ Исследование гормонального баланса в группах пациенток с I-IIA и IIB-IIIA стадиями распространения paка молочной железы позволило обнаружить прогрессирующее снижение содержания в крови прогестерона, коррелирующее со стадией распространения опухолевого процесса. Уровень эстриола снижался в равной мере в обеих группах наблюдения пациентов (I-IIA и IIB-IIIA стадиями распространения неоплазии) по сравнению с показателями контроля. Указанные сдвиги гормонального баланса наблюдались в разных возрастных группах от 29 до 49 лет, достигая максимальных сдвигов в пре- и менопаузальный периоды. Содержание эстрадиола в крови оставалось в пределах нормы при I-IIA стадиях развития заболевания, резко возрастая при метастатической форме paка молочной железы. Мониторинг показателей содержания в крови прогестерона и эстрадиола может быть использован как один из способов оценки эффективности комплексной терапии заболевания и степени распространения неоплазии при paке молочной железы. ...

19 03 2024 11:36:43

МЕТОД ГРАНИЧНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ В ОЦЕНКЕ СОБСТВЕННЫХ ЧАСТОТ ОБЛАСТИ СО СКОСАМИ СТЕН

МЕТОД ГРАНИЧНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ В ОЦЕНКЕ СОБСТВЕННЫХ ЧАСТОТ ОБЛАСТИ СО СКОСАМИ СТЕН Статья в формате PDF 835 KB...

18 03 2024 23:48:17

ВЛИЯНИЕ АНТРОПОГЕННОГО ВОЗДЕЙСТВИЯ НА РАСТИТЕЛЬНОСТЬ МАРШРУТА №1 ПРИРОДНОГО ПАРКА «ЛЕНСКИЕ СТОЛБЫ»

ВЛИЯНИЕ АНТРОПОГЕННОГО ВОЗДЕЙСТВИЯ НА РАСТИТЕЛЬНОСТЬ МАРШРУТА №1 ПРИРОДНОГО ПАРКА «ЛЕНСКИЕ СТОЛБЫ» Статья в формате PDF 251 KB...

17 03 2024 10:14:43

К ВОПРОСУ О СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИХ ОСОБЕННОСТЯХ ДЕТЕЙ, ИМЕЮЩИХ ХРОНИЧЕСКИЕ ЗАБОЛЕВАНИЯ

К ВОПРОСУ О СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИХ ОСОБЕННОСТЯХ ДЕТЕЙ, ИМЕЮЩИХ ХРОНИЧЕСКИЕ ЗАБОЛЕВАНИЯ Статья в формате PDF 196 KB...

16 03 2024 21:35:28

Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::