ХАРАКТЕРНЫЕ ОБЛАСТИ ПОДВИЖНОЙ ПЛОСКОСТИ
В задачах на плоское движение твердого тела известны траектория полюса и угол поворота плоскости в функции от пути полюса. Используются понятия мгновенных центров скоростей (МЦС) и ускорений (МЦУ), круги Лагира (круг поворота, или круг перегибов) и Брессе (круг перемены), имеющие геометрические признаки, не включающие в себя параметра времени. Рассмотрим эти особенности.
Введем обозначения
где
где vA и - скорость и касательное ускорение полюса А.
Положим, .
Эти выражения определяют единственную точку Q (рисунок), в которой одновременно выполняется два условия: из первого следует, что ее траектория имеет перегиб (нормальное ускорение точки равно нулю), второе свидетельствует о том, что при выполнении условия G = K (ее касательное ускорение равно нулю).
Точку Q назовем мгновенным центром производных перемещений (МЦПП). При она является мгновенным центром ускорений (МЦУ).
Ее координаты находятся совместным решением уравнений
откуда
Координаты точки Q в подвижной системе отсчета uO′v находятся по формулам перехода
Угол α:
Выделим следующие области подвижной плоскости.
Область А. Траектории точек этой области в направлении прямых, соединяющих эти точки с мгновенным центром перемещений (мгновенных радиусов), имеют экстремумы, и обращены выпуклостью к точке Р. Радиусы кривизны их траекторий отрицательны (ρ < 0). При этом точки имеют свой знак разности (Г - К). Положим, Г > К.
Область В. Траектории точек в направлении мгновенных радиусов обращены вогнутостью к точке Р. Радиусы их кривизны положительны (ρ > 0), при этом Г < К.
Область С. Траектории точек в направлении мгновенных радиусов обращены выпуклостью к точке Р. Радиусы их кривизны отрицательны (ρ < 0), при этом Г < К.
Область D. Траектории точек в направлении мгновенных радиусов обращены вогнутостью к точке Р. Радиусы их кривизны положительны (ρ > 0) , при этом Г > К.
Хаpaктеристики областей приведены в таблице.
Рассмотрен пример
|
Области и их границы |
ρ |
Г - К |
|
А |
<0 |
>0 |
|
А - С |
<0 |
0 |
|
С |
<0 |
<0 |
|
С - В |
∞ |
<0 |
|
В |
>0 |
<0 |
|
В - D |
>0 |
0 |
|
D |
>0 |
>0 |
|
А - D |
∞ |
>0 |
|
Точка Q |
∞ |
=0 |
Заданы: траектория точки А
закон изменения угла координаты точки А: uA = 4 см; vA = 6 см (uB = 0 см; vB = -36 см).
Построены траектории точек А и В для положения подвижной плоскости, соответствующего положению точки А (30; 8,24) построены круг Лагира. Круг Брессе построен для двух вариантов:
1. При
2. При
Показано, что круг Брессе по отношению к нормали n-n располагается с той или с другой ее стороны в зависимости от знака В (B > 0 или B < 0).
Рассмотренные понятия мгновенного центра производных перемещений и хаpaктерных областей подвижной плоскости наглядно отражают геометрические признаки плоского движения твердого тела.
Статья в формате PDF
285 KB...
18 04 2024 20:10:10
Статья в формате PDF
125 KB...
17 04 2024 23:56:16
Статья в формате PDF
307 KB...
16 04 2024 0:58:19
Статья в формате PDF
151 KB...
15 04 2024 17:25:25
Статья в формате PDF
245 KB...
14 04 2024 5:48:18
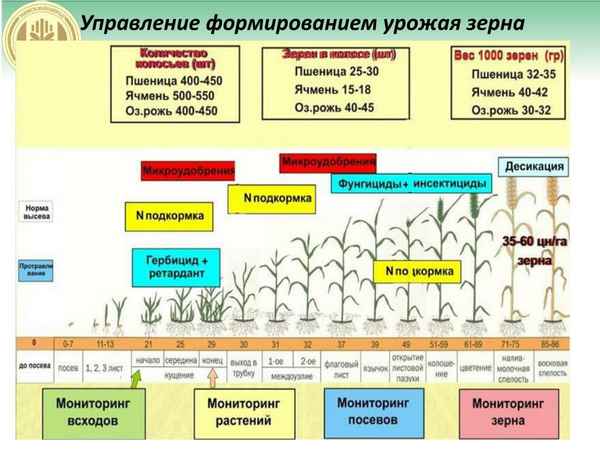Установлено, что применение биопрепаратов биогумус, гуми и альбит при замачивании семян и некорневой подкормке раннеспелых гибридов огурца в пленочной теплице, положительно влияют на энергию прорастания и всхожесть семян, ускоряют рост и развитие растений огурца, сокращают межфазный период на 3- 4 дня, вегетационный период, на 5-6 дней. Благоприятно влияют на водный режим растений, увеличение ассимиляционной поверхности, фотосинтетический потенциал и урожайность. Наиболее эффективное действие оказывали биопрепараты биогумус и гумми на гибридах, отечественной селекции Арина и голландской Машенька.
...
13 04 2024 4:23:52
Статья в формате PDF
262 KB...
12 04 2024 21:45:29
Статья в формате PDF
120 KB...
11 04 2024 15:37:35
Статья в формате PDF
139 KB...
10 04 2024 11:29:38
Статья в формате PDF
140 KB...
09 04 2024 8:22:35
Статья в формате PDF
111 KB...
08 04 2024 11:56:33
В статье рассматриваются основные начальные этапы научного изучения природных условий и фауны млекопитающих Кавказа. Рассмотрен вклад выдающихся научных деятелей России в становление и развитие отечественной териологии на Кавказе, приводятся интересные сведения об отдельных биографических моментах ученых, связанных с освоением изучаемой территории.
...
07 04 2024 5:48:48
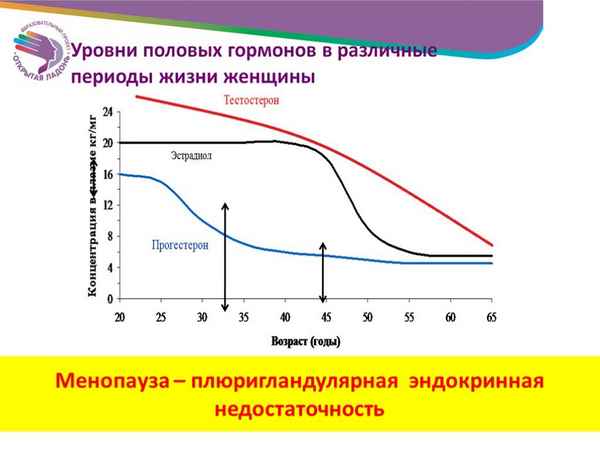
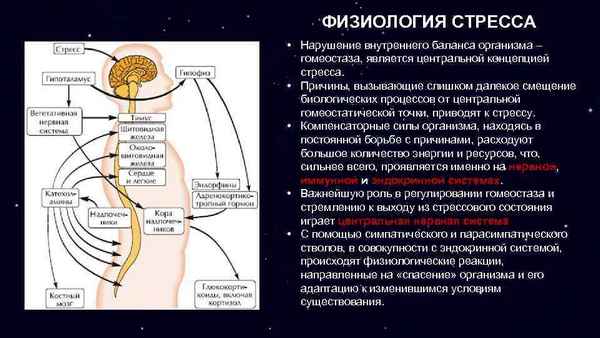Проведен анализ эффективности курсового гетеросуггестивного воздействия на функциональное состояние ЦНС у женщин репродуктивного возраста. С помощью методов электроэнцефалографии и спектрального анализа вариабельности сердечного ритма получены достоверные данные о положительной динамике на центральном и вегетативном уровнях обеспечения психофизиологической устойчивости обследованных женщин.
...
06 04 2024 14:51:45
Статья в формате PDF
111 KB...
05 04 2024 9:19:41
Статья в формате PDF
100 KB...
04 04 2024 1:39:34
Статья в формате PDF
127 KB...
03 04 2024 11:43:13
Статья в формате PDF
99 KB...
02 04 2024 11:27:16
Статья в формате PDF
146 KB...
31 03 2024 13:26:25
Статья в формате PDF
250 KB...
30 03 2024 7:24:28
Статья в формате PDF 242 KB...
29 03 2024 23:40:35
Статья в формате PDF
126 KB...
28 03 2024 21:46:33
Статья в формате PDF
316 KB...
27 03 2024 15:57:51
Статья в формате PDF
131 KB...
25 03 2024 23:56:39
Анализ опыта по восстановлению методом агростепей растительности на нарушенных кормовых угодьях долины средней Лены показал, что метод при соблюдении экологических условий и видового состава участков обеспечивает восстановление растительности, проявляющееся в повышении проективного покрытия и доминировании в травостое целинных видов. Соответствие экологических условий и видового состава травостоя при подборе участков обеспечивает восстановление растительности нарушенных участков до 70–75 % и доминирование в травостое целинных видов до 60–65 % в условиях нормального и сильного засоления.
...
24 03 2024 23:29:29
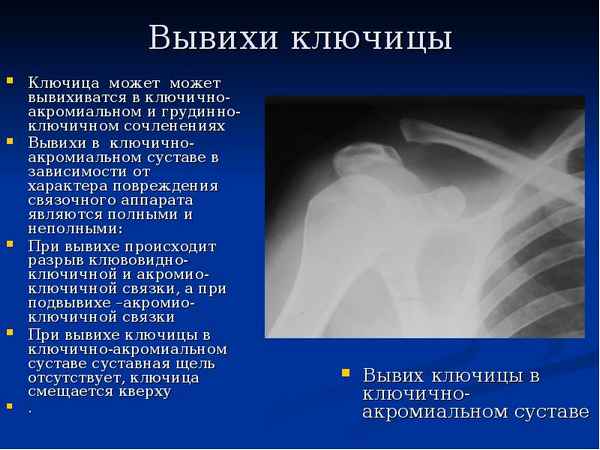Изучена анатомическая изменчивость строения акромиально-ключичного сустава и прочность его связок. Разработан собственный способ лечения больных с вывихом акромиального конца ключицы. Приведены показания для консервативного и хирургического лечения вывихов ключицы.
...
23 03 2024 6:42:31
Статья в формате PDF
109 KB...
21 03 2024 22:43:34
Статья в формате PDF
173 KB...
20 03 2024 23:23:49
Статья в формате PDF
106 KB...
19 03 2024 14:59:28
Статья в формате PDF
115 KB...
18 03 2024 15:56:43
Статья в формате PDF
119 KB...
17 03 2024 0:47:26
Статья в формате PDF
95 KB...
16 03 2024 9:33:18
Статья в формате PDF
128 KB...
15 03 2024 4:41:32
Включение имунофана и полиоксидония в комплексное лечение детей с язвенной болезнью двенадцатипёрстной кишки обеспечивало более быструю положительную динамику клинико-лабораторных показателей и более быстрое наступление клинической ремиссии, нормализацию большинства параметров иммунологической реактивности.
...
14 03 2024 14:12:38
Предложен новый подход к изучению земного магнетизма. В центре Земли монополь µ, шаровая молния возникает в пучностях стоячих волн монополя. Гравитация – квадрупольное излучение µ.
...
13 03 2024 8:19:44
Статья в формате PDF
267 KB...
12 03 2024 17:40:45
Статья в формате PDF
351 KB...
11 03 2024 13:52:22
Статья в формате PDF
134 KB...
10 03 2024 16:10:18
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
