БИОЛОГИЧЕСКАЯ РОЛЬ СОЕДИНЕНИЙ МАРГАНЦА

Марганец - один из десяти металлов жизни и является важным биогенным элементом, который необходим для нормального протекания процессов в живых организмах. В организме взрослого человека содержится 12 мг марганца, причем 43 % этого количества находится в костях, остальное - в мягких тканях. Его недостаток приводит к заболеваниям: развивается дегенерация яичников и семенников, происходит искривление конечностей, в хрящах понижается содержание галактозамина. В биологических системах марганец присутствует в виде ионов Mn2+ или его комплексных соединений с белками, нуклеиновыми кислотами и аминокислотами. Эти комплексы входят в состав металлоферментов - аргиназы, холинэстеразы, пируваткарбоксилазы и др. Марганец участвует в таком жизненно важном процессе, как аккумуляция и перенос энергии. В организме человека биохимическим аккумулятором и переносчиком энергии являются системы АТФ и АДФ, которые в клетках находятся в виде комплексных ионов [MnАТФ]2- . Марганец усиливает действие гормонов, в том числе инсулина, а также действие ферментов, участвующих в процессах кроветворения.Марганец в виде марганца сульфата моногидрата входит в состав витаминно-минерального комплекса «Компливит» в количестве 2,5 мг на 1 таблетку. Препараты, содержащие сульфат марганца (II) и хлорид марганца (II), используют для лечения малокровия.
Соединения Мn(II) проявляют восстановительные свойства. В сильнощелочной среде окисление идет до манганатов, окрашенных в зеленый цвет, а в кислой среде - до перманганатов, имеющих малиново-фиолетовую окраску. Обнаружение марганца (II) в препаратах проводили, используя следующие реакции:
MnSO4 + 2Br2 + 8NaOH → Na2MnO4 + 4NaBr + Na2SO4 + 4H2O
3MnSO4 + 2KClO3 + 12KOH → 3K2MnO4 + 2KCl + 3К2SO4 + 6H2O
2MnSO4 + 5NaBiO3 + 16HNO3 → 2HMnO4 + 5Bi(NO3)3 + 2Na2SO4 + NaNO3 + 7H2O
2MnSO4 + 5PbO2 + 6HNO3 → 2HMnO4 + 3Pb(NO3)2 + 2PbSO4 + 2H2O.
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
19 04 2024 16:52:15
 Статья в формате PDF
228 KB...
Статья в формате PDF
228 KB...
18 04 2024 8:55:17
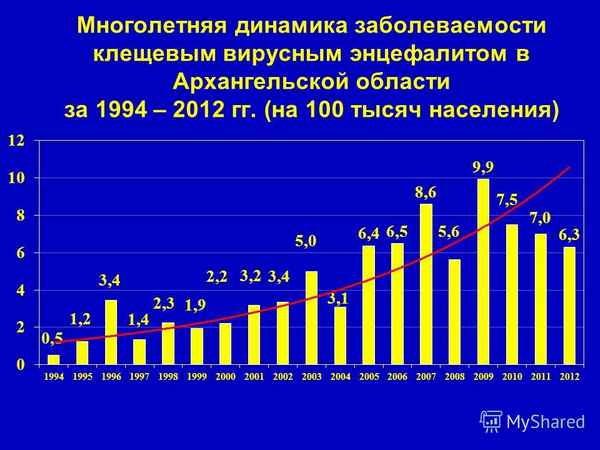 Разработана математическая модель прогнозирования инфекционной заболеваемости на модели природно-очаговой инфекции, возбудителем которой является вирус клещевого энцефалита. Математическая модель представлена в виде аддитивного временного ряда, включающая тренд, случайные компоненты и сезонные составляющие, имеющие разную периодичность: менее года, 3 года и многолетнюю.
...
Разработана математическая модель прогнозирования инфекционной заболеваемости на модели природно-очаговой инфекции, возбудителем которой является вирус клещевого энцефалита. Математическая модель представлена в виде аддитивного временного ряда, включающая тренд, случайные компоненты и сезонные составляющие, имеющие разную периодичность: менее года, 3 года и многолетнюю.
...
17 04 2024 11:12:54
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
16 04 2024 7:49:26
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
15 04 2024 23:13:21
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
13 04 2024 15:58:13
 Статья в формате PDF
516 KB...
Статья в формате PDF
516 KB...
11 04 2024 11:25:17
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
10 04 2024 23:34:42
 Статья в формате PDF
309 KB...
Статья в формате PDF
309 KB...
09 04 2024 13:12:41
 Статья в формате PDF
312 KB...
Статья в формате PDF
312 KB...
08 04 2024 23:59:33
Статья в формате PDF 138 KB...
07 04 2024 12:52:25
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
06 04 2024 20:28:16
 Статья в формате PDF
286 KB...
Статья в формате PDF
286 KB...
05 04 2024 4:15:16
Статья в формате PDF 110 KB...
04 04 2024 2:56:33
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
03 04 2024 19:52:49
 Статья в формате PDF
163 KB...
Статья в формате PDF
163 KB...
02 04 2024 11:21:16
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
01 04 2024 19:17:42
 Статья в формате PDF
163 KB...
Статья в формате PDF
163 KB...
30 03 2024 22:32:14
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
29 03 2024 18:52:57
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
28 03 2024 1:31:51
Статья в формате PDF 301 KB...
27 03 2024 4:12:18
Статья в формате PDF 250 KB...
26 03 2024 15:29:38
 Статья в формате PDF
277 KB...
Статья в формате PDF
277 KB...
25 03 2024 4:55:26
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
24 03 2024 21:57:47
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
23 03 2024 23:57:37
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
21 03 2024 8:48:38
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
20 03 2024 18:45:13
 Статья в формате PDF
161 KB...
Статья в формате PDF
161 KB...
18 03 2024 4:39:57
 Статья в формате PDF
573 KB...
Статья в формате PDF
573 KB...
17 03 2024 7:11:46
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::