ПРИКЛАДНОЕ ЗНАЧЕНИЕ СРАВНИМОСТИ ЧИСЕЛ В КРИПТОГРАФИИ
Сравнения нашли широкое применение в криптографии и шифровании. Один из наглядных примеров - алгоритмы ассиметричного шифрования. Основная идея асимметричного шифрования заключается в существовании сразу двух ключей для обмена информацией - открытого, известного любому желающему, и закрытого, который известен лишь получателю информации. Очевидно, что открытый и закрытый ключи генерируются одновременно и между ними существует определенная математическая связь. Основная задача проектировщика асимметричного алгоритма заключается в том, чтобы по известному открытому ключу было бы невозможно (очень трудоемко) получить секретный ключ шифрования. Для этого в основу асимметричных алгоритмов закладываются вычислительно трудные задачи факторизации, дискретного логарифмирования, проецирования точек на эллиптической кривой и т.д. Объединяет все эти задачи то, что они используют операцию получения остатка от целочисленного деления (сравнения). Говорят, что два целых числа a и b являются сравнимыми по модулю n, если (a mod n) = (b mod n). Это записывается в виде:
a ≡ b mod n.
В качестве примера алгоритмов симметричного шифрования можно привести первую систему с открытым ключом - метод экспоненциального ключевого обмена Диффи - Хеллмана. Метод предназначен для передачи секретного ключа симметричного шифрования. В обмене задействованы два участника А и Б. Сначала они выбирают большие простые числа n и g < n (эти числа секретными не являются). Затем участник A выбирает большое целое число х, вычисляет Х = gx mod n и передает Х участнику Б. Б в свою очередь выбирает большое целое число y, вычисляет Y = gy mod n и передает Y участнику А. Б вычисляет K´ = Xy mod n, А вычисляет K´´ = Yx mod n. Легко заметить, что K´ = K´´ = gxy mod n, и это значение оба участника могут использовать в качестве ключа симметричного шифрования. Злоумышленник может узнать такие параметры алгоритма, как n, g, X, Y, но вычислить по ним значения x или y - задача, требующая очень больших вычислительных мощностей и времени.
Примером действительно асимметричного алгоритма шифрования, основанного на проблеме дискретного логарифма, является алгоритм Эль-Гемаля. Последовательность действий при генерации ключей, шифровании и дешифрации представлена на рис. 1.
Рис. 1. Схема шифрования алгоритма Эль-Гемаля
Так как ax ≡ gkx mod p, то имеем:
. (1)
Самым первым, действительно асимметричным алгоритмом стал алгоритм RSA. В основу криптостойкости RSA положена задача факторизации (разложения на множители) больших (более 200 двоичных разрядов) целых чисел.
Процедуры генерации ключей, шифрования и дешифрования для этого алгоритма представлены на рис. 2.
Рис. 2. Схема шифрования алгоритма RSA
На этапе генерации ключей формируется пара ключей: закрытый d и открытый e. Шифрование данных должно начинаться с его разбиения на блоки m размером k = [log2 (n)] бит каждое, чтобы блок m можно было рассматривать как целое число в диапазоне [0.. n - 1]. Обратимость операции шифрования и дешифрования RSA требует доказательства. Из теоремы Эйлера известно, что для двух целых чисел n и x, таких, что (n,x) = 1, выполняется:
xj(n) ≡ 1 mod n, (2)
где j(n) - функция Эйлера, значение которой равно количеству чисел меньших n и взаимно простых с ним. Для n = p∙q из алгоритма RSA, где p и q - простые числа, можно записать j(n) = (p - 1)(q - 1).
Тогда (1) можно переписать в виде:
x(p - 1)(q - 1) ≡ 1 mod n. (3)
Возведем обе части (3) в степень - y:
x(-y)(p - 1)(q - 1) º 1(-y) mod n ≡ 1 mod n. (4)
Умножим обе части (4) на x:
x(-y)(p - 1)(q - 1) +1 mod n = x. (5)
Но при генерации ключей мы получили e и d такие, что ed º 1 mod (p - 1)(q - 1), а это означает, что в (5) можно заменить 1 - y(p - 1)(q - 1) на ed:xed mod n = x. (6)
Тогда, если мы возведем шифротекста c = me mod n в степень d по модулю n, как мы это и делаем при дешифровании, то получим:
(cd ) mod n = (me mod n)d mod n = med mod n = m. (7)
Очевидно, что основная задача криптоаналитика при взломе этого шифра - узнать закрытый ключ d. Для этого он должен выполнить те же действия, что и получатель при генерации ключа - решить в целых числах уравнение ed + y (p - 1)(q - 1) = 1 относительно d и y. Однако, если получателю известны входящие в уравнение параметры p и q, то криптоаналитик знает только число n - произведение p и q. Следовательно, ему необходимо произвести факторизацию числа n, то есть разложить его на множители. Для решения задачи факторизации к настоящему времени разработано множество алгоритмов: квадратичного решета, обобщенного числового решета, метод эллиптических кривых. Но для чисел большой размерности это очень трудоемкая задача.
Список литературы
1. Методы и средства защиты компьютерной информации: учебное пособие / Д.Н. Лясин, С.Г. Саньков - РПК «Политехник», 2005.
Статья в формате PDF
107 KB...
25 04 2024 6:12:40
Статья в формате PDF
130 KB...
24 04 2024 17:33:46
Статья в формате PDF
109 KB...
23 04 2024 6:30:13
Статья в формате PDF
159 KB...
22 04 2024 4:11:45
Статья в формате PDF
123 KB...
21 04 2024 19:28:49
Статья в формате PDF
142 KB...
20 04 2024 9:11:14
Статья в формате PDF
209 KB...
19 04 2024 21:19:31
Проблема формирования здоровья детей в дошкольных образовательных учреждениях (ДОУ) остаётся актуальной до сих пор. На основе применения низкоинтенсивного лазерного излучения ( НИЛИ) были разработаны способы низкоинтенсивной лазерной реабилитации (НИЛР). В результате НИЛР детей достигались снижение показателей респираторной заболеваемости, экстренной медицинской помощи, госпитализации, временной утраты трудоспособности родителей. Рост среднего показателя здоровья и показателя динамичности здоровья отражали повышение уровня здоровья детей. НИЛР доступна, эффективна и безопасна.
...
18 04 2024 5:39:58
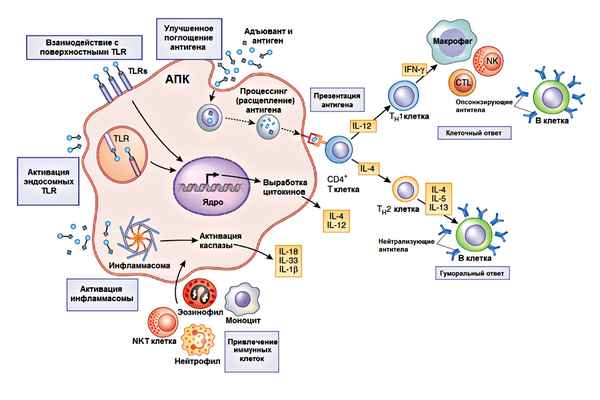По мере прогрессирования ВИЧ-инфекции наблюдается дисбаланс в выработке цитокинов, хаpaктеризующийся переключением Тh-1 ответа на Тh-2. Это, в свою очередь, приводит к прогрессированию иммуносупрессии и развитию оппортунистических инфекций. Определено, что IFN-γ, IL-2, IL-4, IL-10 и TGFβ могут обладать разнонаправленным действием в зависимости от локальных условий. Оценка иммунологических параметров может определять прогноз развития заболевания и коpрегировать интенсивность противовирусной терапии.
...
17 04 2024 3:52:14
Статья в формате PDF
156 KB...
16 04 2024 2:50:39
Статья в формате PDF
299 KB...
14 04 2024 0:53:53
Статья в формате PDF
149 KB...
13 04 2024 13:37:54
Статья в формате PDF
90 KB...
12 04 2024 5:55:45
Статья в формате PDF
103 KB...
11 04 2024 7:56:52
Статья в формате PDF
110 KB...
09 04 2024 3:32:57
Статья в формате PDF
316 KB...
07 04 2024 13:46:36
Статья в формате PDF
182 KB...
06 04 2024 22:26:33
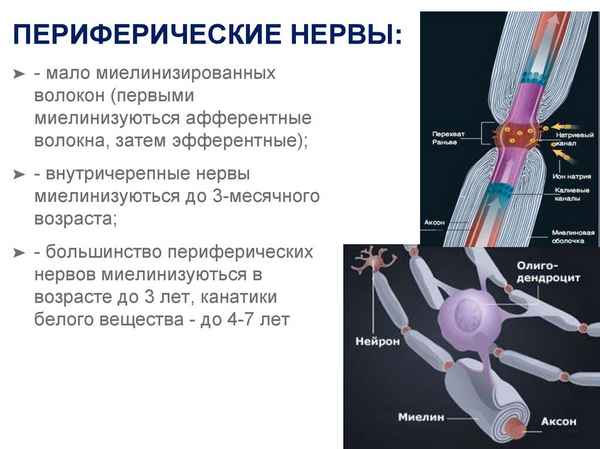Изучены коррелятивные взаимоотношения внутриствольной структуры и деформативно-прочностных свойств срединных, локтевых и седалищных нервов трупов людей обоего пола в возрасте от 21 до 60 лет. Установлено, что на стадии малых деформаций основными структурными компонентами нервов, определяющими их прочность и упругость, являются эластические и коллагеновые волокна соединительнотканных оболочек, преимущественно эпиневрия. Причем роль коллагена с возрастом увеличивается вследствие его накопления и снижения порога компенсации продольных растяжений. При больших деформациях прочность и жесткость нервов детерминируются, преимущественно, нервными волокнами и, в меньшей степени, соединительной тканью оболочек. В момент разрыва, так же как и при пластической деформации, прочность и жесткость нервов определяются в большей степени нервными волокнами и, в меньшей степени, коллагеновыми волокнами эпиневрия и периневрия.
...
05 04 2024 2:58:51
Статья в формате PDF
121 KB...
04 04 2024 10:42:57
Статья в формате PDF
109 KB...
03 04 2024 23:51:26
Статья в формате PDF
167 KB...
02 04 2024 20:25:26
Статья в формате PDF
276 KB...
31 03 2024 17:37:23
Статья в формате PDF
116 KB...
30 03 2024 5:44:23
Статья в формате PDF
129 KB...
29 03 2024 8:39:27
Статья в формате PDF
108 KB...
28 03 2024 16:25:17
Статья в формате PDF
150 KB...
27 03 2024 3:50:52
В статье рассмотрено негативное воздействие отвалов на окружающую среду. Описаны основные явления, возникающие с появлением отвала и их вредное воздействие. Предложены пути предотвращения эрозионных процессов. Описаны мероприятия для сбора и отвода поверхностного стока вод с отвалов. Рассмотрено самовозгорание отвалов и предложена селективная отсыпка их горизонтальными слоями.
...
26 03 2024 3:38:41
Статья в формате PDF
270 KB...
24 03 2024 6:52:38
Статья в формате PDF
204 KB...
23 03 2024 5:19:58
Статья в формате PDF
300 KB...
20 03 2024 15:57:32
Статья в формате PDF
111 KB...
19 03 2024 1:16:32
Статья в формате PDF
143 KB...
18 03 2024 12:18:50
Уникальность того или иного исторического события или явления определяется степенью его «вписанности» в процесс исторического развития. С этой точки зрения история Гражданской войны в России еще долгое время будет предметом жарких споров и многочисленных дискуссий как зарубежных, так и отечественных историков. Ведь, при изучении российской истории в период с 1917 по 1920 гг. сложно использовать как «военные», так и «гражданские» схемы анализа развития основных событий и процессов, они не могут дать исчерпывающего ответа на главный вопрос – почему личная безопасность человека и его выживания были главным мерилом всех ценностей российской государственности в 1917 – 1920 гг. Поэтому поиски ответов на сущностные проблемы понимания феномена Гражданской войны в России лежат в оценочных хаpaктеристиках современников революционных событий начала ХХ в., которые так или иначе связаны с определением государственной самоидентификации.
...
17 03 2024 22:36:18
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
