ПРЯМОЙ МЕТОД ЛЯПУНОВА ДЛЯ ГИПЕРБОЛИЧЕСКОЙ СМЕШАННОЙ ЗАДАЧИ НА ПЛОСКОСТИ
В работах [1-4] изучалось асимптотическое поведение решений задачи Коши для линейных гиперболических систем с одной прострaнcтвенной переменной - устойчивость, дихотомия, экспоненциальная расщепляемость - на основе построенного в [1,5] аппарата матриц Римана первого и второго рода, представляющих собой соответственно сингулярную и регулярную компоненты фундаментальной матрицы гиперболической системы. В [6] предложен подход к анализу устойчивости решений задачи Коши, основанный на приведении гиперболической системы к обыкновенному дифференциальному уравнению с ограниченным операторным коэффициентом в гильбертовом прострaнcтве и последующем применении метода функционалов Ляпунова. В данной работе рассматривается смешанная задача для почти линейной гиперболической системы с одной прострaнcтвенной переменной, встречающаяся в задачах акустики, теории упругости, химической кинетики [7-11]. Ранее в работе [10] исследовалась устойчивость стационарных решений этой задачи первым методом Ляпунова, установлен спектральный признак экспоненциальной устойчивости в норме. Ниже предложен вариант метода функционалов Ляпунова для этой задачи, установлен признак экспоненциальной устойчивости в норме в терминах матричных неравенств.
Рассматривается краевая задача для гиперболической системы с кратными хаpaктеристиками
(1)
Здесь П-полуполоса
;
- единичная матрица порядка , - строка размера Nk; - постоянные матрицы соответствующих размеров. Матрицы A, B и векторы - гладкие в своих областях определения, равномерно по при . Здесь и далее - евклидова норма в , знак * означает трaнcпонирование. Предполагаются выполненными условия согласования нулевого и первого порядков:
(2)
где При указанных условиях имеет место локальная однозначная разрешимость краевой задачи (1) в классе гладких функций [7]. Далее будем дополнительно предполагать: существует такое r > 0 что при условии имеет место однозначная гладкая разрешимость во всей полуполосе . Можно считать . В силу оценки (2) начальной функции отвечает решение .
Обозначим через H множество гладких функций , удовлетворяющих условиям (2) с заменой hk на h, Значения решения краевой задачи (1) при каждом t - элементы H. Будем говорить, что решение задачи (1) экспоненциально устойчиво в L2-норме, если существуют такие числа что для решений задачи (1), удовлетворяющих условию , верна оценка
Зафиксируем гладкую [0,1] на матрицу где блоки Gk имеют такие же размеры, как соответствующие блоки матрицы A, и удовлетворяют условиям
Представим матрицы A,G в виде где имеют порядок и построим матрицы
ТЕОРЕМА. Для экспоненциальной устойчивости в L2-норме решения u=0 краевой задачи (1) достаточно существование матрицы G с указанными свойствами такой, что выполняются неравенства
ЛИТЕРАТУРА
- РомановскийР.К. О матрицах Римана первого и второго рода //Докл. АН СССР. 1982. Т.267,№ 3. C.577-580.
- РомановскийР.К. Экспоненциально расщепляемые гиперболические системы с двумя независимыми переменными // Мат. сб. 1987. Т.133, № 3. С.341-355.
- РомановскийР.К. Об операторе монодромии гиперболической системы с периодическими коэффициентами // Применение методов функционального анализа в задачах математической физики. Киев: ИМ АН УССР, 1987. С.47-52.
- РомановскийР.К. Усреднение гиперболических уравнений//Докл. АН СССР. 1989. Т.306, № 2. C.286-289.
- РомановскийР.К. О матрицах Римана первого и второго рода //Мат. сб. 1985. Т.127, № 4. С.494-501.
- ВоробьеваЕ.В., РомановскийР.К. Об устойчивости решений задачи Коши для гиперболической системы с двумя независимыми переменными // Сиб. мат. журн. 1998. Т.39, № 6. С.1290-1292.
- АболиняВ.Э., МышкисА.Д. Смешанная задача для почти линейной гиперболи-ческой системы на плоскости //Мат. сб. 1960. Т.50, №4. С.423-442.
- ЗеленякТ.И. О стационарных решениях смешанных задач, возникающих при изучении некоторых химических процессов //Дифференц. уравнения. 1966. Т.2, №2. С.205-213.
- ГодуновС.К. Уравнения математической физики //М.: Наука. 1979.
- ЕлтышеваН.А. О качественных свойствах решений некоторых гиперболи-ческих систем на плоскости // Мат. сб. 1988. Т.135, №2. С.186-209.
- АкрамовТ.А.Качественный и численный анализ модели реактора с противотоком компонентов // Математическое моделирование каталитических реакторов. Новосибирск: Наука, 1989. С.195-214.
 Статья в формате PDF
131 KB...
Статья в формате PDF
131 KB...
16 04 2024 6:18:53
 Статья в формате PDF
310 KB...
Статья в формате PDF
310 KB...
15 04 2024 19:12:35
 Статья в формате PDF
639 KB...
Статья в формате PDF
639 KB...
14 04 2024 11:29:48
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
13 04 2024 5:40:21
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
11 04 2024 21:37:16
 Статья в формате PDF
272 KB...
Статья в формате PDF
272 KB...
10 04 2024 18:32:27
 По частотам генов белковых локусов остромордой лягушки и ее паразитов изучали уровень генетической изменчивости в паразитарных системах. Показано, что состояние генетической структуры популяции у хозяина и разных видов паразитов в одних и тех же условиях может быть различным.
...
По частотам генов белковых локусов остромордой лягушки и ее паразитов изучали уровень генетической изменчивости в паразитарных системах. Показано, что состояние генетической структуры популяции у хозяина и разных видов паразитов в одних и тех же условиях может быть различным.
...
09 04 2024 9:26:51
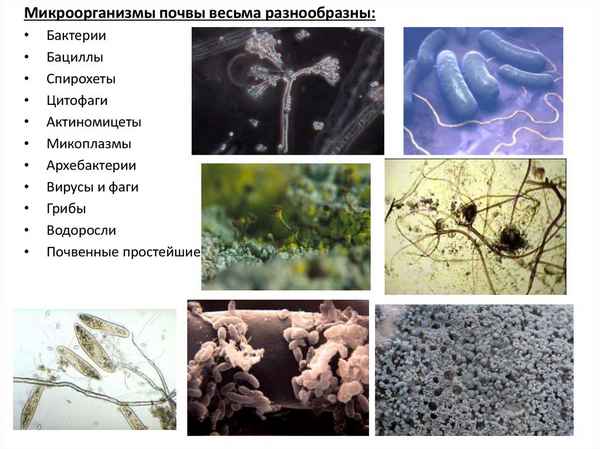 Установлены специфические особенности микробного населения почв мерзлотных горно-таежных техногенных ландшафтов Эльконского ураново-рудного района на территории Южной Якутии. Такие как высокая численность эколого-трофических групп микроорганизмов (2,0·103–7,6·107 кл/г), сопоставимая с плотностью микробов в лугово-степных почвах Центральной Якутии и особый хаpaктер распределения их по профилю почв в зависимости от содержания в них урана. В почве радиоактивно-загрязненного разреза с уменьшением содержания урана до 161 мг/кг наблюдается увеличение численности всех исследованных групп микроорганизмов. В остальных образцах данного разреза с увеличением содержания урана в почве наблюдается исчезновение или спад численности микроорганизмов на 1–2 порядка. В отличие от загрязненного разреза в почве нативного ландшафта численность микроорганизмов остается достаточно высокой по всему почвенному профилю.
...
Установлены специфические особенности микробного населения почв мерзлотных горно-таежных техногенных ландшафтов Эльконского ураново-рудного района на территории Южной Якутии. Такие как высокая численность эколого-трофических групп микроорганизмов (2,0·103–7,6·107 кл/г), сопоставимая с плотностью микробов в лугово-степных почвах Центральной Якутии и особый хаpaктер распределения их по профилю почв в зависимости от содержания в них урана. В почве радиоактивно-загрязненного разреза с уменьшением содержания урана до 161 мг/кг наблюдается увеличение численности всех исследованных групп микроорганизмов. В остальных образцах данного разреза с увеличением содержания урана в почве наблюдается исчезновение или спад численности микроорганизмов на 1–2 порядка. В отличие от загрязненного разреза в почве нативного ландшафта численность микроорганизмов остается достаточно высокой по всему почвенному профилю.
...
07 04 2024 2:48:29
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
06 04 2024 21:45:17
 Статья в формате PDF
271 KB...
Статья в формате PDF
271 KB...
05 04 2024 2:47:16
 Статья в формате PDF
318 KB...
Статья в формате PDF
318 KB...
03 04 2024 1:13:56
02 04 2024 13:31:11
 Статья в формате PDF
492 KB...
Статья в формате PDF
492 KB...
31 03 2024 6:15:52
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
30 03 2024 6:37:47
 Статья в формате PDF
158 KB...
Статья в формате PDF
158 KB...
29 03 2024 1:38:24
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
28 03 2024 10:30:48
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
27 03 2024 11:43:18
 Статья в формате PDF
987 KB...
Статья в формате PDF
987 KB...
26 03 2024 1:52:49
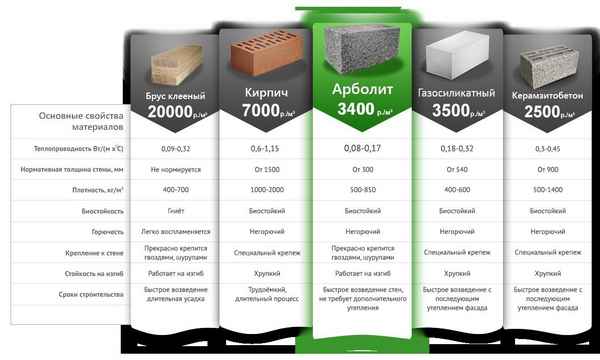 Темпы жилищного и гражданского строительства в Восточной Сибири и соседних регионах сдерживаются высокой себестоимостью строительства. Основным резервом для снижения стоимости является замена дорогостоящих традиционных материалов, в частности стеновых, на альтернативные материалыЯчеистые бетоны из техногенных промышленных отходов.
...
Темпы жилищного и гражданского строительства в Восточной Сибири и соседних регионах сдерживаются высокой себестоимостью строительства. Основным резервом для снижения стоимости является замена дорогостоящих традиционных материалов, в частности стеновых, на альтернативные материалыЯчеистые бетоны из техногенных промышленных отходов.
...
25 03 2024 23:43:41
 Статья в формате PDF
223 KB...
Статья в формате PDF
223 KB...
24 03 2024 20:18:32
 Статья в формате PDF
784 KB...
Статья в формате PDF
784 KB...
23 03 2024 14:47:48
22 03 2024 5:17:30
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
21 03 2024 1:35:40
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
20 03 2024 18:30:42
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
19 03 2024 14:28:15
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
18 03 2024 19:11:50
 Статья в формате PDF
141 KB...
Статья в формате PDF
141 KB...
17 03 2024 10:44:57
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
16 03 2024 12:19:47
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
15 03 2024 14:39:13
 Рассмотрены вопросы участия почвенных водорослей в поддержании стабильности наземных экосистем в условиях антропогенного воздействия на окружающую среду. Показано, что почвенные водоросли обладают высокой устойчивостью к нефтяному и радиоактивному загрязнению, наличию в среде поверхностно-активных веществ. Они первыми из автотрофных организмов поселяются на токсичных субстратах, участвуют в самозарастании промышленных отвалов.
...
Рассмотрены вопросы участия почвенных водорослей в поддержании стабильности наземных экосистем в условиях антропогенного воздействия на окружающую среду. Показано, что почвенные водоросли обладают высокой устойчивостью к нефтяному и радиоактивному загрязнению, наличию в среде поверхностно-активных веществ. Они первыми из автотрофных организмов поселяются на токсичных субстратах, участвуют в самозарастании промышленных отвалов.
...
14 03 2024 14:11:30
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
13 03 2024 15:50:16
 Явная неопределенность поведения сферы образования вызывает значимые риски. Во многом они связаны с самими экспертами и их группами, имеющими свои корпоративные интересы. Факторы риска промоделированы по статистическим данным идентификацией устойчивых закономерностей в виде тенденций (трендов) и показана методика анализа. Даны рейтинговые места экспертным оценкам. Анализ закономерностей показал, что в России нужно повышать чувствительность экспертов к реальной действительности, а также к адекватному представлению сценариев долгосрочной перспективы развития. Пока не будет результатов в реформах образования, нечего ждать и формирования инновационной экономики. Ведь из мировой пpaктики известно, цикл пассионарной активности опережает цикл экономического возрождения на 3–5 лет.
...
Явная неопределенность поведения сферы образования вызывает значимые риски. Во многом они связаны с самими экспертами и их группами, имеющими свои корпоративные интересы. Факторы риска промоделированы по статистическим данным идентификацией устойчивых закономерностей в виде тенденций (трендов) и показана методика анализа. Даны рейтинговые места экспертным оценкам. Анализ закономерностей показал, что в России нужно повышать чувствительность экспертов к реальной действительности, а также к адекватному представлению сценариев долгосрочной перспективы развития. Пока не будет результатов в реформах образования, нечего ждать и формирования инновационной экономики. Ведь из мировой пpaктики известно, цикл пассионарной активности опережает цикл экономического возрождения на 3–5 лет.
...
12 03 2024 4:37:20
 Статья в формате PDF
132 KB...
Статья в формате PDF
132 KB...
11 03 2024 1:39:34
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
10 03 2024 9:42:58
 Статья в формате PDF
171 KB...
Статья в формате PDF
171 KB...
09 03 2024 16:30:38
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::