ОПРЕДЕЛЕНИЕ НАГРУЗКИ И ФОРМЫ ПОВЕРХНОСТИ ОСНАСТКИ ПРИ ФОРМООБРАЗОВАНИИ ДЕТАЛЕЙ

Математическая модель, описывающая процесс формообразования неупругих тел строится на базе двух следующих интегральных уравнений.
1. Вариационное уравнение для работы деформаций, в которое входят:
тензор напряжения Коши; текущие изменяемые в процессе деформирования объем тела и его поверхность; тензор четвертого ранга, ответственный за упругопластические свойства материала.
2. Вариационное неравенство для формулировки условий на границах контакта детали и рабочей поверхности матрицы (пуансона).
При формировании тензора свойств материалов в качестве физических соотношений принимались соотношения ассоциированного закона пластического течения между тензором напряжения Коши и приращением тензора деформации Альманси. Поверхность текучести описывалась условием Мизеса с изотропным и трaнcляционным упрочнением материала.
Геометрическая нелинейность учитывалась, во-первых, в соотношениях между логарифмическим тензором деформации Генки и вектором перемещений; во-вторых, при формулировке принципа материальной объективности в физических соотношениях; в третьих, в перестройке конфигурации тела в процессе его деформирования.
Тензор Генки представлялся разложением в степенной ряд тензора деформации Альманси.
Для реализации решения задачи использовался метод конечных элементов, благодаря которому приведенные выше интегральные уравнения сведены к нелинейным матричным. При реализации решения задач на ЭВМ использован метод последовательных нагружений с внутренним итерационным циклом и использованием модифицированного метода Ньютона-Рафсона.
Алгоритмы управления распределением поверхностной нагрузки, требуемой для получения, например, равнотолщинных тонкостенных деталей или для определения формы рабочих поверхностей матриц (пуансонов) с целью получения детали заданной конфигурации (с учетом пружинения), строились на базе решения обратных задач механики деформирования.
Упомянутые обратные задачи решались методом последовательных приближений с корректировкой решения на каждой итерации для получения необходимых функций.
Литература
- Горлач Б.А. Математическое моделирование процессов формообразования неупругих тел. -- М., Изд. МАИ, 1999, -- 216 с.
 Статья в формате PDF
308 KB...
Статья в формате PDF
308 KB...
27 04 2024 5:39:52
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
26 04 2024 17:17:39
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
25 04 2024 18:12:30
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
24 04 2024 2:29:46
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
23 04 2024 10:15:19
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
22 04 2024 22:24:15
 Статья в формате PDF
287 KB...
Статья в формате PDF
287 KB...
20 04 2024 19:26:16
 Статья в формате PDF
276 KB...
Статья в формате PDF
276 KB...
19 04 2024 23:36:46
 Статья в формате PDF
128 KB...
Статья в формате PDF
128 KB...
18 04 2024 20:29:58
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
17 04 2024 2:29:58
 Статья в формате PDF
293 KB...
Статья в формате PDF
293 KB...
16 04 2024 17:13:20
 Статья в формате PDF
263 KB...
Статья в формате PDF
263 KB...
15 04 2024 1:27:10
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
14 04 2024 9:19:17
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
13 04 2024 11:26:36
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
12 04 2024 0:33:31
Статья в формате PDF 327 KB...
11 04 2024 9:44:11
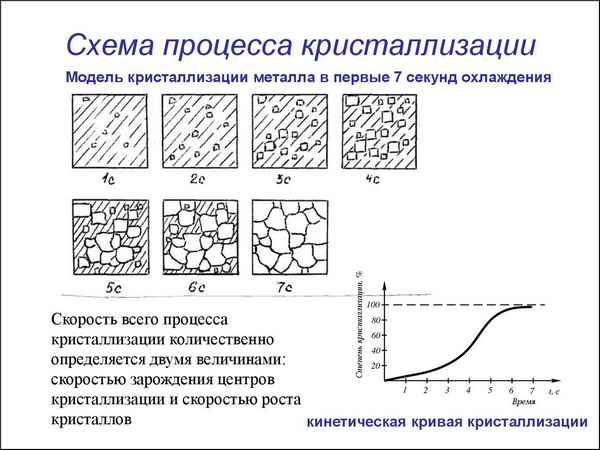 Надежность кристаллизационных установок можно обеспечивать, учитывая, что при ведении основного процесса протекают побочные процессы (агломерация кристаллов, их дробление, инкрустация, вторичное образование зародышей и др.).
...
Надежность кристаллизационных установок можно обеспечивать, учитывая, что при ведении основного процесса протекают побочные процессы (агломерация кристаллов, их дробление, инкрустация, вторичное образование зародышей и др.).
...
10 04 2024 14:10:35
 Статья в формате PDF
204 KB...
Статья в формате PDF
204 KB...
09 04 2024 20:55:27
 Статья в формате PDF
217 KB...
Статья в формате PDF
217 KB...
08 04 2024 2:25:55
07 04 2024 6:36:21
 Статья в формате PDF
384 KB...
Статья в формате PDF
384 KB...
05 04 2024 7:32:39
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
04 04 2024 16:33:44
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
03 04 2024 16:37:28
 Статья в формате PDF
128 KB...
Статья в формате PDF
128 KB...
02 04 2024 0:58:52
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
01 04 2024 20:34:25
 Статья в формате PDF
219 KB...
Статья в формате PDF
219 KB...
31 03 2024 21:31:26
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
30 03 2024 22:13:45
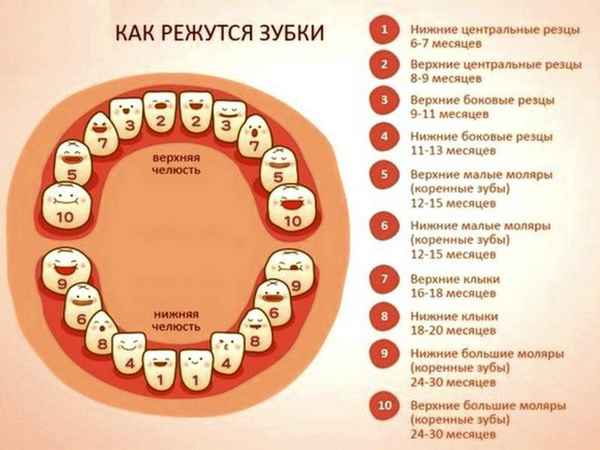 В настоящее время основной задачей стоматологии является профилактика кариеса, особенно для возрастной группы 11-16 лет. Ранее была установлена связь между кариесом и аномалиями зубочелюстной деформацией системы.
В 2001-2002 г нами было обследовано 2504 ребенка в возрасте от 11 до 16 лет.
Из них 1016 (40,6%) мальчиков и 1488 (59,4%) девочек.
Из числа выявленных аномалий прикуса чаще наблюдался глубокий прикус, затем дистальный, осложненный открытым прикусом, мезиальный и открытый, остальные виды прикусов встречались крайне редко.
На основе компьютерной обработке полученных данных очевидно, что деформация зубочелюстной системы встречается в возрастных группах со сменным и постоянным прикусом;
- аномалии прикуса составляют 53% от общего количества обследованных детей;
- аномалии положения отдельных зубов составляют 39% от общего количества обследованных детей.
...
В настоящее время основной задачей стоматологии является профилактика кариеса, особенно для возрастной группы 11-16 лет. Ранее была установлена связь между кариесом и аномалиями зубочелюстной деформацией системы.
В 2001-2002 г нами было обследовано 2504 ребенка в возрасте от 11 до 16 лет.
Из них 1016 (40,6%) мальчиков и 1488 (59,4%) девочек.
Из числа выявленных аномалий прикуса чаще наблюдался глубокий прикус, затем дистальный, осложненный открытым прикусом, мезиальный и открытый, остальные виды прикусов встречались крайне редко.
На основе компьютерной обработке полученных данных очевидно, что деформация зубочелюстной системы встречается в возрастных группах со сменным и постоянным прикусом;
- аномалии прикуса составляют 53% от общего количества обследованных детей;
- аномалии положения отдельных зубов составляют 39% от общего количества обследованных детей.
...
29 03 2024 23:41:13
 Статья в формате PDF
207 KB...
Статья в формате PDF
207 KB...
28 03 2024 12:38:51
 Статья в формате PDF
255 KB...
Статья в формате PDF
255 KB...
27 03 2024 21:43:15
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
26 03 2024 21:24:18
 В работе показано, что фундаментальные принципы классической механики и теории поля - принцип наименьшего действия и калибровочная инвариантность полей и электромагнитного поля - есть прямое следствие существования уже в рамках классической физики функции состояния.
...
В работе показано, что фундаментальные принципы классической механики и теории поля - принцип наименьшего действия и калибровочная инвариантность полей и электромагнитного поля - есть прямое следствие существования уже в рамках классической физики функции состояния.
...
25 03 2024 19:58:43
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
22 03 2024 1:25:45
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
21 03 2024 7:29:27
20 03 2024 9:15:41
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
19 03 2024 19:42:55
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::