МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ КРУГОВОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ С ИДЕАЛЬНОЙ СЖИМАЕМОЙ ЖИДКОСТЬЮ

В работе рассматриваются вынужденные колебания круговой цилиндрической оболочки конечных размеров в идеальной сжимаемой жидкости. Для решения полученной системы интегрального и дифференциального уравнений применен метод разложения решения в ряд по собственным формам колебаний оболочки в вакууме и метод ортогональных многочлeнов. Проведено численное исследование полученных результатов.
Задачи гидроупругости представляют большой теоретический и пpaктический интерес. При исследовании этих задач появляется возможность выявить взаимное влияние жидкости и контактирующей с ней упругой конструкции. В [1] даны постановки и методы решения широкого круга задач гидроупругости, приведен список литературы, отражающий положение дел в рассматриваемой области.
Пусть упругая круговая цилиндрическая оболочка длины 2a, радиуса R помещена в идеальную сжимаемую жидкость, занимающую безграничный объем. Ось Oz цилиндрической системы координат r, θ, z направим вдоль оси оболочки. При исследовании взаимодействия оболочки с жидкостью будем исходить из уравнения технической теории оболочек [2]:
(1)
Здесь E - модуль Юнга, ν - коэффициент Пуассона, h - толщина оболочки, w = w(z,t) - радиальное перемещение точек срединной поверхности оболочки,
ρ0 - плотность оболочки, p = p(r, z, t) - гидродинамическое давление.
Жесткость оболочки при изгибе D связана с параметрами E, ν, и h формулой:
(2)
Перемещения, направленные к оси оболочки, считаются положительными. На торцах оболочки считаем заданными радиальные перемещения и углы поворота. Граничные условия имеют вид:
(3)
где С1, С2 = const
Движение жидкости предполагается потенциальным. Потенциал скоростей точек жидкости φ = φ(r,z,t) удовлетворяет волновому уравнению
(4)
Здесь с - скорость звука в жидкости.
Гидродинамическое давление p в предположении малости вносимых оболочкой возмущений связано с функцией φ интегралом Коши, который в линеаризованной форме имеет вид
(5)
где ρ - плотность жидкости, p∞ - давление на бесконечности.
(6)
Условие безотрывного обтекания оболочки имеет вид:
Будем предполагать справедливым следующее представление функций
(7)
Получили систему двух уравнений в безразмерном виде:
(8)
Где
а S - число Струхала
В уравнении (8) и далее знаки «штрих», «волна» и «звездочка» опущены.
В соответствии с условием излучения Зоммерфельда необходимо, чтобы решение содержало волны, уходящие на бесконечность и не содержало волны, приходящие из бесконечности. Для отбора такого решения контур Г был выбран следующим образом:
Выбор контура Г
Отсюда, однозначные ветви, соответствующие обходу точек ветвления, взяты в виде:
. (9)
Учитывая, линейность полученных уравнений, функцию w будем искать в виде функционального ряда:
(10)
где ψn(z) выражаются формулой
(11)
а ξn определяется из уравнения
(12)
Отметим, что
(13)
В силу линейности задачи γ тоже представим в функционального ряда:
(14)
Представления (10) и (14) позволяют разделить систему уравнений (8) и рассматривать каждое из них отдельно. Преобразуем интегральное уравнение и рассмотрим его относительно γn при известных правых частях.
(15)
Приравняем слагаемые при Xn
(16)
Главную часть ядра интегрального уравнения (16) можно получить, учитывая обобщенное значение интеграла
(17)
Тогда решение интегрального уравнения (16) целесообразно строить в виде:
(18)
Применение процедуры метода ортогональных многочлeнов к уравнению (16), сводит это уравнение к СЛАУ относительно Хn
(19)
Подставим найденные Хn в
Непосредственные вычисления были проведены с использованием метода редукции.
При этом для получения решения с достаточной для пpaктического использования точностью при 2 ≤ λ < ∞ можно ограничится решением урезанных систем состоящих из шести уравнений. В табл. 1 приведены значения функции |w* (z)| на частоте ω = 10 для случая несжимаемой жидкости (S = 0), соответствующие М = 3, 4, 5, 6, где М - порядок урезанной системы (19).
1. Значения функции |w* (z)| при α = 1000, β = 30, λ = 2, ω = 10, S = 0
|
z M |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
3 |
1,97357 |
1,26168 |
0,34574 |
1,61614 |
1,62038 |
0,99999 |
|
4 |
2,15145 |
1,34339 |
0,42596 |
1,73302 |
1,66494 |
0,99999 |
|
5 |
2,15479 |
1,34371 |
0,42815 |
1,73327 |
1,66484 |
0,99999 |
|
6 |
2,15485 |
1,34369 |
0,42817 |
1,73325 |
1,66484 |
0,99999 |
В табл. 2 приведены значения функции |w*(z)| на частоте ω = 10 при для случая сжимаемой жидкости (S = 1), соответствующие М = 3, 4, 5, 6, где М - порядок урезанной системы (19).
2. Значения функции |w*(z)| при α = 1000, β = 30, λ = 2, ω = 10, S = 1
|
Z M |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
3 |
3,80923 |
2,38121 |
0,77378 |
3,03780 |
2,52649 |
0,99999 |
|
4 |
4,23417 |
2,58308 |
0,95095 |
3,30801 |
2,63233 |
0,99999 |
|
5 |
4,24139 |
2,58387 |
0,95555 |
3,30859 |
2,63214 |
0,99999 |
|
6 |
4,24152 |
2,58382 |
0,95561 |
3,30854 |
2,63216 |
0,99999 |
На основании проведенных вычислений для различных значений приведенной частоты ω можно сделать выводы, что в рассмотренном диапазоне изменения параметров метод редукции сходится достаточно хорошо, с увеличением частоты увеличивается количество максимумов функции W по длине оболочки.
Список литературы
- Горшков А.Г., Морозов В.И., Пономарев А.Т., Шклярчук Ф.Н. Аэрогидроупругость конструкций. - М.: Физматлит, 2000. - 592 с.
- Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. - М.: Физматгиз, 1963. - 636 с.
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
09 03 2026 14:21:39
 Статья в формате PDF
272 KB...
Статья в формате PDF
272 KB...
07 03 2026 10:11:21
 Статья в формате PDF
249 KB...
Статья в формате PDF
249 KB...
06 03 2026 20:18:48
 Статья в формате PDF
250 KB...
Статья в формате PDF
250 KB...
05 03 2026 14:56:41
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
04 03 2026 12:10:34
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
02 03 2026 16:16:40
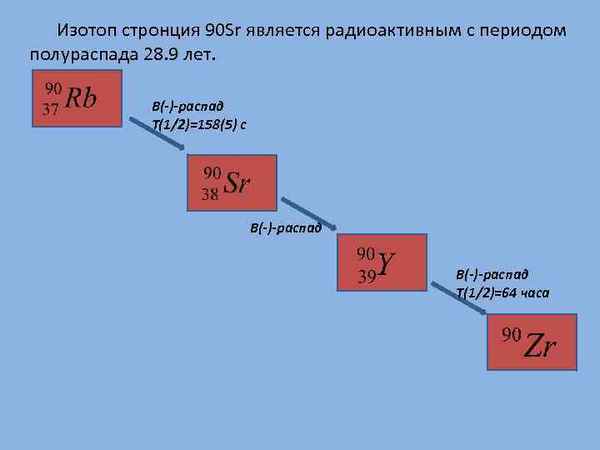 Приведены данные по концентрациям и соотношениям изтопов стронция и неодима в шошонитовых гранитоидах Алтае-Саянской складчатой области, Большого Кавказа, Британских каледонид, Шотландии, Западного Кунь-Луня, Бразилии. Выделены 4 подтипа гранитоидов, различающихся степенями изотопной обогощённости и деплетированности. По соотношениям 87Sr/86Sr отмечены широкие вариации значений от 0,7022 (мантийные значения) до 0,712958 (компонент обогащённой мантии c контаминацией корового материала). Все подтипы шошонитовых гранитоидов тяготеют к компонентам обогащённой мантии типов EM I и EM II. Это связывается с допущением о вовлечении в субдукционный процесс нижней части континентальной литосферы, или с субдуцированием в мантию терригенных осадков.
...
Приведены данные по концентрациям и соотношениям изтопов стронция и неодима в шошонитовых гранитоидах Алтае-Саянской складчатой области, Большого Кавказа, Британских каледонид, Шотландии, Западного Кунь-Луня, Бразилии. Выделены 4 подтипа гранитоидов, различающихся степенями изотопной обогощённости и деплетированности. По соотношениям 87Sr/86Sr отмечены широкие вариации значений от 0,7022 (мантийные значения) до 0,712958 (компонент обогащённой мантии c контаминацией корового материала). Все подтипы шошонитовых гранитоидов тяготеют к компонентам обогащённой мантии типов EM I и EM II. Это связывается с допущением о вовлечении в субдукционный процесс нижней части континентальной литосферы, или с субдуцированием в мантию терригенных осадков.
...
01 03 2026 5:34:33
 Статья в формате PDF
251 KB...
Статья в формате PDF
251 KB...
28 02 2026 18:16:31
Статья в формате PDF 279 KB...
27 02 2026 2:12:46
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
26 02 2026 2:48:59
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
24 02 2026 13:24:25
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
23 02 2026 20:26:33
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
22 02 2026 5:13:34
 Экспериментальные исследования на участке распространения пород ледового комплекса выявили увеличение глубины сезонного протаивания и повышение температуры грунтов на прилегающей к железной дороге просеке. Установлено поднятие верхней границы многолетнемерзлых пород под высокой насыпью и низкой насыпью с теплоизолирующим материалом, отсыпанных в зимний сезон. Отмечено формирование чаши протаивания при отсыпке нулевой насыпи в теплый период с удалением сезонноталого слоя в её основания. Предложены мероприятия обеспечивающие устойчивость земляного полотна.
...
Экспериментальные исследования на участке распространения пород ледового комплекса выявили увеличение глубины сезонного протаивания и повышение температуры грунтов на прилегающей к железной дороге просеке. Установлено поднятие верхней границы многолетнемерзлых пород под высокой насыпью и низкой насыпью с теплоизолирующим материалом, отсыпанных в зимний сезон. Отмечено формирование чаши протаивания при отсыпке нулевой насыпи в теплый период с удалением сезонноталого слоя в её основания. Предложены мероприятия обеспечивающие устойчивость земляного полотна.
...
21 02 2026 13:53:32
 Статья в формате PDF
144 KB...
Статья в формате PDF
144 KB...
20 02 2026 13:27:15
 Статья в формате PDF
215 KB...
Статья в формате PDF
215 KB...
19 02 2026 10:40:18
 Статья в формате PDF
367 KB...
Статья в формате PDF
367 KB...
18 02 2026 9:13:50
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
17 02 2026 9:35:30
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
16 02 2026 9:14:50
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
15 02 2026 18:46:48
13 02 2026 13:21:28
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
12 02 2026 9:23:48
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
11 02 2026 0:50:56
 Уровень жизни и социально-экономические условия жизни – важнейшие хаpaктеристики общества. Статья посвящена анализу дифференциации и динамике этих хаpaктеристик по муниципальным образованиям Саратовской области с использованием метода композиционного индекса.
...
Уровень жизни и социально-экономические условия жизни – важнейшие хаpaктеристики общества. Статья посвящена анализу дифференциации и динамике этих хаpaктеристик по муниципальным образованиям Саратовской области с использованием метода композиционного индекса.
...
10 02 2026 5:27:25
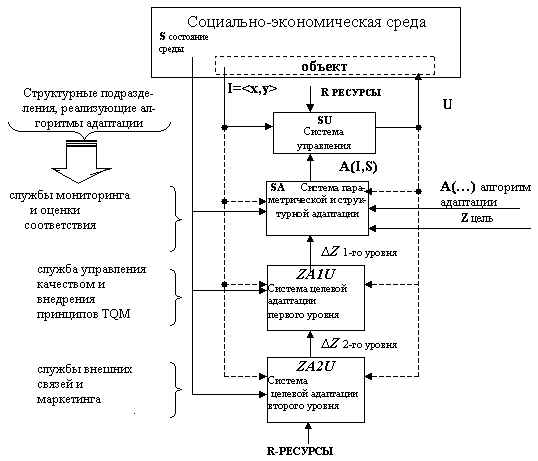 Поднятые в данной работе проблемы повышения конкурентоспособности предприятия позволяют сформулировать научные подходы к определению концепции управления хозяйствующими субъектами в широком использовании механизма адаптации промышленных предприятий в условиях изменяющейся рыночной среды. В результате анализа соотношения адаптационных процессов и организационной структуры сделан вывод о наиболее эффективной форме адаптивного управления – многомерной организационной структуре, которая позволяет повысить адаптивность организации и ее способность реагировать на изменение внутренних и внешних условий. Это достигается путем разбиения организации на подразделения, жизнеспособность которых зависит от их умения производить по конкурентоспособным ценам товары, пользующиеся спросом, и предоставлять услуги, в которых нуждаются потребителя.
...
Поднятые в данной работе проблемы повышения конкурентоспособности предприятия позволяют сформулировать научные подходы к определению концепции управления хозяйствующими субъектами в широком использовании механизма адаптации промышленных предприятий в условиях изменяющейся рыночной среды. В результате анализа соотношения адаптационных процессов и организационной структуры сделан вывод о наиболее эффективной форме адаптивного управления – многомерной организационной структуре, которая позволяет повысить адаптивность организации и ее способность реагировать на изменение внутренних и внешних условий. Это достигается путем разбиения организации на подразделения, жизнеспособность которых зависит от их умения производить по конкурентоспособным ценам товары, пользующиеся спросом, и предоставлять услуги, в которых нуждаются потребителя.
...
09 02 2026 17:53:48
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
08 02 2026 21:15:30
 Статья в формате PDF
145 KB...
Статья в формате PDF
145 KB...
07 02 2026 0:33:22
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
06 02 2026 8:20:47
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
05 02 2026 7:44:15
 Статья в формате PDF
3943 KB...
Статья в формате PDF
3943 KB...
04 02 2026 2:45:57
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
01 02 2026 21:29:33
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
31 01 2026 15:54:58
 Статья в формате PDF
182 KB...
Статья в формате PDF
182 KB...
30 01 2026 3:15:37
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
29 01 2026 11:17:18
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::