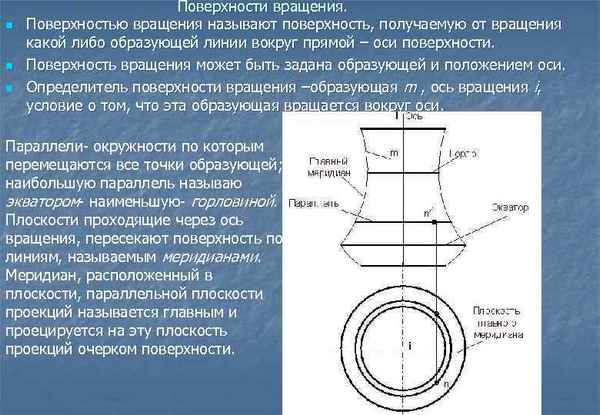
Теорема о количестве и структуре особых точек n–мерной динамической системы популяционной динамики Лотки-Вольтерра в контексте информационного анализа и моделирования
1 ФГБОУ ВО «Воронежский государственный педагогический университет» С помощью элементарных методов комбинаторной математики и единственности решений систем линейных алгебраических уравнений для невырожденных случаев доказана теорема о количестве и структуре особых точек n–мерной динамической системы популяционной динамики Лотки-Вольтерра. Показано, что количество особых точек для этой системы равняется 2n, а их структура в отношении сочетания нулевых и ненулевых координат совпадает с биноминальными коэффициентами. Сделано предположение, что с помощью этой динамической системы можно моделировать конкурентные взаимодействия среди n научных фронтов в рамках широкой области научных исследований. Статья в формате PDF 372 KB модель Лотки-Вольтеррапопуляционная динамикаколичество особых точекбиноминальные коэффициентырешения систем линейных алгебраических уравнений 1. Вольтерра В. Математическая теория борьбы за существование. – М.: Наука, 1976. – 286 с. 2. Lotka A.J. Elements of Physical Biology. – Baltimore: Williams and Wilkins, 1925. 3. Николис Г., Пригожин И. Самоорганизация в неравновесных системах: от диссипативных структур к упорядоченности через флуктуации. – М.: Мир, 1979. – 512 с. 4. May R.M. Simple Mathematical Models with Very Complicated Dynamics // Nature. – 1976. – Vol. 261. – P. 459–467. 5. Goh B.S. Stability in models of mutualism // The American Naturalist. – 1979. – Vol. 113, № 2. – P. 261–274. 6. Lu Z., Takeuchi Y. Qualitative Stability and Global Stability for Lotka-Volterra Systems // J. of Mathematical ***ysis and Applications. – 1994. – Vol. 182, № 1. – P. 260–268. 7. Московкин В.М., Журавка А.В. Моделирование конкурентно-кооперационных взаимодействий: (контекст уравнений популяционной динамики в социально-экономических системах) // Бизнес Информ. – Харьков, 2002. – № 5–6. – С. 27–34. 8. Московкин В.М., Журавка А.В., Михайлов В.С. Расчет сценариев конкурентных, кооперационных и смешанных стратегий для n-мерной модели конкурентно-кооперационных взаимодействий в социально-экономических системах // Экономическая кибернетика. – Донецк, 2004. – № 5–6 (29–30). – С. 32–34. 9. Московкин В.М., Билаль Н.Е. Сулейман, Голиков Н.А. Математическая модель взаимодействия результатов различных видов НИОКР // Научно-техническая информация. Сер. 2. – 2011. – № 2. – С. 13–17.
Многомерная модель популяционной динамики Лотки-Вольтерра была предложена Вито Вольтерра в работе [1], но так как параллельно такого рода уравнения в биофизической и химической кинетике развивал А. Лотка [2], то за уравнениями популяционной динамики закрепились фамилии обоих ученых. К изучению данной модели обращались такие крупные ученые как Г. Николис и И. Пригожин [3], Р. Мэй [4] и др. При рассмотрении этой модели ученые, в основном, изучали хаpaктер устойчивости нетривиальной особой точки. Например, Б. Гох [5] при изучении моделей мутуализма показал, что необходимым и достаточным условием для локальной и глобальной устойчивости нетривиальной особой точки модели Лотки-Вольтерра является положительность всех ведущих (главных) миноров матрицы Якоби для этой модели. Позднее З. Лу и Е. Такеучи [6] доказали ряд теорем по глобальной устойчивости системы уравнений Лотки-Вольтерра. В работах по экономической динамике [7, 8] было замечено, что n-мерная система уравнений популяционной динамики Лотки-Вольтерра имеет 2n особых точек, но до сих пор доказательства этому представлено не было. Возможность использования таких уравнений в информационном анализе и моделировании взаимодействий результатов различных видов НИОКР показана в работе [9]. Исходная n-мерная модель Лотки-Вольтерра, на наш взгляд, может быть использована при моделировании конкурентных взаимодействий n научных фронтов в рамках широкой области научных исследований, при которых будут наблюдаться разнообразные варианты подавления одних научных фронтов другими, а также их сосуществования. Ниже будет сформулирована и доказана теорема о количестве и структуре особых точек n-мерной модели Лотки-Вольтерра.
Основная часть
Теорема. Количество особых точек n-мерной системы нелинейных обыкновенных дифференциальных уравнений Лотки-Вольтера с положительными коэффициентами и невырожденными случаями систем линейных алгебраических уравнений, возникающих при определении координат особых точек, равняется 2n, а их структура в отношении сочетания нулевых и ненулевых координат совпадает с биномиальными коэффициентами.
Доказательство. Будем рассматривать систему уравнений Лотки-Вольтера в виде
(1)
Для удобства доказательства теоремы перепишем правые части этой системы уравнений, приравненные к нулю, в виде:
(2)
Будем рассматривать невырожденные случаи решения линейных систем алгебраических уравнений, которые имеют единственные решения.
Из системы уравнений (2) сразу же выделяются две особые точки – нулевая и нетривиальная (ненулевая), которая является решением n-мерной системы линейных алгебраических уравнений, стоящих в скобках исходной системы (2). С точки зрения комбинаторной математики, этим особым точкам соответствуют следующие сочетания:
нулей из n переменных;
нулей из n переменных.
В первом случае мы имеем единственную нулевую особую точку, во втором – единственную ненулевую особую точку.
Далее, количество особых точек с сочетанием одной нулевой координаты из n переменных равняется , количество особых точек с сочетанием двух нулевых координат из n переменных равняется , количество особых точек с сочетанием i нулевых координат из n переменных равняется , количество особых точек с сочетанием (n – 1) нулевых координат из n переменных равняется . Следовательно, общее количество особых точек равняется
Таким образом, показано, что общее количество особых точек равняется 2n, а их структура в отношении сочетания нулевых и ненулевых координат повторяет последовательную совокупность коэффициентов в биноме Ньютона.
В этом доказательстве подразумевается следующее положение. Когда мы берем все особые точки с нулевыми координатами в количестве i, то оставшиеся системы линейных алгебраических уравнений (n – i)-порядка имеют единственные решения (невырожденные случаи).
Заключение
Для n-мерной системы уравнений популяционной динамики, предложенной в работах В. Вольтера и А. Лотки еще в середине 20-х годов прошлого века, до сих пор не была доказана теорема о количестве и структуре особых точек этой классической системы уравнений. В данной работе такая теорема была доказана с помощью элементарных методов комбинаторной математики и единственности решений систем линейных алгебраических уравнений для невырожденных случаев. С точки зрения информационного анализа и моделирования информационных процессов и систем, следует отметить, что динамическая система (1) может, в принципе, моделировать процесс конкурентных взаимодействий n научных фронтов в рамках широкой области научных исследований. Тогда в такой системе могут наблюдаться 2n вариантов исходов таких взаимодействий из которых 2n–2 будут связаны с подавлением одних научных фронтов другими, которые окажутся более конкурентоспособными.
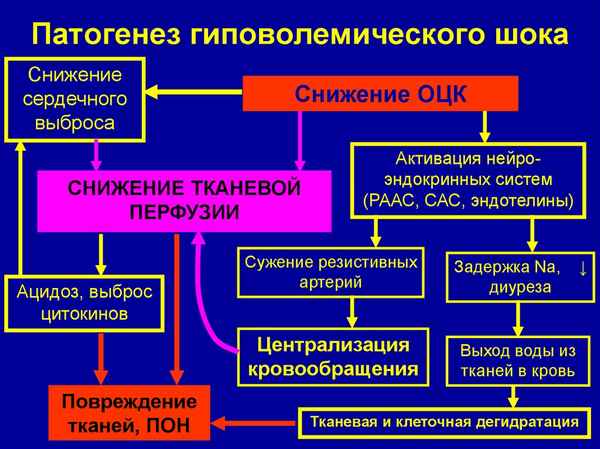Статья в формате PDF
138 KB...
25 04 2024 19:43:37
Статья в формате PDF
83 KB...
24 04 2024 19:38:24
Статья в формате PDF
255 KB...
23 04 2024 3:40:40
Статья в формате PDF
106 KB...
22 04 2024 6:19:58
Статья в формате PDF
114 KB...
21 04 2024 14:14:18
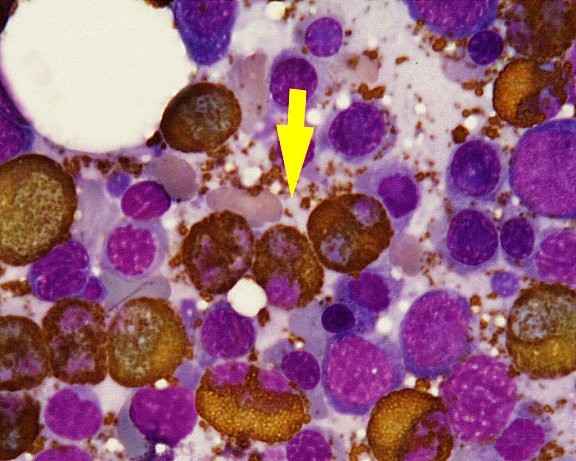Статья в формате PDF
107 KB...
20 04 2024 23:44:24
В настояще время весьма актуальной является задача поиска, отбора, поддержки и развития интеллектуально одарённых детей. «Трёхкольцевая модель одарённости» Рензулли включает следующие компоненты: высокий уровень интеллекта, креативность и усиленную мотивацию. Такие дети требуют дифференцированных учебных программ и особой педагогической поддержки. В современной пpaктике обучения используются педагогические стратегии и программы, которые предусматривают высокий уровень развития мыслительных процессов, совершенствование творческих способностей и быстрое усвоение знаний, умений и навыков. Процесс обучения одарённых детей требует создания особой образовательной среды. Ключевой фигурой в создании такой среды является учитель. Функция педагога состоит в сопровождении и поддержке, развитии личности ученика. Продуктивность взаимодействий обеспечивается включённостью ученика и учителя в общую целенаправленную деятельность.
...
19 04 2024 0:26:17
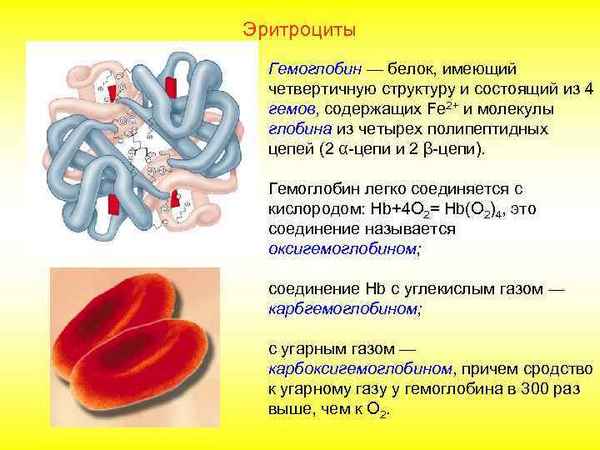В миниобзоре приведены сведения об основных результатах исследования эритроцитарных белков. Обсуждается строение и функции комплексов белка 4.1.R и белка 3 полосы, результаты исследованиябелков – трaнcпортеров, включая роль аквапорина 1 в трaнcпорте двуокиси углерода. Обсуждается представления о механизме Gárdos эффекта в эритроцитах. Приведены сведения об интеpaктоме белков цитозоля эритроцитов. Обсуждаются вопросы развития окислительного стресса в эритроцитах включая, роль белка пероксиредоксина 2. Показано участие гемоглобина в механизмах старения эритроцитов.
...
18 04 2024 18:48:31
Статья в формате PDF
321 KB...
17 04 2024 4:24:51
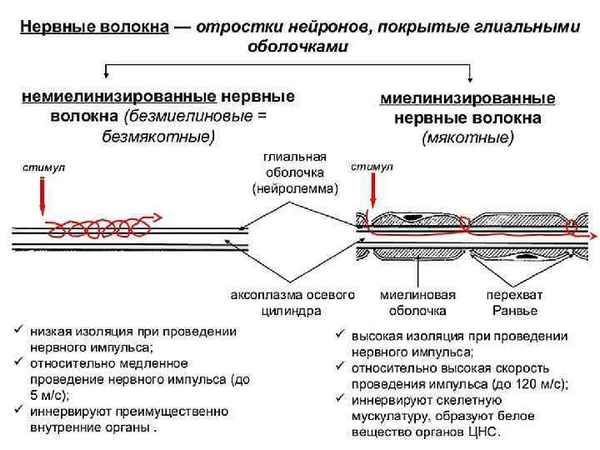Статья в формате PDF
113 KB...
16 04 2024 5:20:28
Статья в формате PDF
149 KB...
15 04 2024 16:24:20
Статья в формате PDF
113 KB...
14 04 2024 11:31:15
Статья в формате PDF
639 KB...
13 04 2024 3:42:17
Статья в формате PDF
267 KB...
12 04 2024 2:41:30
Статья в формате PDF
172 KB...
11 04 2024 14:42:40
Статья в формате PDF
277 KB...
10 04 2024 7:43:23
Статья в формате PDF
105 KB...
09 04 2024 5:42:36
Статья в формате PDF
135 KB...
08 04 2024 6:55:11
Статья в формате PDF
321 KB...
07 04 2024 5:30:46
Статья в формате PDF
311 KB...
06 04 2024 5:46:18
Статья в формате PDF
189 KB...
05 04 2024 9:29:12
Статья в формате PDF
329 KB...
03 04 2024 5:51:53
Статья в формате PDF
201 KB...
01 04 2024 13:46:24
Статья в формате PDF
321 KB...
31 03 2024 22:42:37
Статья в формате PDF
143 KB...
29 03 2024 11:47:29
Статья в формате PDF
108 KB...
28 03 2024 18:30:40
Статья в формате PDF
122 KB...
27 03 2024 9:53:42
Статья в формате PDF
224 KB...
26 03 2024 19:32:28
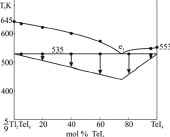Методами ДТА и РФА исследованы фазовые равновесия в системе Tl2S-Tl2Te-Tl9SbTe6 (А). Построены политермическое сечение Tl2S-Tl9SbTe6 и изотермическое сечение при 400К фазовой диаграммы, а также проекция поверхности ликвидуса системы А. Установлено, что она является квазитройным фрагментом четверной системы Tl-Sb-S-Te и хаpaктеризуется образованием широких областей твердых растворов на основе исходных соединений. Поверхность ликвидуса системы А состоит из трех полей, отвечающих первичной кристаллизации твердых растворов на основе соединений Tl2S, Tl2Te и Tl9SbTe6. В работе также обсуждены особенности фазовых равновесий в аналогичных системах и, в частности, показано, что все шесть систем данного типа хаpaктеризуются образованием твердых растворов на основе исходных соединений, причем наиболее широкие области гомогенности имеют соединения типа Tl9BVX6.
...
25 03 2024 23:23:34
Статья в формате PDF
349 KB...
24 03 2024 22:46:12
Статья в формате PDF
166 KB...
23 03 2024 10:28:30
Статья в формате PDF
124 KB...
22 03 2024 11:59:57
Статья в формате PDF
131 KB...
21 03 2024 0:21:23
Статья в формате PDF
121 KB...
20 03 2024 13:10:52
Статья в формате PDF
112 KB...
19 03 2024 7:33:12
Статья в формате PDF
283 KB...
17 03 2024 13:42:49
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
