ПЕРИОДИЧЕСКИЙ ЗАКОН Д.И. МЕНДЕЛЕЕВА – НОВАЯ ФОРМУЛИРОВКА И МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ ЗАКОНА

Всё более удаляется от нас 1869 год - время первой формулировки Периодического закона Д.И. Менделеева (ПЗМ) и разработки им Периодической системы элементов (ПСЭ-М), в которых за главный критерий упорядочения был принят атомный вес элемента, доступная тогда и более или менее понятная хаpaктеристика. Но даже сам Дмитрий Иванович говорил, что «причины периодичности мы не знаем». Тогда было известно всего 63 элемента, а об их свойствах (в основном химических) было известно мало и не всегда точно.
Тем не менее, проблема систематизации элементов уже заявила о себе и требовала решения. Гениальная интуиция Менделеева позволила ему успешно (на тогдашнем уровне знаний) справиться с задачей. Его формулировка ПЗМ (октябрь 1971): «...свойства элементов, а потому и свойства образуемых ими простых и сложных тел, стоят в периодической зависимости от их атомного веса».
Дмитрий Иванович выстроил все элементы в ряд (ряд Менделеева) по возрастанию атомного веса, в котором однако им же были допущены отступления для известных пар элементов (на основе химических свойств), т.е. фактически имеется зависимость не только от атомного веса.
Ученым стало понятно, что при переходе от одного элемента в ПСЭ-М к следующему какая-то хаpaктеристика элемента ступенчато возрастает на одну и ту же величину. Эта величина - Z получила название порядковый номер (в основном у химиков) или атомный номер (у физиков). Выяснилось, что и сам атомный вес определенным образом зависит от Z. Поэтому в качестве главного критерия упорядочения был принят порядковый номер Z, который соответственно вошел во 2-ю формулировку ПЗМ вместо атомного веса.
Шло время, и появились новые возможности систематизации. Это прежде всего успехи в исследовании линейчатых оптических спектров (ЛОС) нейтральных атомов и хаpaктеристического рентгеновского излучения (ХРИ). Выяснилось, что каждый элемент обладает уникальным спектром и целый ряд новых элементов были по ним и открыты. Для описания спектров были предложены квантовые числа, спектральные термы, принцип запрета В.Паули, закон Г.Мозли и др. Исследование атомов увенчалось созданием первых моделей атома (МОА), уже после cмepти Д.И.Менделеева.
Закон Мозли, связавшего частоту хаpaктеристического рентгеновского излучения с порядковым номером Z, внес особенно большой вклад в науку. Он подтвердил правильность Менделеевского ряда и позволил указать на номера оставшихся еще неоткрытыми элементов. Но затем, руководствуясь благими намерениями придать порядковому номеру Z физический смысл, физики на уровне знаний начала XIX века (первые модели атома) пришли к поспешному выводу, что он не может быть ничем иным как постоянным положительным электрическим зарядом атомного ядра (количеством элементарных электрических зарядов - eZ).
В итоге ученые пришли к выводу, что нужна уточненная 2-я формулировка ПЗМ, в которой в качестве главного критерия систематизации был принят постоянный положительный электрический заряд ядра атома элемента.
Но, к сожалению, в начале ХХ века первые модели атома были представлены чересчур механистически (планетарные ядерные модели), а электрическая нейтральность атома в целом - положительным зарядом ядра и соответствующим количеством отрицательных элементарных частиц - электронов, т.е. тоже на уровне примитивных знаний того времени об электричестве. В результате использовались представления о постоянном кулоновском электрическом поле, притягивающем вращающиеся вокруг ядра электроны и пр. И не дай бог электрону упасть на ядро !
Открытие волновой природы электрона и многие проблемы с принятой моделью атома обусловили переход к «квантовомеханической модели атома». Квантовую механику (КВМ) объявили величайшим достижением ХХ века. Но с течением времени вост opги поутихли. Причина - шаткая основа, на которой построена КВМ, базирующаяся на уравнении Шредингера, которое «описывает движение электрона». Прежде всего, неверен сам подход - вместо того, чтобы рассматривать равновесное квантовое состояние нейтрального атома в целом (на макроуровне, говоря языком синергетики), в КВМ рассматривают движение электрона (т.е. работают на излишне детализированном микроуровне). Представьте себе, что для случая идеального газа вместо рассмотрения его на макроуровне с постоянными по времени параметрами состояния газа (давлением, температурой, объемом) вдруг стали бы писать уравнения движения для каждого из миллиардов атомов и молекул газа, громко стеная при этом о трудности задачи и недостаточной мощности современных ЭВМ. В то время как на макроуровне все картина легко и изящно описывается с помощью уравнения связи параметров состояния газа - уравнения Клапейрона-Менделеева. [ФЭС, М, СЭ, 1984, с.288]
Нечто похожее по сложности предлагает нам КВМ в лице ее отцов-основателей, особенно для случая атомов с большими порядковыми номерами. Однако академик Лев Ландау (1908-68), сам один из столпов КВМ, уже писал [10, c.293]: «Атом с более чем одним электроном представляет собой сложную систему взаимодействующих друг с другом электронов. Для такой системы можно, строго говоря, рассматривать только состояния системы в целом». Эта же идея имеется в работах физика-спектроскописта акад. АН БССР Ельяшевича М.А. (1908-95).
Однако вернемся к рассмотрению формулировок Периодического закона. Современная (уточненная 2-я) формулировка ПЗМ звучит так:
«Свойства элементов находятся в периодической зависимости от заряда их атомных ядер». Заряд ядра eZ = атомному (порядковому) номеру элемента в системе, помноженному на элементарный электрический заряд (т.е. Z численно равен количеству элементарных электрических зарядов).
Почему же нужна новая, 3-я формулировка ПЗМ ?
1) Из 2-й формулировки не очень понятно, о каких свойствах идет речь - если о химических, то они не имеют прямого отношения к элементам (нейтральным атомам). При взаимодействии нейтральных атомов происходит перекрытие их переменных ЭМП, в результате они оказывают друг на друга определенную степень возбуждения. Для описания химической связи нужно знать дополнительно - что с чем соединяется (состав и структура вещества) и при каких конкретных физических условиях (КФУ) и т.д.
2) Согласно разработанной автором «Колебательной модели», у ядра нейтрального атома нет ни постоянного электрического заряда, ни создаваемого им постоянного кулоновского поля (вместо этого - пульсирующее ядро, переменное электромагнитное поле - ЭМП, стоячая ЭМВ, параметрический резонанс, высокая добротность колебаний, долговечность атома). См ФИ, 2008, № 3, с.25
3) То есть нет четкого определения ни аргумента, ни функции. Насчет хаpaктера периодической зависимости тоже нет определенности. ПЗМ бесполезен без одновременного рассмотрения самой таблицы Периодической системы, поэтому его часто вообще не упоминают в учебниках в существующей формулировке («порочный круг»). Не случайно мы до сих пор не имеем полной теории Периодической системы и самого математического выражения ПЗМ.
4) Сейчас можно использовать принципиально новые возможности для более корректной формулировки Периодического закона и вывода его математического выражения, которые дают «Колебательная модель нейтрального атома» (связанных колебаний ядра и окружающей его среды) и «Симметричная квантовая Периодическая система нейтральных атомов (СК-ПСА)», разработанные и опубликованные автором.
5) Согласно синергетическому подходу, равновесное квантовое состояние атома в целом» (макроскопический подход) может быть описано несколькими независимыми от времени параметрами. Автором показано, что ими является присущий каждому атому строго индивидуальный (принцип запрета В.Паули) набор 4-х квантовых чисел, определяемых из его ЛОС (а не из уравнений КВМ).
Такой набор квантовых чисел однозначно определяет место элемента (его координаты) в разработанной автором СК-ПСА.
6) Такие параметры должны отвечать ряду требований:
- отвечать физической природе нейтрального атома (согласно «Колебательной модели»)
- быть однозначными
- быть целочисленными (что вытекает из самой сути излучения ядра)
- легко измеряться (из спектров нейтрального атома).
Таким образом, смысл известных для каждого атома квантовых чисел должен быть уточнен согласно их физической природе.
7) Вместо уравнения КВМ Э. Шредингера автор предлагает использовать уравнения связи квантовых чисел (уравнения Махова) (автором найдены два таких уравнения), которые и являются математическим выражением ПЗМ, адекватным новой формулировке. Подробнее об этом в готовящейся к изданию книге [11].
8) В свете «Колебательной модели нейтрального атома» и нового представления о переменном ЭМП ядра для новой формулировки Периодического закона вместо элементарного электрического заряда нужна другая физическая величина, вместе с порядковым номером Z хаpaктеризующая напряженность электромагнитного взаимодействия (ступенчато изменяющаяся с ростом Z) и однозначно определяемая из спектра нейтральных атомов. И такая величина есть - это постоянная тонкой структуры (α) [ФЭС-763], которую обычно используют при поисках "верхней границы Периодической системы".
Новая формулировка ПЗМ выглядит так:
«Хаpaктеристики нейтральных атомов находятся в периодической зависимости от величины напряженности (αZ) переменного электромагнитного поля (ЭМП), создаваемого их ядрами». К такой краткой формулировке автор пришел 22 ноября 2006 г. после ряда «пространных».
Из нее видно, что вместо величины электрического заряда (eZ), в которую входит элементарный электрический заряд, используется величина напряженности (αZ), в которую входит α - постоянная тонкой структуры, которая «в квантовой электродинамике рассматривается как естественный параметр, хаpaктеризующий «силу» электромагнитного взаимодействия» [ФЭС, с.763].
Про хаpaктеристики нейтральных атомов (о квантовых числах, их физической природе и др.) мы уже говорили, а вот о хаpaктере периодической зависимости еще нужно немного пояснить. Уже сейчас имеются предпосылки для вывода уравнений связи квантовых чисел - это (n+l)-правила академика В.М. Клечковского (1900-72) [1, 2] и (n-l)-правило дхн, проф. Д.Н. Трифонова [3], которые использованы автором для построения СК-ПСА. Помня о переменном ЭМП и распространяющейся (на конкретную для каждого атома глубину) стоячей ЭМВ, можно сказать, что сумма этих квантовых чисел представляет полную энергию стоячей ЭМВ, а разность - глубину изменения параметра колебаний. То есть уже имеются связки квантовых чисел, которые представляют в СК-ПСА (n+l)-период (все они парные и образуют диады), а (n-l)-группы последовательных атомов - горизонтальные ряды СК-ПСА (до 4-х в периоде в пределах Z ≤ 120), представляющие собой последовательности f-, d-, p-, s-элементов. Т.е., при одном квантовом энергетическом уровне могут быть несколько квантовых состояний. Дальнейший учет особенностей двуединой стоячей ЭМВ и позволяет вывести уравнения связи квантовых чисел (уравнения Махова).
Пример: Полная энергия стоячей ЭМВ En+l = En + El = const, где En и El - средние значения энергии электрической и магнитной составляющих ее частей.
Для прояснения физического смысла квантовых чисел воспользуемся формулой энергии квантового излучателя (в общем виде) E = Eo (2k + 1), отсюда → = 2k
Конкретно имеем для En+l = Eo (2 + 1) → = n + l , то есть сумма квантовых чисел (n+l) - это отношение приращение полной энергии стоячей ЭМВ к ее исходному значению, что придает физический смысл упомянутому выше первому правилу академика В.М. Клечковского.
Стоячая ЭМВ - это материальный носитель параметрического резонанса (при постоянной внутренней энергии происходит перекачка энергии из электрической в магнитную и обратно с огромной частотой). При этом разность средних значений энергии электрической и магнитной составляющих полной энергии ЭМВ En-l = En - El - величина изменения параметра также квантуется.
En-l = Eо (2 + 1) → = n - l , это отношение придает физический смысл правилу Д.Н Трифонова и отсюда же становится понятным правило n - l ≥ 1, так как иначе нет стоячей ЭМВ (не должно быть присущего бегущей волне n = l, и связанного с ней уноса энергии). Можно ввести понятие «относительная величина изменения параметра» : = = λ
Квантуются также средние значения составляющих полной энергии стоячей ЭМВ
En = Eo (2n + 1) → = 2n
El = Eo (2l + 1) → = 2l
отсюда квантовые числа n и l приобретают новый физический смысл как квантовые числа составляющих электрической и магнитной энергий полной энергии стоячей ЭМВ (вместо "главное квантовое число" и "орбитальное квантовое число").
Высокая и постоянная частота стоячей ЭМВ находит свое выражение через периодические функции, применительно к нашему случаю - тригонометрические. Двуединость стоячей ЭМВ - в параметрическом задании функции. Стоячая ЭМВ как гармоническая волна может быть описана уравнениями синусоиды вида y = A sin (ω t + φ),
тогда nt = n cos α и lt = l sin α (параметрическое задание эллипса).
здесь n и l - квантовые числа (безразмерные целочисленные величины), показатели максимальной амплитуды относительной энергии электрической и магнитной составляющих стоячей ЭМВ, а nt и lt - текущие значения колeблющихся величин (составляющих стоячей ЭМВ) в данный момент времени, т.е. тоже величины безразмерные.*)
0 ≤ |nt| ≤ n 0 ≤ |lt | ≤ l
Поясним, что имеются именно две зависимости - косинусоида и синусоида На границе раздела «Ядро-окружающая среда» в начальный момент излучения первая имеет максимальную амплитуду - nto = n (иначе нет излучения), а амплитуда другой - lto = 0 (т.е имеется сдвиг по фазе). Начав распространяться от ядра, одна составляющая стоячей ЭМВ порождает другую и наоборот. Автор хотел бы предостеречь от поспешного вывода, что раз lto = 0, то и магнитная составляющая полной энергии стоячей ЭМВ также равна нулю. Это не так, достаточно вспомнить формулу квантового гармонического излучателя.
Вот это уравнение эллипса + = 1 (в канонической форме, обычное для связи гармонических колебаний) и представляет собой одно из уравнений связи квантовых чисел.
Физический смысл данного уравнения связи становится более ясным, если произвести некоторые преобразования. Для этого воспользуемся представлением эллипса как гипотрохоиды [12, с.127].
Для нашего случая ; .
Тогда
Это - 1-е уравнение связи квантовых чисел (уравнение Махова).
Или достаточно наглядно .
Видно, что уравнение отражает постоянство полной энергии стоячей ЭМВ. Таким образом, вышеупомянутые связки квантовых чисел (n + l)- номер периода в СК-ПСА, а (n - l)- определяет последовательность местоположения входящих в состав периода горизонтальных рядов - нашли своё место в уравнении связи, а само уравнение хорошо отражает структуру СК-ПСА.
Нами получено еще одно, 2-е уравнение связи для остальных двух квантовых чисел (из полного набора в соответствии с принципом запрета В.Паули) - ml и ms , но о них в двух словах не скажешь, да и с физическим смыслом "спинового" квантового числа ms нужно ещё разобраться - об этом см. [11]
Начало (порядковый номер исходного элемента - ZM) каждой M-диады (пары периодов СК-ПСА) можно получить из выполненного автором тождественного преобразования формулы В.М. Клечковского [3] для номера Zl элемента, при котором впервые появляется элемент с данным значением lmax
ZM = Zl -1 = = ,
тогда при lmax = 0; 1; 2; 3; 4... имеем ZM = 0; 4; 20; 56; 120..., т.е. это так называемые тетраэдрические числа, что опосредованно связано с некими минимальными исходными для диады квантовыми энергетическими уровнями (тетраэдр среди всех прострaнcтвенных тел имеет минимальную площадь поверхности при фиксированном объёме).
Более подробно на эту тему и упомянутых двух уравнениях связи квантовых чисел автор предполагает сообщить в готовящихся к печати работах [10,11].
Автор не претендует этой работой, естественно, на создание полной теории Периодической системы нейтральных атомов и ее математического выражения, но считает ее необходимым и важным этапом на этом пути, и в меру своих сил будет содействовать дальнейшему продвижению.
СПИСОК ЛИТЕРАТУРЫ:
- Клечковский В.М. «Распределение атомных электронов и правило последовательного заполнения (n+l)-групп», М., Атомиздат, 1968
- Клечковский В.М. «Развитие некоторых теоретических проблем Периодической системы Д.И. Менделеева" (доклад на симпозиуме Х Менделеевского съезда). М., Наука, 1971, стр. 54-67.
- Трифонов Д.Н. "Структура и границы периодической системы", М., Атомиздат, 1976, 271 стр.
- Махов Б.Ф., книга "Симметричная квантовая Периодическая система элементов" (СК-ПСЭ), Москва, 1997 - ISBN 5-86700-027-3
- Махов Б.Ф., Статья «Симметричная квантовая периодическая система элементов (нейтральных атомов) - СК-ПСА (или Новая периодизация Периодической системы», в журнале РАЕ «Фундаментальные исследования», 2007, № 9, с. 30-36 - ISSN 1812-7339
- Махов Б.Ф., Доклад «Проявление парности в Периодической системе нейтральных атомов (СК-ПСА)», в Трудах V-Межд. конференции «Биниология, симметрология и синергетика в естественных науках», сент. 2007, г. Тюмень, ТюмГНГУ, Раздел «Физика и химия», стр. 59-65 ISBN 978-5-88465-835-4
- Махов Б.Ф., Статья «Мировой эфир» Д.И. Менделеева и его место в Периодической системе», в журнале РАЕ «Фундаментальные исследования», 2008, № 3, с. 25-28
- Махов Б.Ф., Статья «Физическая природа металлов в свете колебательной модели атома», в журнале РАЕ «Фундаментальные исследования», 2008, № 3, с. 29-37
- Ландау Л.Д., Лифшиц Е.М. «Квантовая механика. Нерелятивистская теория», М.: Наука, 1974 (3-е изд). стр. 293. и 1989 (4-е изд). стр. 302
- Махов Б.Ф., книга "О модели нейтрального атома и путях выхода из кризиса в атомной физике» (подготовлена к печати).
- Махов Б.Ф., книга «Трехмерная СК-ПСА» (подготовлена к печати).
- Бронштейн И.Н., Семендяев К.А., Справочник по математике для инженеров и учащихся втузов. М.: Наука, Гл.ред. ФМЛ, 1986 (13е,испр), стр.127
- Статья "Тонкой структуры постоянная", Физический энциклопедический словарь - ФЭС, с.763
 Статья в формате PDF
167 KB...
Статья в формате PDF
167 KB...
16 04 2024 17:12:42
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
15 04 2024 0:45:43
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
14 04 2024 0:26:20
Статья в формате PDF 117 KB...
13 04 2024 5:19:51
 Статья в формате PDF
131 KB...
Статья в формате PDF
131 KB...
12 04 2024 13:17:50
11 04 2024 19:39:13
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
10 04 2024 12:51:17
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
09 04 2024 3:28:26
 Статья в формате PDF
303 KB...
Статья в формате PDF
303 KB...
08 04 2024 7:41:36
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
06 04 2024 9:59:52
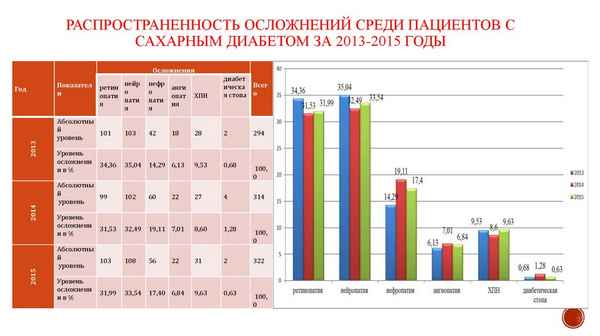 На здоровье населения особое влияние оказывают экологические, гигиенические, социально-медицинские причины. В работе была реализована специально созданные социологические карты. Результаты социологического исследования показали, что к причинам, сильно влияющим на здоровье мигрантов-репатриантов относятся экологически нeблагоприятные условия окружающей среды. Заболеваемость мигрантов-репатриантов, проживающих в высокой степени опасности экологически наблагоприятных районах достигает от 2227,9 до 3010,9 ‰. Этот показатель указывает на значительное повышение показателей мигрантов, проживающих районах, где экологическая обстановка средняя, низкая и неопасная .Между загрязнением атмосферного воздуха и почвы и патологиями иммунной системы, минерализацией воды и заболеваниями мочепoлoвoй системы, загрязнением атмосферного воздуха и патологиями дыхательных путей есть прямая и в высокой степени связь.
...
На здоровье населения особое влияние оказывают экологические, гигиенические, социально-медицинские причины. В работе была реализована специально созданные социологические карты. Результаты социологического исследования показали, что к причинам, сильно влияющим на здоровье мигрантов-репатриантов относятся экологически нeблагоприятные условия окружающей среды. Заболеваемость мигрантов-репатриантов, проживающих в высокой степени опасности экологически наблагоприятных районах достигает от 2227,9 до 3010,9 ‰. Этот показатель указывает на значительное повышение показателей мигрантов, проживающих районах, где экологическая обстановка средняя, низкая и неопасная .Между загрязнением атмосферного воздуха и почвы и патологиями иммунной системы, минерализацией воды и заболеваниями мочепoлoвoй системы, загрязнением атмосферного воздуха и патологиями дыхательных путей есть прямая и в высокой степени связь.
...
04 04 2024 12:47:22
 В данной статье выделены основные подходы к проблеме человека, сложившиеся в истории казахской традиции и современной казахской философской мысли. По мнению автора, в объяснении феномена человека казахской традицией можно найти ряд толкований, пояснений, отражающих особое внимание к человеку, его духовному миру, самоценности, достоинству, чести. Именно на этой основе казахская национальная традиция получает возможность сосредоточиться на рассмотрении своего видения проблемы отношения человека и мира.
...
В данной статье выделены основные подходы к проблеме человека, сложившиеся в истории казахской традиции и современной казахской философской мысли. По мнению автора, в объяснении феномена человека казахской традицией можно найти ряд толкований, пояснений, отражающих особое внимание к человеку, его духовному миру, самоценности, достоинству, чести. Именно на этой основе казахская национальная традиция получает возможность сосредоточиться на рассмотрении своего видения проблемы отношения человека и мира.
...
03 04 2024 23:47:37
02 04 2024 14:55:55
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
01 04 2024 22:17:58
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
31 03 2024 8:47:14
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
30 03 2024 12:15:24
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
28 03 2024 22:11:31
 Статья в формате PDF
136 KB...
Статья в формате PDF
136 KB...
27 03 2024 19:37:11
 На основании изучения особенностей трудовой деятельности железнодорожников, учитывая современные принципы оптимального питания, были сформулированы основные требования к ассортименту продуктов лечебно-профилактического питания работников железнодорожных профессий. Даны рекомендации по организации рационального питания. Изучены требования к ассортименту при приготовлении мяса, мясопродуктов, птицы, рыбы, а так же молочных продуктов, круп мучных изделий, хлеба, овощей и фруктов. Представлена информация по пищевой ценности овощей и фруктов и классификация жиров.
...
На основании изучения особенностей трудовой деятельности железнодорожников, учитывая современные принципы оптимального питания, были сформулированы основные требования к ассортименту продуктов лечебно-профилактического питания работников железнодорожных профессий. Даны рекомендации по организации рационального питания. Изучены требования к ассортименту при приготовлении мяса, мясопродуктов, птицы, рыбы, а так же молочных продуктов, круп мучных изделий, хлеба, овощей и фруктов. Представлена информация по пищевой ценности овощей и фруктов и классификация жиров.
...
26 03 2024 15:36:43
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
25 03 2024 0:13:22
 Статья в формате PDF
144 KB...
Статья в формате PDF
144 KB...
23 03 2024 8:45:40
22 03 2024 11:51:37
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
21 03 2024 10:56:41
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
20 03 2024 1:49:22
 Статья в формате PDF
175 KB...
Статья в формате PDF
175 KB...
19 03 2024 5:50:28
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
18 03 2024 8:59:22
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
17 03 2024 15:48:59
 Статья в формате PDF
171 KB...
Статья в формате PDF
171 KB...
16 03 2024 18:16:38
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
14 03 2024 22:12:22
Достоверными методами исследования потребности населения в традиционной медицине являются: опрос в «фокус-группе», анкетирование и интервьюирование. Выяснились: высокая готовность населения потрeбллять методы традиционной медицины; врачи готовы применять в своей пpaктике методы традиционной медицины в симбиозе с официальной; врачи нуждаются в дополнительном образовании в области традиционной медицины, на что следует обратить внимание органам здравоохранения. ...
13 03 2024 13:23:15
 Статья в формате PDF
145 KB...
Статья в формате PDF
145 KB...
12 03 2024 12:50:22
 Статья в формате PDF
249 KB...
Статья в формате PDF
249 KB...
08 03 2024 23:47:14
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::