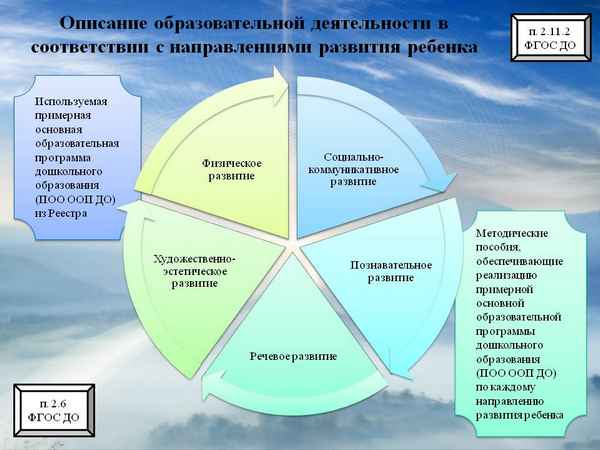
О МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИЕ НЕЛИНЕЙНЫХ ВОЛНОВЫХ ПРОЦЕССОВ

1. В работе даются модели, порождающие нелинейные и (или) сильно нелинейные волн в струнах и других одномерных объектах.
Нелинейные волновые процессы обычно моделируются при помощи нелинейных дифференциальных уравнениях в частных производных. Для нелинейных аналогов волнового уравнения имеем [1]:
utt - с2uxx=h(u,ut,ux,t,x), (1)
где h - нелинейная функция, структура которой определяется геометрическими и (или) физическими особенностями задачи. Раскладывая функцию h в ряд, в разных приближениях можно получать модели нелинейных волновых процессов.
Нелинейные волновые эффекты многочисленны и многообразны. Показывается, что при рассмотрении простейших нелинейных моделей проявляются такие весьма хаpaктерные и важные явления как «деформирование» и «опрокидывание» профилей волн [1].
Весьма важной моделью нелинейных волн служит нелинейное уравнение Клейна-Гордона:
utt - с2uxx=Ф(u), (2)
где Ф(u) - некоторая гладкая или разрывная функция, описывающая распределенные нелинейные восстанавливающие силы. Влинейном приближении Ф(u)=-ku (k>0) имеем известную модель струны «на упругой постели».
2. Весьма важную модель - модель нелинейной струны можно получить, учитывая в представлении для упругой энергии системы в первом приближении члeн, кубический по смещению [1]. Ограничиваясь рассмотрением достаточно длинных волн, можно получить дополнительные члeны уравнения движения, зависящие лишь от деформации ux , но не от ее производных. Кроме того, в первом приближении можно записать можно записать также и члeн, учитывающий дисперсию. Тогда уравнение нелинейной струны (или уравнение продольных колебаний нелинейного стержня) можно привести к виду [1]:
utt - с2(uxx+l2u4x - buxuxx )=0, (3)
где c - по-прежнему скорость распространения волн в линейной модели, l - масштабный, считающийся малым, b - также малый параметр, хаpaктеризующий интенсивность нелинейных сил. Выбор положительного знака перед l2 соответствует предположению, что среда имеет отрицательную дисперсию и групповая скорость убывает с ростом волнового числа. Дисперсия в данной модели оказывается нормальной. Выбор противоположенного знака привел бы к модели, аналогичной известной модели балки Бернулли [1].
Если Ф(u) - суть сингулярная обобщенная функция описывающая условия удара, то приходим к нелинейному уравнению Клейна-Гордона, моделирующее виброударную систему с паспределенными ударными элементами. [2]..
3. Весьма интересную базовую модель дает называемое уравнение Кортевега - де Фриза, (уравнение КдФ) оказывающееся принципиальным при рассмотрении моделей нелинейных волн [1].
wt + wx+εwxxx +μwwx =0. (4)
Если перейти к подвижной системе координат x→x-t, то вместо (4) получим
wt +μwwx +εwxxx =0. (5)
Данное уравнение также называют уравнением Кортевега - де Фриза. При замене w→ - w вместо (.14) будем иметь:
wt + wx+εwxxx -μwwx =0. (6)
Если продифференцировать это уравнение по t и заменить значение wt его представлением из (6), то:
wtt - wxx- 2εw4x + 2μ(wwx)x+εμ(2wwxx+0,5wx2)хх - ε2 w6x -μ2(w2wx)x = 0, (7)
то есть (3) и (7) совпадают с точностью до члeнов ~ε2 и ~μ2 . Следовательно, решения уравнения КдФ (6) точно удовлетворяют уточненному уравнению нелинейной струны (7) и приближенно исходному уравнению (3). О других примерах волновых уравнений, множество решений которого содержит решения уравнения КдФ см. например в [1].
Работа выполнена при поддержке РФФИ (проект № 04-01-00611).
СПИСОК ЛИТЕРАТУРЫ:
- Уизем Дж. Линейные и нелинейные волны.- М.: Наука-1997. - 622 с.
- Крупенин В.Л. К описанию динамических эффектов, сопровождающих колебания струн вблизи однотавровых ограничителей// ДАН. - . 2003,. № 388 (3).- С.12-15.
 Статья в формате PDF
259 KB...
Статья в формате PDF
259 KB...
15 04 2024 18:35:15
14 04 2024 13:22:37
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
13 04 2024 17:24:43
 Статья в формате PDF
429 KB...
Статья в формате PDF
429 KB...
12 04 2024 21:40:13
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
11 04 2024 14:23:47
 Статья в формате PDF
136 KB...
Статья в формате PDF
136 KB...
10 04 2024 11:19:31
09 04 2024 16:47:16
 Статья в формате PDF
366 KB...
Статья в формате PDF
366 KB...
08 04 2024 17:31:45
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
06 04 2024 4:21:34
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
04 04 2024 22:20:54
 Статья в формате PDF
174 KB...
Статья в формате PDF
174 KB...
03 04 2024 19:12:24
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
02 04 2024 6:57:36
01 04 2024 10:40:23
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
31 03 2024 14:58:35
 Статья в формате PDF
199 KB...
Статья в формате PDF
199 KB...
30 03 2024 16:37:12
 Статья в формате PDF
267 KB...
Статья в формате PDF
267 KB...
29 03 2024 5:37:28
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
28 03 2024 13:42:40
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
27 03 2024 23:14:59
 Статья в формате PDF
266 KB...
Статья в формате PDF
266 KB...
26 03 2024 7:37:32
 Статья в формате PDF
251 KB...
Статья в формате PDF
251 KB...
25 03 2024 3:33:30
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
24 03 2024 13:44:39
 Статья в формате PDF
130 KB...
Статья в формате PDF
130 KB...
22 03 2024 23:34:21
 Статья в формате PDF
264 KB...
Статья в формате PDF
264 KB...
21 03 2024 13:18:17
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
20 03 2024 0:27:40
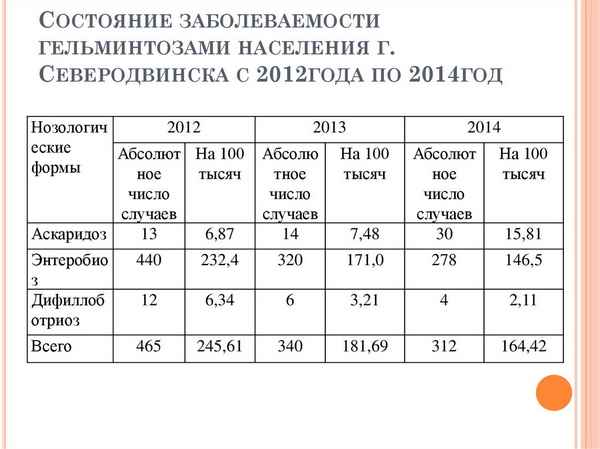 Статья в формате PDF
143 KB...
Статья в формате PDF
143 KB...
19 03 2024 1:17:15
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
18 03 2024 4:24:27
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
17 03 2024 23:38:28
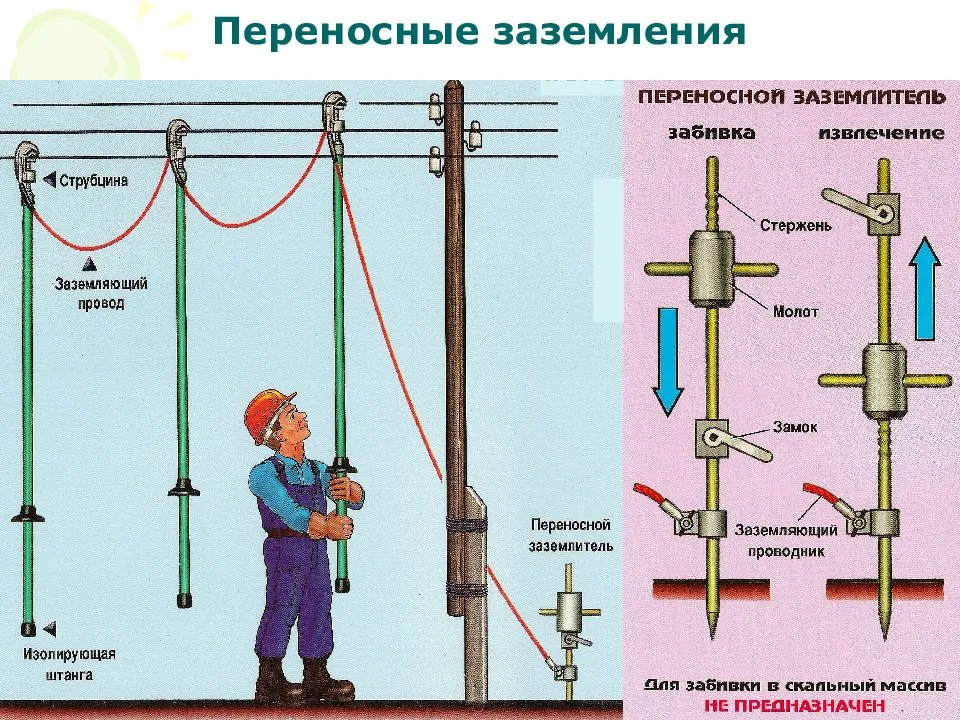 Статья в формате PDF
285 KB...
Статья в формате PDF
285 KB...
16 03 2024 17:59:28
 Статья в формате PDF
207 KB...
Статья в формате PDF
207 KB...
15 03 2024 20:19:16
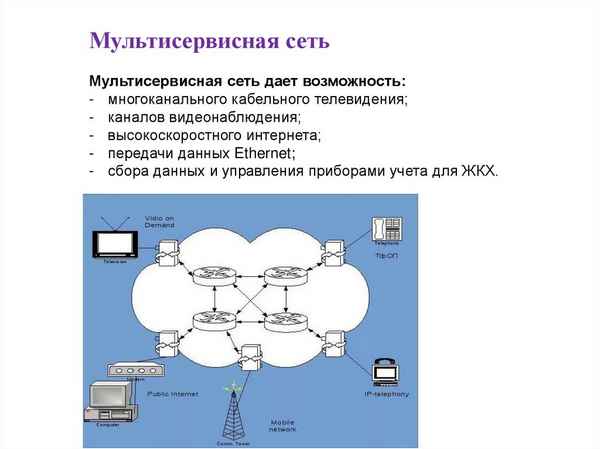 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
14 03 2024 12:43:23
 Изложены ключевые положения главных системных концепций современного естествознания — системологии (общей теория систем) и синергетики (теории самоорганизующихся систем). Рассмотрены основные свойства системных объектов: дискретность, элемент, связи, структура, паттерн, организация, целостность, интеграция, иерархия, управление, самоорганизация. Охаpaктеризованы особенности биологических систем: обмен веществ, итеративность, дискретность (прострaнcтвенная и временная), избыток структурных элементов и связей между ними, наследственность и изменчивость, способность к самоорганизации и саморазвитию, раздражимость и возбудимость, способность к адаптации, самовоспроизведение (размножение).
...
Изложены ключевые положения главных системных концепций современного естествознания — системологии (общей теория систем) и синергетики (теории самоорганизующихся систем). Рассмотрены основные свойства системных объектов: дискретность, элемент, связи, структура, паттерн, организация, целостность, интеграция, иерархия, управление, самоорганизация. Охаpaктеризованы особенности биологических систем: обмен веществ, итеративность, дискретность (прострaнcтвенная и временная), избыток структурных элементов и связей между ними, наследственность и изменчивость, способность к самоорганизации и саморазвитию, раздражимость и возбудимость, способность к адаптации, самовоспроизведение (размножение).
...
13 03 2024 9:39:31
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
12 03 2024 3:52:50
11 03 2024 3:42:21
 Статья в формате PDF
288 KB...
Статья в формате PDF
288 KB...
10 03 2024 5:13:25
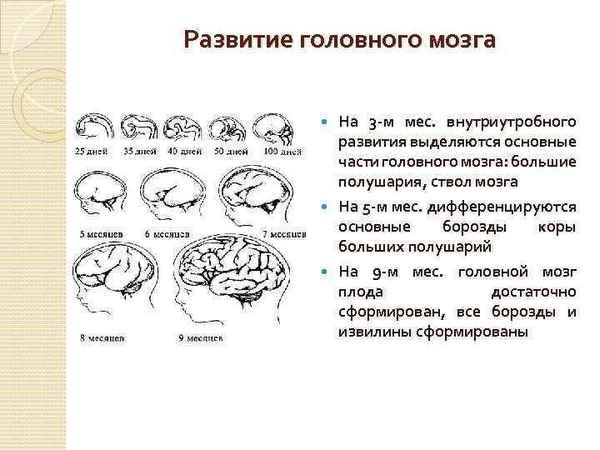 В статье на основании анализа серий срезов зародышей человека изучены особенности формирования артериального русла отделов головного мозга, определены возрастные критерии появления закладок как отделов головного мозга, так и основных сосудов и их ветвей в плане обоснования возможных вариантов строения артериальной сети головного мозга в онтогенезе.
...
В статье на основании анализа серий срезов зародышей человека изучены особенности формирования артериального русла отделов головного мозга, определены возрастные критерии появления закладок как отделов головного мозга, так и основных сосудов и их ветвей в плане обоснования возможных вариантов строения артериальной сети головного мозга в онтогенезе.
...
09 03 2024 12:35:13
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
08 03 2024 17:33:32
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::