УРАВНЕНИЯ ДЛЯ КООРДИНАЦИОННОГО ЧИСЛА В НЕУПОРЯДОЧЕНЫХ СИСТЕМАХ

Наш приближенный метод основан на использовании рекуррентного уравнения для фазовых, топологических переходов вещества, полученного при математическом описании аэро и гидродинамики зернистого слоя в точках псевдоожижения - кипения в зависимости от порозрости неподвижного слоя. Это уравнение имеет вид [2]:
где η1,η - плотность упаковки частиц в псевдофазах, в близи (до и после) топологического перехода, К - гидродинамический параметр проницаемости слоя, так называемая "константа" Козени - Кармана:
Покажем, что знаменатель в скобках выражения (1) представляет собой координационное число для невзаимодействующих частиц со случайной упаковкой в слое. Преобразуем уравнение (1) для точки ФТП типа "жидкость газ", "твердая дисперсная фаза газ", "псевдожидкая фаза -газ" при критическом состоянии вещества к виду:
V - V1 = V / 3ln(2K)
где V, V1 - объем менее плотной и более плотной фазы в точке ФТП
Подставляя правую часть этого выражения в уравнение Менделеева-Клапейрона-Клаузиуса, получим:
где Т, q - температура и скрытая теплота ФТП.
Преобразуем это выражение к виду полагая что для псевдоожиженного слоя невзаимодействующих частиц в точке ФТП (в точке псевдоожижения - кипения слоя) выполняется равенство идеальных газов РV=RT, где параметры Р и V могут быть определены давлением псевдоожижающего агента и объемом псевдоожиженного слоя:
Интегрирование этого выражения в предположении, что скрытая теплота фазотопологического перехода q не зависит от температуры, дает
Преобразуем это выражение к виду
Выражение в скобках левой части этого равенства примем за коэффициент Z для конденсированной фазы (псевдотвердой, жидкой и псевдожидкой), а при критическом состоянии вещества он представляет собой критический коэффициент, равный по величине координационному числу атомов в плотной фазе флуктуаций плотности (в псевдожидкой фазе) ZC = RTC / PCVC.Следовательно коэффициент Z в точке ФТП представляет собой координационное число атомов (частиц) в псевдоконденсированной фазе, где RT≠ РV, тогда как в псевдоожиженной системе невзаимодействующих частиц RT=PV. В результате принятых соображений, получим
ZPVlnP = -3qln(2K)±cRT
либо
ZRTlnP = -3qln(2K)±cRT (2)
Пологая, что q = ±RTlnP и пренебрегая постоянной интегрирования (с=0) для невзаимодействующих частиц монодисперсного слоя и элементов структуры конденсированной фазы, получим:
Z = 3ln (120,754· з51) (3)
где η1 - плотность упаковки элементов структуры в более плотной фазе в точке ФТП.
Из этого уравнения при з1 ≥0,4098 ≥Z 1 , что указывает на невозможность существования в природе жидкой конденсированной фазы с плотностью упаковки з1 < 0,4098 невзаимодействующих элементов ее структуры со случайной их упаковкой (т.е. с топологическим беспорядком), а при з1 ≥0,38337 ≥Z0 для газовой фазы. Величина ZСК =120,754з51 представляет собою число элементов (частиц) в скоплении вместе с центральным. Выражение (3) можно записать в общем виде с учетом силовой константы их взаимодействия k:
Z = kln (120,754· з51), где k =3...4 (4)
Из этого уравнения для невзаимодействующих (k≤ 3) и взаимодействующих элементов структуры (k ≤4) соответственно в псевдожидкой фазе при з1=0,6403...0,6655 получим Z =7,69...8,27 и Z=10,3...11,0 . Величина η=0,6655 получена из уравнения (1) при η1=0,74048. Полагая, что для критического состояния вещества q=-RCTClnPC/3 из выражения (2) получим:
ZС = kСln (120,754· з5ж), (5)
где Ж - плотность упаковки атомов в плотной фазе флуктуаций плотности, которая незначительно отличается от величины ее в жидкой фазе при температуре кипения (плавления) вещества.
Для конденсированной жидкой фазы в точке кипения (плавления) вещества и в критической точке выражение (5) можно записать в общем виде:
где с - константа взаимодействия атомов в жидкой фазе, с ≤1. Так как при ηж=0,6403...0,6038...0,5255 и с=1 из выражения (6) Zс=4...3,76...3,0; при с=3 Z=12...11,3...9, а при с=2,549 Zс=10,2...9,6...7,65.
Для уравнения (5) определим изменение величины kс в пределах изменения 3 ≤ Z ≤ 4 . Для этого воспользуемся наименьшем значением координационного числа ZC =10зC = 2,549 для невзаимодействующих элементов псевдофазы:
Коэффициент kс=1,1769 приведем к кратному значению на одно из десяти возможных чисел в первой, во второй и в последующих сферах ближайшего окружения центральной частицы в трехмерном прострaнcтве с увеличением их числа при разрыхлении структуры:
Из этого выражения при ηж≤0,6403 получим широкий спектр стандартных значений Zс, при четных значениях показателя степени n:Zc=2,65…2,74…2,82…2,92…3,02…3,12…3,22…3,33…3,44…3,55…3,67…3,79…3,92…4,05…4,18…, а при η1≤0,6038 – Zc=2,67…2,76…2,85…2,95…3,04…3,15…3,25…3,36…3,47…3,58…3,70…3,82…3,95…4,08…4,2….
Следовательно с уменьшением плотности упаковки частиц в псевдожидкой фазе коэффициент kс понижается, при этом возрастает число частиц в первой сфере ближайшего окружения. При n=10 эти ряды начинаются величинами Zc=3 и Zc=2,67 соответственно.
Коэффициент kс=1,5692 приведем к кратному значению на одно из двенадцати возможных чисел ближайшего окружения центрального атома в трехмерном прострaнcтве с увеличением их числа при разрыхлении структуры:
где n≥0…12 – ряд чисел ближайшего окружения центрального атома в флуктуациях плотности. Из этого выражения при ηж≤0,6403 получим: Zc=2,663…2,765…2,870…2,980… 3,094…3,213…3,335…3,463…3,596…3,733…3,87 6…4,024, а при ηж=0,6038- Zc=2,36…2,45…2,54…2,64…2,75…2,85…2,95…3,07…3,18…3,30…3,43…3,56…3,70 …3,85…3,99…4,14. При n≥6 эти ряды начинаются величинами Zc=3,2 и Zc=2,85 соответственно, а при n=12 Zc=4 и Zc=3,56. При Z=10, что хаpaктерно для большинства жидких металлов, это выражение имеет вид:
Если плотность упаковки атомов определяется в жидкой фазе при температуре кипения (плавления) вещества, то в полученные результаты укладываются все значения Zc реальных газов и жидкостей [4]. Так, из уравнения Ван–дер-Вальса Zc=2,67, а для реальных газов Zс находится в пределах от 3,0 до 3,95, причем оно всегда больше 2,67. Невыполнимость уравнения (8) при подстановке в него hс объясняется тем, что в этом и подобных уравнениях согласно (1) используется плотность упаковки атомов в предшествующей более плотной фазе в точке ФТП. Полагаем, что в критической точке устанавливается состояние структуры вещества с регулярной плотностью упаковки сфер трехмерных колебаний атомов с предисторией ее при твердом полиморфном или кристаллическом состоянии, равной укладке атомов в гексагональной или в гранецентрированной (наиболее вероятных) решетках, где η1=0,74048 и Z=12, в тетрагональной (η1=0,6981; Z=10) или в объемно-центрированной (маловероятной) кристаллической решетке (η1=0,6802; Z=8). Вблизи критической точки развитие сильных флуктуаций плотности происходит по причине смены состояния структуры с регулярной укладкой сфер трехмерных колебаний атомов на случайную упаковку атомов. В прямолинейной зависимости координационного числа сфер трехмерных колебаний атомов от плотности их упаковки η1, коэффициенты при η1 становятся одинаковыми в окрестности критической точки. Следовательно, в критической точке ηс=(0,74048…0,6981)×ηсф, где ηсф – плотность упаковки атомов в сферах трехмерных их колебаний.
Второй подход к расчету координационного числа в сыпучих материалах и в твердой дисперсной фазе композитов основан на соответствии Zс=3…4 – критической плотности упаковки частиц на пороге предельного измельчения ηс≤0,2549. Учитывая непрерывность изменения фазотопологического состояния дисперсного слоя и соответствующее ему изменение плотности упаковки в нем частиц при его измельчении, прямолинейная интерполяция этого соответствия на произвольную величину плотности случайной упаковки невзаимодействующих и взаимодействующих частиц приводит к выражениям вида:
В работах российских и зарубежных исследователей структуры зернистого слоя, монодисперсных твердых шариков в слое отмечается один замечательный результат. Структура случайной упаковки твердых сферических частиц в зернистом слое хаpaктеризуется перманентностью локальных фрагментов с различной регулярной укладкой в них небольшого числа партикулярных частиц. Типы способов их укладки хорошо известны в кристаллохимии. При равной вероятности этих способов укладки в зернистом слое и соответствующих им координационных чисел, среднее координационное число в нем будет равно: Z= (12+10+8+8+6)/5 =8,8. Для случайной паковки идентичных частиц прямолинейная зависимость координационного числа в зернистом слое до наибольшей плотности их упаковки η1 =0,640289 при Z=8,8 будет иметь вид:
Среднее значение коэффициентов при η1 в уравнениях (9) и (10) дает аналогичный результат при η1 в уравнении (11). Из уравнения (11) при η1=0,574 и η1=0,59 Z=7,89 и Z=8,11. Экспериментальный результат при этом для частиц гранулированной сажи и стальных шариков соответственно равен: Z=7,87 и Z=8,06 [4].
Из уравнения (10) для случайной упаковки взаимодействующих частиц при η1=0,64029 получим Z=10. Преобразуем уравнение (3) для случайной упаковки частиц с учетом сил трения зацепления и заклинивания между ними в зернистом слое и сил адгезионного взаимодействия и вязкости в наполненных композитах до наибольшего значения Z=10 при η1=0,640289 следующим образом:
Отсюда, при η1=0,640289 с=3,602, а выражение для Z имеет вид:
Последний члeн в этом уравнении представляет собой зависимость коэффициента внутреннего трения зернистого слоя и композитов от η1: fвт=1,2η1, где с=1,2. Так, при η1=0,60…0,65…0,84 fвт=0,72…0,78… 1,0, что хорошо согласуется данными для кварцевого песка различной дисперсности. Для слабовзаимодействующих частиц со случайной их упаковкой в зернистом слое при η1=0,64029 и Z=8,8, при η1=0,6038 и Z=8 выражения, полученные подобно (12) будут имет вид:
Таким образом, для определения коэффициента внутреннего трения сыпучих материалов по формуле fвт=сη1 необходимо найти свободный члeн к уравнению (9), т.е. коэффициент «с» при Z=8,8 и η1≥0,6038 – для учета сил трения между частицами, а при η1≤0,6038 и Z=8 – для невзаи модействующих частиц округлой формы, либо коэффициент при η1 в уравнении (12) для данной плотности их упаковки в зернистом слое, а в композиционных материалах при Z=10.
Для всех значений Z≤8…10…12 и η≤0,68017…0,69813…0,74048 выражения для упрощенного расчета координационного числа взаимодействующих элементов структуры ме таллов в твердой и в жидкой фазе неупорядоченных систем получим путем преобразования уравнения (9) следующим образом:
Для исходных данных топологических параметров твердой фазы получим соответственно:
В уравнении (15) при Z=12 и η1=0,74048 выделим одну из величин плотности упаковки атомов в твердых металлах следующим образом:
Полученная при этом величина η1=0,726235 совпадает с плотностью упаковки атомов в гранецентрированной γ - полиморфной твердой модификации железа [5]. Вычисление по рекуррентному уравнению (1) при η1=0,726235 дает величину η=0,4722, совпадающей с ошибочной рекомендацией ее η=0,47±0,02 [6] для плотности упаковки атомов большинства жидких металлов. Из уравнения (15) для металлов при η1=0,73764… 0,72624…0,67468…0,66549…0,6505 получим: Z=11,95…11,76…10,93… 10,78…10,54. Первые две из этих величин относятся к твердой полиморфной фазе в точке ФТП. Следовательно уравнение (15) хорошо описывает многие металлы в полиморфных твердых и жидких модификациях, в тройной точке и в точке плавления с наличием жидкого полиморфизма к более плотным ГЦК и ГПУ структурам и кластерообразованию. Незначительное отличие уравнений (9) и (13) указывает на возможный легкий переход объемно-центрированной компактности сфер трехмерных колебаний атомов к случайной их упаковке, на неустойчивость высокотемпературных полиморфных модификаций с объемно-центрированной структурой в жидких металлах. При дальнейшем нагревании они переходят в случайную упаковку атомов, либо в плотнейшие гексагональную или гранецентрированную жидкую модификацию сфер трехмерных колебаний атомов в решетке с увеличением радиуса взаимодействия между ними. При критическом состоянии вещества объемно-центрированная компактность сфер трехмерных колебаний атомов маловероятна, либо совершенно невозможна.Учитывая, что в уравнении (1) выражение вид ln(120,754η15) дает число невзаимодействующих частиц, атомов или сфер их трехмерных колебаний с высокоплотной случайной упаковкой или с регулярной укладкой в фрагментах или в плотной фазе флуктуаций плотности, выражение для критического коэффициента в критической точке и вблизи нее следует записать в виде:
где с – силовая константа взаимодействия атомов, Z – наиболее вероятное число сфер трехмерных колебаний атомов в критической точке, Z=12…10.
Из уравнения (16) для ряда η1 с учетом полиморфизма: 0,74048; 0,73764; 0,72624; 0,710548; 0,70548; 0,6981; 0,68527; 0,6802 при с=1 и Z=12…10 получим ряд значений для Zс: 3,68…3,04; 3,67…3,06; 3,76…3,13; 3,89…3,24; 3,94…3,28; 4,0…3,34; 4,13…3,44; 4,18…3,49. Для дисперсного слоя частиц при Z=7,54 (9), Z=7,94 (4), Z=8,8 (11) согласно уравнению (16) при h1=0,6403 и с=1 получим: Zс=2,94; 3; 3,43; а при Z=10 (12) Zс=3,9. Как следует из результатов расчета, наиболее вероятное координационное число сфер трехмерных колебаний атомов в критической точке Z=10 с послойной гексагональной укладкой их в центре объема системы. В поле сил гравитации оно изменяется от низа к верху объема системы от Z=12 до Z=8. При этом возможно изменение Zс для слабовзаимодействующих элементов структуры: при Z=12 Zс=4,0, при Z=10 Zc=3,34, а при Z=8 Zc=2,67. Так, если среднее координационное число в неупорядоченной системе Z≤8, то для взаимодействующих элементов согласно (12) Z=10, в том числе и для большинства жидких систем и металлов Z=(12+10+8)/3=10 . Преобразуем уравнение (3) для учета взаимодействия (внутреннего трения) элементов структуры в жидкофазных системах путем приведения его к граничным параметрам кристаллических структур и тем самым найдем постоянную интегрирования в уравнении (2). Для граничных условий η1=0,74048 и =12 получим:
Отсюда, уравнение для возможно полного интервала значений Z с данным типом укладки элементов структуры имеем вид:
Последний члeн в этом уравнении с предистрией регулярной укладки атомов. Для приведения его к произвольной (случайной) упаковке атомов в жидкой фазе преобразуем его аналогичным (12) образом:
При η1≥0,4098 и η1≥0,38337 из этого уравнения получим соответственно Z≥2,18 и Z≥1,1, что указывает на число взаимодействующих атомов в газовой фазе. Аналогично получают уравнение для Z при граничных условиях для тетрагональной укладки при Z=10 и η1≥0,6981, для объемно- центрированной укладки при Z=8 и h ≥0,6802:
В полученных выше уравнениях (8, 8а, 8b) согласно выражениям (12) и (18) следует учитывать второй члeн, определяющий коэффициент внутреннего трения. Тогда полное выражение для критического коэффициента будет иметь вид:
где с=0,7085; 0,957; 1,2 – коэффициенты, хаpaктерные для данного типа структуры неупорядоченных систем (полиморфизма, кластеризации и случайной упаковки взаимодействующих элементов); kc=1,016423 – обобщенный коэффициент этого взаимодействия; kc=1,04609 – коэффициент для сильного взаимодействия, а kc=1,03826 – коэффициент для слабовзаимодействующих элементов неупорядоченных систем.
В уравнении (21) показатель n является неизвестной величиной, а величина knc зависит от индивидуальных свойств вещества, которая подлежит определению. Для известных значений Zc показатель n определяется подбором его значения для точного определения коэффициента внутреннего трения в виде:
fВ=cknc·з1 (22)
Для большинства сыпучих материалов n=0. Так, при kc=1,016423 и с=0,957 из выражения (21) для неона при n=3 Zc=3,34, для аргона при n=8-8,5 Zc=3,47-3,50; для криптона при n=19-20 Zc=3,48-3,54; для ксенона при n=3 Zc=3,074; при kc=1,04609 и n=1 для неона Zc=3,33 (3,33), при n=3-3,5 для аргона Zc=3,49-3,57 (3,49-3,54), при n=7 для криптона Zc=3,50 (3,50), при n=1 для ксенона Zc=3,06 (3,07). Из выражения (21) при kc=1,01642, с=1,2 и n=0 для неона Zc=3,336 (3,33) и ксенона Zc=3,076 (3,07); для аргона при n=2 и kc=1,04609 Zc=3,50 (3,49), а при kc=1,01642 и n=6 Zc=3,53 (3,54), для криптона при n=6 Zc=3,53 (3,50), а при kc=1,01642 и n=16 Zc=3,50 (3,50). В скобках приведены экспериментальные данные.
Поскольку первые члeны в уравнениях (17…20) исходят из случайной упаковки невзаимодействующих твердых сферических частиц, то поправка к ним на взаимодействие атомов в жидкой фазе определяется отношением плотности случайной упаковки твердых сфер, полученной из уравнения (1) для жидкой и псевдофазы из плотности их укладки в данной кристаллической решетке или полиморфной модификации, к фактической плотности упаковки атомов в жидкой фазе вещества - η1/ηж, а поправка ко вторым члeнам этих уравнений зависит от η1 и ее отклонения от таковой при случайной упаковке. При плавлении металлов жидкий полиморфизм и топологический беспорядок конкурирует в упаковке атомов в жидкой фазе, что приводит к повышению плотности их упаковки при наличии кластерных образований, либо к снижению ее при случайной их упаковке.
Следовательно, в точке плавления вещества при разрыхлении структуры в жидкой фазе в результате увеличения радиуса межмолекулярного взаимодействия получим:
где с – коэффициенты при η1 в уравнениях (18…20) для исходной данной кристаллической структуры; n – показатель, учитывающий влияние жидкого полиморфизма, кластеризации металлов или случайной упаковки атомов: n=0 – с преимуществом жидкого полиморфизма, n=1 – с преимуществом произвольной упаковки атомов в жидкой фазе при с=1,2, с=0,7085 и кластеризации атомов при с=0,957; значения η1 для данного типа кристаллической структуры или жидкой полиморфной модификации вычисляются из уравнения (1).
Приведем примеры расчета координационного числа в структуре жидких инертных газов и щелочных металлов при температуре плавления с учетом перегрева или переохлаждения.
В скобках приведены экспериментальные данные [1]. Данные для hж взяты из работы [1], а в скобках – справочные данные. Таким образом, жидкофазный полиморфизм металлов кластеризацию или случайную упаковку атомов в жидкой фазе можно обнаружить по равенству координационного числа, получаемого из радиальной функции распределения плотности и соответствующего вида одной из приведенных выше расчетных формул. Полученные уравнения для координационного числа в структуре неупорядоченных систем, наделенных дискретностью, позволяют с достаточной точностью вести расчет его величины для жидких металлов, коэффициента внутреннего трения этих систем и проектирование состава композиционных материалов с заданными свойствами.
Литература
- Скрышевский А.Ф. Структурный анализ жидкостей и аморфных тел. - М.: Высшая школа, 1980. - 328 с.
- Хархардин А.Н. Структурная топология неупорядоченных систем. // Вестник БелГТАСМ. Научно - теорет. ж - л. 2002. №2. - С.14 - 27.
- Беляев Н.М. Термодинамика. - Киев:Выща школа, 1987. - С. 36 - 37.
- Аэров М.Э., Тодес О.М. Гидравлические и тепловые основы работы аппаратов со стационарным и кипящим зернистым слоем. - Л.: Химия, 1968. - С. 8 - 52.
- Ахметов Н.С. Неорганическая химия.- М.: Высшая школа, 1975 - С. 619.
- Харьков Е.И., Лысов В.И., Федоров В.Е. Физика жидких металлов. - Киев. Выща школа,1979. - 247с.
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
22 04 2024 15:29:59
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
21 04 2024 19:58:26
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
19 04 2024 17:54:54
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
18 04 2024 22:27:56
 Статья в формате PDF
254 KB...
Статья в формате PDF
254 KB...
17 04 2024 22:48:48
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
14 04 2024 12:41:18
 На конкретных примерах показана возможность применения принципа «наследственное ядро – динамическое окружение» к составлению математических (статистических) моделей многомерных воспроизводственно-циклических экономических явлений и процессов. В статье ставятся две цели: во-первых, на примере распределения предприятий Германии [4] показать популяционные закономерности, то есть доказать схожесть распределения предприятий по численности рабочих с популяциями живых существ; во-вторых, показать модели социальной динамики по данным групп семейных бюджетов Швеции и дать математическое осмысление закона убывающей доходности Гутенберга.
...
На конкретных примерах показана возможность применения принципа «наследственное ядро – динамическое окружение» к составлению математических (статистических) моделей многомерных воспроизводственно-циклических экономических явлений и процессов. В статье ставятся две цели: во-первых, на примере распределения предприятий Германии [4] показать популяционные закономерности, то есть доказать схожесть распределения предприятий по численности рабочих с популяциями живых существ; во-вторых, показать модели социальной динамики по данным групп семейных бюджетов Швеции и дать математическое осмысление закона убывающей доходности Гутенберга.
...
12 04 2024 1:56:56
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
09 04 2024 1:29:55
07 04 2024 15:39:10
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
06 04 2024 2:42:52
04 04 2024 0:25:16
 Статья в формате PDF
630 KB...
Статья в формате PDF
630 KB...
03 04 2024 23:47:19
 Статья в формате PDF
130 KB...
Статья в формате PDF
130 KB...
02 04 2024 18:58:42
 Статья в формате PDF
294 KB...
Статья в формате PDF
294 KB...
01 04 2024 7:54:34
 Статья в формате PDF
102 KB...
Статья в формате PDF
102 KB...
31 03 2024 21:33:44
 Статья в формате PDF
306 KB...
Статья в формате PDF
306 KB...
29 03 2024 8:54:12
 Статья в формате PDF
139 KB...
Статья в формате PDF
139 KB...
27 03 2024 5:50:11
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
26 03 2024 0:50:15
 Предложен новый подход к изучению земного магнетизма. В центре Земли монополь µ, шаровая молния возникает в пучностях стоячих волн монополя. Гравитация – квадрупольное излучение µ.
...
Предложен новый подход к изучению земного магнетизма. В центре Земли монополь µ, шаровая молния возникает в пучностях стоячих волн монополя. Гравитация – квадрупольное излучение µ.
...
25 03 2024 3:52:29
 Статья в формате PDF
332 KB...
Статья в формате PDF
332 KB...
23 03 2024 3:54:23
 Статья в формате PDF
489 KB...
Статья в формате PDF
489 KB...
22 03 2024 8:58:58
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
21 03 2024 3:51:44
 Статья в формате PDF
131 KB...
Статья в формате PDF
131 KB...
19 03 2024 16:11:40
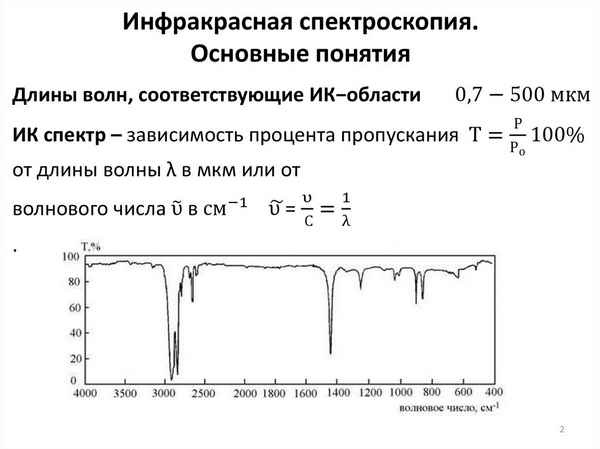 Представлены результаты исследований инфpaкрасных спектров поглощения в образцах высушенной капли мочи. Применение метода ИК – спектроскопии для исследования образцов мочи в виде высушенной капли позволяет повысить диагностическую значимость молекулярного анализа. Полученные результаты могут быть использованы при разработке новых методов ранней диагностики различных заболеваний.
...
Представлены результаты исследований инфpaкрасных спектров поглощения в образцах высушенной капли мочи. Применение метода ИК – спектроскопии для исследования образцов мочи в виде высушенной капли позволяет повысить диагностическую значимость молекулярного анализа. Полученные результаты могут быть использованы при разработке новых методов ранней диагностики различных заболеваний.
...
18 03 2024 11:36:31
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
17 03 2024 17:27:47
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::