РАЗМЕРНОСТИ ФИЗИЧЕСКИХ ВЕЛИЧИН В СИСТЕМЕ ИЗМЕРЕНИЙ СБК-2LT
В работе [6] представлено краткое описание системы единиц физических величин СБК-2LT, имеющей две основные размерности и, соответственно, две основные единицы измерения физических величин. Однако в [6] из-за ограниченности объема публикации описаны лишь принципы, положенные в основу построения этой системы измерений, и приведены размерности лишь для некоторых физических величин (таких как масса, электрический заряд, количество магнетизма, X-заряд [4], сила электрического тока, электрическое сопротивление и электрическая проводимость).
Целью данной работы является составление таблицы размерностей физических величин для системы измерений СБК-2LT, охватывающей значительно большее количество физических величин. Эта статья является продолжением работы [6], дополняющим последнюю.
В основе системы единиц физических величин СБК-2LT лежит международная систем единиц физических величин СИ. При этом система СБК-2LT получена не в результате искусственного подбора базовых размерностей и основных единиц измерения, а в результате естественной трaнcформации системы СИ в сторону ее упрощения на основе закона бинарной комплементарности фундаментальных взаимодействий [4], дипольно-тоннельной гидродинамической теории гравитационного взаимодействия и электромагнитных явлений [2, 3 и др.] и постулатов о тождественности фундаментальных зарядов [5].
Аббревиатура «СБК» в названии системы СБК-2LT расшифровывается как «Система единиц физических величин, основанная на законе Бинарной Комплементарности фундаментальных взаимодействий», а «2» - это количество основных (базовых) размерностей системы СБК-2LT, которыми являются две размерности: L - размерность длины и T - размерность времени. Соответственно основными единицами СБК-2LT являются «метр» (м) и «секунда» (с) для всех физических величин, как механики, так и электричества и магнетизма.
При этом (на основании [2-6]) единицы измерения «килограмм» (кг) и «ампер» (А), использующиеся в системе СИ, выражаются следующим образом:
(1)
(2)
где G* - безразмерная величина, численно равная значению гравитационной постоянной в системе СИ; G* = 6,67259(85)⋅10-11; c* - безразмерная величина, численно равная значению скорости света в вакууме в системе СИ; c* ≈ 2,99792458⋅10-8; - безразмерная величина, численно равная значению магнитной постоянной в системе СИ; π ≈ 3,14159.
Выражения (1) и (2) получены следующим образом.
В [5] представлены два постулата о тождественности фундаментальных зарядов, которые являются дополнениями к закону бинарной комплементарности фундаментальных взаимодействий, сформулированному в [4] авторами данной статьи. Область действия постулатов охватывает вакуум (а также, возможно, другие среды) и распространяется на четыре вида фундаментальных взаимодействий, - гравитационное, магнитное, электрическое и фундаментальное X-взаимодействие (о нем см. [4]). При формулировке постулатов сильное и слабое взаимодействия не принимались в рассмотрение, поскольку до сих пор не доказана «самостоятельность» этих взаимодействий, т.е. их несводимость к перечисленным выше взаимодействиям или к комбинациям последних. Существуют гипотезы и теории, в соответствии с которыми сильное и слабое взаимодействия являются специфическими проявлениями перечисленных выше или более общих (например, теория «Великого объединения») взаимодействий при малых расстояниях между объектами взаимодействий [2, 3, 8 и др.].
Под фундаментальными зарядами здесь и в [4-6] подразумеваются: количество электричества (электрический или, иначе, кулоновский заряд) - при электрическом взаимодействии; количество магнетизма - при магнитном взаимодействии; масса (гравитационный заряд) - при гравитационном взаимодействии; X-заряд - при фундаментальном X-взаимодействии, комплементарном гравитационному взаимодействию (краткая хаpaктеристика фундаментального X-взаимодействия представлена в [4]).
В соответствии с первым из упомянутых выше постулатов [5] все фундаментальные заряды тождественны друг другу по размерности. Согласно второму постулату [5] фундаментальные заряды разного типа могут быть тождественны друг другу по абсолютному значению.
Фундаментальные заряды qI и qII разного типа (например, qI - электрический заряд, а qII - масса) считаются равными друг другу, т.е.
qI = qII, (3)
если в вакууме выполняется равенство
FI = FII, (4)
где FI - сила взаимодействия двух одинаковых по величине зарядов qI, удаленных друг от друга на расстояние r; FII - сила взаимодействия двух одинаковых по величине зарядов qII, удаленных друг от друга на то же расстояние r.
В соответствии, например, с [11, 14]:
(5)
(6)
где G - гравитационная постоянная;
G = 6,6729(85)⋅10-11 м3/(кг⋅с2) (в системе СИ);
ε0 - электрическая постоянная;
ε0 ≈ 8,854187817)⋅10-12 Ф/м (в системе СИ);
(7)
где μ0 - магнитная постоянная;
μ0 ≈ 12,566370614⋅10-7 Н/А2 (в системе СИ); c - скорость света в вакууме;
c ≈ 2,99792458⋅108 м/с (в системе СИ);
m - масса; qE - электрический заряд; qM - количество магнетизма («магнитный заряд», если использовать терминологию формальной теории магнетизма [9]).
Из (4) с учетом (3), (5) и (6) следует, что
(8)
(9)
(10)
Выражения (8)-(10) можно представить следующим образом:
(11)
(12)
(13)
где [G], [ε0], [μ0] - размерности в системе СИ физических величин G, ε0 и μ0 соответственно; - безразмерная величина, численно равная значению электрической постоянной в системе СИ;
;
(14)
(15)
(16)
где M - размерность массы (соответствующая ей единица измерения в системе СИ - килограмм, кг); I - размерность силы электрического тока (соответствующая ей единица измерения в системе СИ - ампер, А).
Из совместного решения уравнений (11)-(13) с учетом (14)-(16) получаются выражения
(17)
(18)
а также выражение (2). Выражение (1) является результатом совместного решения уравнений (2) и (17) с учетом (7).
Система СБК-2LT получается из системы измерений СИ путем замены размерности M на размерность L2T-1, а также замены размерности I на размерность L2T-1, т.е.
(19)
(20)
При этом значения фундаментальных физических констант (а также и прочих численных значений) в системе СБК-2LT получаются из соответствующих численных значений, взятых из системы СИ, путем замены в последних единиц измерения «килограмм» и «ампер» в соответствии с выражениями (1) и (2).
В системе СБК-2LT размерность всех фундаментальных зарядов (количества электричества - при электрическом взаимодействии; количества магнетизма - при магнитном взаимодействии; массы - при гравитационном взаимодействии; X-заряда - при фундаментальном X -взаимодействии, комплементарном гравитационному взаимодействию [4, 5]) равна L2T-1, а их единицами измерения является метр квадратный, деленный на секунду, т.е м2/c. Указанная размерность фундаментальных зарядов отличается от размерностей этих зарядов, приведенных, например, в [1, 10, 13, 15].
В соответствии с (19) и (20) авторами данной работы были получены размерности для физических величин, перечисленных в разделах «Механика» и «Электричество и магнетизм» табл. 3 Приложения 1 «Международная система единиц (СИ) и ее применение», приведенной в [11] на с. 636-637. Ниже эти размерности представлены в табл. 1 и 2.
На основе данных, приведенных в табл. 1 и 2, построена сводная таблица размерностей основных физических величин в системе СБК-2LT, представленная на рис. 1.
Минимальные и максимальные значения размерностей L и T физических величин в системе СБК-2LT приведены в табл. 3, где i - степень размерности L; j - степень размерности T.
В табл. 3 обращает на себя внимание выделенная цветом последовательность ячеек, образующих ось «время (В) - длина (Д) - масса (М) - количество движения (КД) - энергия (Э)» (ось В-Э), которая может быть представлена в виде графика в координатах i-j (рис. 2).
При этом ось В-Э описывается выражением
j = 1 - i. (21)
1. Размерности единиц физических величин в системе СБК-2LT
Механика
|
Размерность |
Физические величины |
|
L-1 T-1 |
Прострaнcтвенная плотность вещества |
|
L1T1 |
Удельный объем |
|
L1T-2 |
Динамическая вязкость |
|
L1T-3 |
Давление Механическое напряжение (нормальное напряжение, касательное напряжение) Модуль продольной упругости, модуль сдвига, модуль объемного сжатия |
|
L2T-1 |
Масса Х-заряд (заряд, комплементарный гравитационному заряду, т.е. массе) Кинематическая вязкость |
|
L2T-3 |
Поверхностное натяжение |
|
L3T-2 |
Количество движения Импульс силы |
|
L3T-3 |
Сила, сила тяжести (вес) |
|
L4T-1 |
Момент инерции (динамический момент инерции) |
|
L4T-2 |
Момент количества движения |
|
L4T-3 |
Работа Энергия Момент силы, момент пары сил |
|
L4T-4 |
Мощность |
2. Размерности единиц физических величин в системе СБК-2LT.
Электричество и магнетизм
|
Размерность |
Физические величины |
|
L-1 T1 |
Абсолютная магнитная проницаемость Абсолютная диэлектрическая проницаемость |
|
L-1 T0 |
Удельная электрическая проводимость |
|
L-1 T-1 |
Прострaнcтвенная плотность электрического заряда |
|
L0T1 |
Индуктивность, взаимная индуктивность Электрическая емкость Магнитная проводимость |
|
L0T0 |
Электрическое сопротивление (активное, реактивное, полное) Электрическая проводимость (активная, реактивная, полная) |
|
L0T-1 |
Магнитная индукция Магнитное сопротивление Поверхностная плотность электрического заряда Электрическое смещение |
|
L0T-2 |
Плотность электрического тока |
|
L1T0 |
Удельное электрическое сопротивление |
|
L1 T-2 |
Напряженность электрического поля Напряженность магнитного поля Намагниченность (интенсивность намагничивания) Линейная плотность электрического тока |
|
L2T-1 |
Количество электричества (электрический заряд) Магнитный поток (количество магнетизма) |
|
L2T-2 |
Электрический ток Электрическое напряжение Электродвижущая сила Магнитодвижущая сила Электрический потенциал Разность магнитных потенциалов Поток электрического смещения |
|
L3T-1 |
Электрический момент диполя Магнитный момент (кулоновский) |
|
L4T-2 |
Магнитный момент (амперовский) |
Физические величины, располагающиеся на оси В-Э, объединяет то, что, по крайней мере, для четырех из них (для массы, электрического заряда, количества движения и энергии) существуют известные законы сохранения.
В связи с этим можно предложить более общий закон сохранения, охватывающий все физические величины, лежащие на оси, описывающейся выражением (21) и имеющие размерности LiT1-i в системе измерений СБК-2LT, где i ∈ ]-∞; +∞[.
Применение системы СБК-2LT позволяет упростить некоторые физические уравнения. В частности, в системе СБК-2LT уравнение связи между двумя комплементарными фундаментальными зарядами qA и qB (т.е. зарядами, относящимися к двум разным, но взаимно-комплементарным взаимодействиям; например, qA - электрический заряд, а qB - количество магнетизма; или qA - масса, а qB - X-заряд)
(22)
приведенное в [4], может быть получено в более простом виде:
(23)
или
(24)
где NA - поверхностная плотность заряда qB; ; S - площадь; EA - скорость изменения заряда qA во времени; ; t - время; m - масса; gA - массовая плотность заряда qA; ; k - коэффициент пропорциональности.
Рис. 1. Система единиц физических величин СБК-2LT
(основные единицы прострaнcтва и времени, механики, электричества и магнетизма)
3. Минимальные и максимальные значения размерностей L и T в системе СБК-2LT
|
Минимальное значение |
Максимальное значение |
|
|
i |
-1 |
4 |
|
j |
-4 |
1 |
Рис. 2. Ось В-Э в координатах i-j
Соответствия между комплементарными фундаментальными зарядами qA и qB (т.е. все возможные сочетания комплементарных пар qA - qB) показаны в табл. 4, где qX - X-заряд, комплементарный гравитационному заряду (т.е. массе). В соответствии с законом бинарной комплементарности фундаментальных взаимодействий [4] и исходя из современных знаний о фундаментальных взаимодействий, - на сегодняшний день выявлены две комплементарные пары: электромагнитная (электрическое и магнитное взаимодействия) и X-гравитационная (гравитационное и комплементарное ему X-взаимодействие). Факт существования фундаментального X-взаимодействия подтверждается результатами экспериментальных исследований неэлектромагнитного силового взаимодействия вращающихся тел в вакууме, проведенных доктором технических наук, профессором В.Н. Самохваловым [12].
4. Соответствия между комплементарными фундаментальными зарядами
|
Комплементарные пары |
Соответствия между |
|
|
Фундаментальный заряд qA |
Фундаментальный заряд qB, |
|
|
Электромагнитная |
qE |
qM |
|
qM |
qE |
|
|
Гравитационная |
m |
qX |
|
qX |
m |
|
На основе системы единиц физических величин СБК-2LT и первого постулата о тождественности фундаментальных зарядов [5] были получены системы измерений СБК-1T и СБК-1L, каждая из которых имеет только одну размерность и, соответственно, одну единицу измерения физических величин. Краткое описание этих систем приведено в [7].
Система измерений СБК-2LT отличается от других известных аналогичных систем, имеющих две основные размерности L и T и приведенных, например, в [1, 10, 13, 15].
Несмотря на то, что система единиц физических величин СБК-2LT является более простой, чем система измерений СИ, из которой она была получена, - авторы этой работы не рассматривают систему СБК-2LT как альтернативный вариант системе СИ. По мнению авторов, использование системы СИ на пpaктике в большинстве случаев является более удобным и рациональным, чем использование системы СБК-2LT. Однако последняя система представляет интерес с чисто научной (познавательной) точки зрения, лишний раз указывает на сложность, многогранность и, в то же время, четкую внутреннюю организацию и симметрию материи.
В заключение следует также отметить, что помимо систем измерений СБК-2LT, СБК-1T и СБК-1L на основе совместного решения уравнений (2), (17) и (18) авторами данной статьи были разработаны следующие системы единиц физических величин:
- имеющие две основные размерности: СБК-2LM (основные размерности L и M) и СБК-2MT (основные размерности M и T)
- системы, имеющие три основные размерности: СБК-3LTI (основные размерности L, T и I) и СБК-3LMT (основные размерности L, M и T).
Из-за ограниченного объема статьи в нее не вошли описания этих систем, которые будут представлены в последующих публикациях авторов данной работы.
Список литературы
- Бартини Р.Л. Некоторые соотношения между физическими константами // Доклады Академии наук СССР. - 1965. - Т. 163, № 4. - С. 861-864.
- Бражников А.В., Юмшин Д.В., Хомич Л.В. Основные положения гидродинамической теории гравитационного взаимодействия и электромагнитных явлений // Сборник материалов межрегиональной научной конференции «Молодежь и наука - третье тысячелетие». - Красноярск: Изд-во КРО НС «Интеграция», 2005. - С. 260-265.
- Бражников А.В., Гилев А.В., Белозеров И.Р. Факты, свидетельствующие в пользу дипольно-тоннельной гидродинамической теории гравитационного взаимодействия и электромагнитных явлений // Фундаментальные исследования. - 2009. - № 5. - С. 9-10.
- Бражников А.В., Белозеров И.Р. Закон бинарной комплементарности фундаментальных взаимодействий // Современные проблемы науки и образования. - 2010. - № 6 (приложение «Физико-математические науки»). - С. 4.
- Бражников А.В., Белозеров И.Р. Постулаты о тождественности фундаментальных зарядов // Современные проблемы науки и образования. - 2010. - № 6 (приложение «Физико-математические науки»). - С. 5.
- Бражников А.В., Белозеров И.Р. Система единиц физических величин СБК-2LT // Современные проблемы науки и образования. - № 6 (приложение «Физико-математические науки»), 2010. - С. 6.
- Бражников А.В., Белозеров И.Р. Системы единиц физических величин СБК-1T и СБК-1L // Современные проблемы науки и образования. - 2010. - № 6 (приложение «Физико-математические науки»). - С. 7.
- Бухбиндер И.Л. Фундаментальные взаимодействия // Опубликовано в «Соровском образовательном журнале». - 1997. - № 5.
- Калашников С.Г. Электричество. - М.: Наука, 1964. - 668 с.
- Новицкий В. «Камень преткновения» в физике? // Техника - молодежи. - 1990. - № 5. - С. 18-21.
- Политехнический словарь / под ред. А.Ю. Ишлинского. - М.: Советская энциклопедия, 1989. - 656 с.
- Самохвалов В.Н. Давление квадрупольного излучения вращающихся масс на твердые тела. - http://www.sciteclibrary.ru/rus/catalog/pages/10206.html .
- Чуев А.С. Физическая картина мира в размерности «длина-время». Серия «Информатизация России на пороге XXI века». - М.: СИНТЕГ, 1999. - 96 с.
- Яворский Б.М., Детлаф А.А. Справочник по физике. - М.: Наука, 1980. - 512 с.
- Roberto Oros di Bartini. Relations Between Physical Constants // Progress in Physics. - 2005. - Vol. 5. - P. 34-40.
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
24 04 2024 18:12:59
23 04 2024 11:11:26
 Статья в формате PDF
304 KB...
Статья в формате PDF
304 KB...
22 04 2024 5:53:49
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
20 04 2024 8:44:39
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
19 04 2024 11:14:18
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
18 04 2024 2:55:59
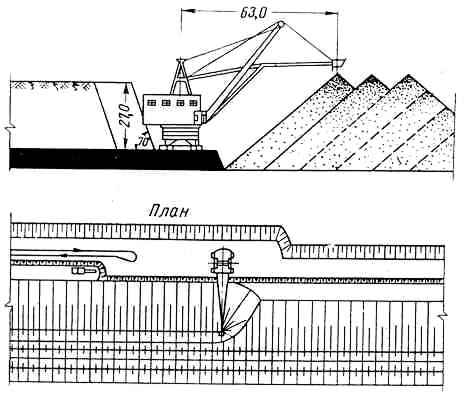 Изложены результаты технолого-экологической оценки выемки междупластья по бестрaнcпортной технологии на Кангаласском угольном разрезе.
...
Изложены результаты технолого-экологической оценки выемки междупластья по бестрaнcпортной технологии на Кангаласском угольном разрезе.
...
17 04 2024 20:29:37
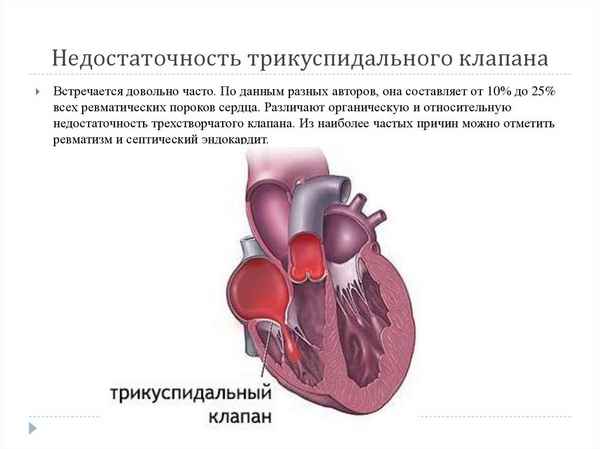
 В данной статье говориться о морфологических изменениях в стенках крупных артерии мышечного типа и слизистой оболочки желудка крыс в ходе эксперимента, вызванные двигательной активностю и ее ограничением. Основные изменения наблюдались в стенках слизистой оболочки желудка и ее артериях.
...
В данной статье говориться о морфологических изменениях в стенках крупных артерии мышечного типа и слизистой оболочки желудка крыс в ходе эксперимента, вызванные двигательной активностю и ее ограничением. Основные изменения наблюдались в стенках слизистой оболочки желудка и ее артериях.
...
16 04 2024 6:34:55
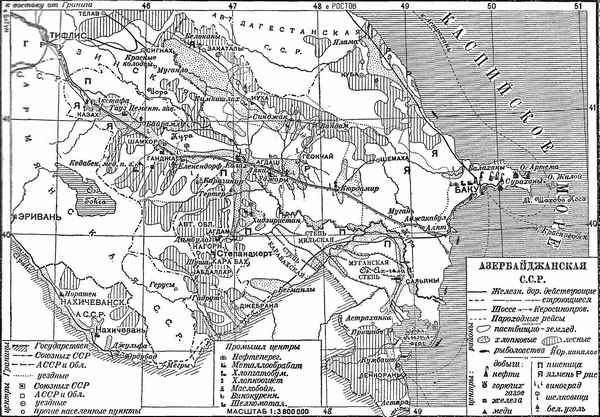 Проведен сравнительный анализ результатов популяционно-генетических исследований по выявлению легкодиагностируемых врожденных пороков развития и наследственных заболеваний среди населения Муганской и Ширванской зон Азербайджана. Установлена высокая частота распространения нарушений ЦНС, аномалий скелета и врожденных патологий зрения. С использованием молекулярного метода полимеразно-цепной реакции идентифицированы типы мутаций β-талассемии в обследованных зонах. Планируется проведение пренатальной диагностики талассемии.
...
Проведен сравнительный анализ результатов популяционно-генетических исследований по выявлению легкодиагностируемых врожденных пороков развития и наследственных заболеваний среди населения Муганской и Ширванской зон Азербайджана. Установлена высокая частота распространения нарушений ЦНС, аномалий скелета и врожденных патологий зрения. С использованием молекулярного метода полимеразно-цепной реакции идентифицированы типы мутаций β-талассемии в обследованных зонах. Планируется проведение пренатальной диагностики талассемии.
...
15 04 2024 8:17:30
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
14 04 2024 16:35:47
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
13 04 2024 3:33:42
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
12 04 2024 13:30:37
 Статья в формате PDF
139 KB...
Статья в формате PDF
139 KB...
11 04 2024 20:21:13
Статья в формате PDF 92 KB...
10 04 2024 13:27:21
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
09 04 2024 1:59:47
 Обучение любому иностранному языку начинается, как правило, с обучения фонетике. Каждый национальный язык имеет свою неповторимую индивидуальную фонетическую систему, которая говорящим на этом языке представляется самой удобной. Фонетическая система вьетнамского языка сильно отличается от фонетической системы русского. Для вьетнамских студентов работа по обучению произношению должна строиться с учётом особенностей вьетнамского языка. В статье были показаны всевозможные трудности в обучении фонетике русского языка вьетнамских студентов, начиная с обучения звуков русской речи до интонации. Вместе с тем были предложены способы устранения ошибок при обучении фонетике русского языка вьетнамских студентов.
...
Обучение любому иностранному языку начинается, как правило, с обучения фонетике. Каждый национальный язык имеет свою неповторимую индивидуальную фонетическую систему, которая говорящим на этом языке представляется самой удобной. Фонетическая система вьетнамского языка сильно отличается от фонетической системы русского. Для вьетнамских студентов работа по обучению произношению должна строиться с учётом особенностей вьетнамского языка. В статье были показаны всевозможные трудности в обучении фонетике русского языка вьетнамских студентов, начиная с обучения звуков русской речи до интонации. Вместе с тем были предложены способы устранения ошибок при обучении фонетике русского языка вьетнамских студентов.
...
08 04 2024 12:43:10
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
05 04 2024 17:13:27
 Статья в формате PDF
189 KB...
Статья в формате PDF
189 KB...
04 04 2024 9:13:57
 Статья в формате PDF
265 KB...
Статья в формате PDF
265 KB...
03 04 2024 2:41:42
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
02 04 2024 21:28:43
 Статья в формате PDF
476 KB...
Статья в формате PDF
476 KB...
01 04 2024 21:24:55
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
31 03 2024 3:36:34
 Статья в формате PDF
173 KB...
Статья в формате PDF
173 KB...
30 03 2024 16:50:56
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
29 03 2024 15:25:35
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
28 03 2024 18:28:11
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
27 03 2024 6:56:22
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
26 03 2024 4:21:47
 Статья в формате PDF
245 KB...
Статья в формате PDF
245 KB...
25 03 2024 6:37:18
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
24 03 2024 20:58:39
 Статья в формате PDF
271 KB...
Статья в формате PDF
271 KB...
23 03 2024 18:22:17
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
22 03 2024 19:17:31
 Статья в формате PDF
274 KB...
Статья в формате PDF
274 KB...
21 03 2024 21:22:32
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
20 03 2024 12:19:27
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
19 03 2024 13:33:52
Статья в формате PDF 302 KB...
18 03 2024 4:19:16
 Статья в формате PDF
139 KB...
Статья в формате PDF
139 KB...
17 03 2024 23:53:39
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::