ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ГРУЗА ПРИ НАЛИЧИИ НЕУДЕРЖИВАЮЩЕЙ СВЯЗИ С ИЗМЕНЯЕМОЙ ГЕОМЕТРИЕЙ
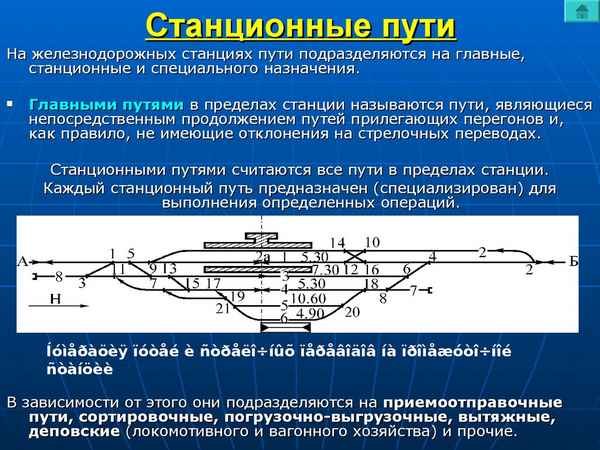
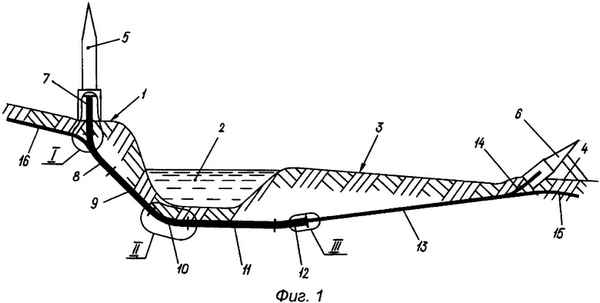
Рассмотрим движение груза M массой m, подвешенной на невесомой нерастяжимой нити бесконечной длины, намотанной на неподвижный цилиндр радиуса r. В положении устойчивого равновесия длина свободной части нити равна l0 (рис. 1), размерами груза пренебрегаем.
Рис. 1. Расчетная схема
В произвольный момент времени положение материальной точки определим радиус-вектором , в качестве обобщенной координаты примем ее угол отклонения от положения устойчивого равновесия j. Кроме силы тяжести на точку действует идеальная связь - нерастяжимая нить (рис. 1), действие которой, заменим ее реакцией - силой натяжения .
Дифференциального уравнения движения
(1)
здесь T - кинетическая энергия, - потенциальная энергия.
(2)
Здесь - скорость материальной точки,
где тогда
(3)
Подставляя выражения (2), (3) в уравнение Лагранжа (1) получим дифференциальное уравнение движения груза
(4)
Начальные условия для уравнения (4) имеют вид
(5)
Движение материальной точки будет описываться дифференциальным уравнением (4) с начальными условиями (5) до тех пор, пока связь, наложенная на данную точку, остается удерживающей, т. е. выполняется условие x2 + y2 + l2 или N ≥ 0. Кроме этого, должно выполняться дополнительное условие
l0 + rφ > 0 или (6)
которое обеспечивает отсутствие соударения груза с поверхностью неподвижного цилиндра.
С учетом (6) уравнение (4) можно записать в виде
(7)
где - приведенный радиус неподвижного цилиндра,
Для нахождения реакции нити запишем основное уравнение динамики несвободной материальной точки в проекциях на нормаль к траектории, которая совпадает с линией AM:
Тогда значение силы N будет равно
(8)
где - приведенная угловая скорость отклонения нити от вертикали, - сила натяжения, отнесенная к весу груза.
Для анализа дифференциального уравнения движения (7) запишем его первый интеграл, выражающий закон сохранения механической энергии
.
С учетом соотношений (2) и (3), получим
Данное выражение можно привести к виду
(9)
где
Выражение для силы натяжения нити (8) с учетом (9) запишется в виде
(10)
где
Анализ задачи показывает, что возможны два вида движения точки, описываемой дифференциальным уравнением (7): колебательное, вблизи положения устойчивого равновесия и движение по раскручивающейся спирали.
Положение устойчивого равновесия определяется из условия минимума потенциальной энергии точки
Согласно выражению (3) получим
Так как B(φ) > 0, а угол β изменяется внутри интервала , то положения устойчивого равновесия соответствует значениям φ равным
φ = 0,2πn; n ∈ N.
График изменения потенциальной энергии материальной точки представлен на рис. 2. При расчетах принято, что l0 = π r, т.е. αкр = π.
Рассмотрим теперь предельные состояния движения груза, при которых осуществляется переход от одного вида движения к другому. Преобразуем выражение (9) к виду:
(11)
где
.
Анализ выражения позволяет сделать вывод о том, что параметр σ хаpaктеризует два вида движения точки: колебательное и движение по раскручивающейся спирали.
Рис. 2. Области на фазовой плоскости:
I - колебательного движения;
II - движение по раскручивающейся спирали
При значениях 0 < σ ≥ 1 его можно представить в виде и выражение (11) запишется в виде
откуда следует, что и , т.е. движение носит колебательный хаpaктер, максимальное отклонение которого α определится из уравнения:
При значениях σ > 1 величина в любой момент времени и груз совершает движение по раскручивающейся спирали.
Таким образом, предельным, разделяющим два движения груза, является уравнение σ = 1 (рис. 2), которое можно записать в виде:
или
При значениях груз совершает движение по раскручивающейся спирали, а при значениях - колебательное движение. Следовательно, при колебательном движении груза, его максимальное отклонение от положения устойчивого равновесия не может превышать величину
Список литературы
- Бертяев В.Д. Теоретическая механика на базе Mathcad. Пpaктикум: учебное пособие. - СПб, БХВ - Петербург, 2005. - 752 с.
- Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. - ч. 1, 2. - М.: Наука, 1983.
Статья в формате PDF
122 KB...
09 03 2026 12:53:23
Статья в формате PDF
107 KB...
08 03 2026 14:27:20
Статья в формате PDF
134 KB...
07 03 2026 5:12:29
Приводятся результаты исследования восстановления пашен, заброшенных при развитии негативных криогенных процессов и явлений и деформации поверхности. Этот опыт восстановления может использоваться и на долинных сельскохозяйственных угодьях, где распространены близкозалегающие подземные льды, вызывающие деформацию поверхности при мелиоративных воздействиях.
...
06 03 2026 7:26:44
Статья в формате PDF
110 KB...
05 03 2026 23:17:35
Статья в формате PDF
116 KB...
04 03 2026 8:11:27
Статья в формате PDF
96 KB...
03 03 2026 5:20:56
Статья в формате PDF
179 KB...
02 03 2026 2:36:54
Статья в формате PDF
253 KB...
01 03 2026 19:27:51
Статья в формате PDF
148 KB...
28 02 2026 8:22:30
Статья в формате PDF
105 KB...
27 02 2026 1:18:16
Статья в формате PDF
123 KB...
26 02 2026 12:29:17
Статья в формате PDF
264 KB...
25 02 2026 8:28:41
Статья в формате PDF
106 KB...
24 02 2026 15:19:42
Статья в формате PDF
120 KB...
23 02 2026 17:22:12
Статья в формате PDF
113 KB...
22 02 2026 6:15:29
Статья в формате PDF
154 KB...
21 02 2026 5:26:19
Статья в формате PDF
331 KB...
20 02 2026 21:29:43
Статья в формате PDF
164 KB...
19 02 2026 13:29:58
Статья в формате PDF
90 KB...
16 02 2026 7:11:13
Статья в формате PDF
103 KB...
15 02 2026 8:20:43
Статья в формате PDF
93 KB...
14 02 2026 6:32:10
Статья в формате PDF
102 KB...
13 02 2026 15:37:43
Статья в формате PDF
105 KB...
12 02 2026 8:52:57
Статья в формате PDF
126 KB...
11 02 2026 4:57:28
Статья в формате PDF
114 KB...
10 02 2026 20:19:55
Выделены навыки социальной коммуникации, необходимые для успешного освоения химических дисциплин. Предложен один из путей снятия напряженности в процессе общения преподавателя и студента - виртуальный письменный диалог, реализованный в виде учебного пособия. Используемые в пособии методические приемы позволяют наиболее полно сформировать необходимый инструментарий познания: (логические операции + социальная коммуникация) → понимание → знание.
...
08 02 2026 15:30:53
Статья в формате PDF
288 KB...
07 02 2026 3:48:58
Статья в формате PDF 281 KB...
06 02 2026 12:55:42
Статья в формате PDF
120 KB...
05 02 2026 21:35:56
Статья в формате PDF
250 KB...
04 02 2026 13:50:12
Статья в формате PDF
119 KB...
03 02 2026 3:55:28
Статья в формате PDF
136 KB...
01 02 2026 12:43:37
Статья в формате PDF
384 KB...
31 01 2026 22:11:35
Статья в формате PDF
320 KB...
30 01 2026 6:31:26
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
