ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ

равнения существует, когда оно единственно, решается так называемыми теоремами существования и единственности. Эти теоремы очень важны, как для самой теории, так и для пpaктики. Они гарантируют законность применения качественных методов теории дифференциальных уравнений для решения задач естествознания и техники. Численному интегрированию дифференциального уравнения обязательно должно предшествовать обращение к теоремам существования и единственности. И это необходимо делать для того, чтобы избежать недоразумений или вообще неправильных выводов.
Теорема существования. Если в уравнении
(1) функция f определена и непрерывна в некоторой ограниченной области D плоскости (x, y), то для любой точки (x0, y0) € D существует решение y(x) начальной задачи, y(x0) = y0, (2)
определенное на некотором интервале, содержащем точку x0.
Теорема существования и единственности. Если в уравнении функция f определена и непрерывна в некоторой ограниченной области D плоскости (x,y), причем она удовлетворяет в области D условию Липшица по переменной y, т.е.
Теорема о продолжении. При выполнении условий теоремы существования или теоремы существования и единственности всякое решение уравнения с начальными данными (x0, y0) Î D может быть продолжено до точки, сколь угодно близкой к границе области D. При этом в первом случае продолжение, вообще говоря, будет не обязательно единственным, во втором же случае оно единственно.
Для иллюстрации «недоразумений» возникающих при использовании численных решений дифференциальных уравнений без учета теорем существования рассмотрим несколько примеров.
Пример 1. Требуется, используя численный метод интегрирования Эйлера с итерационной схемой
c шагом h =0,1, решить начальную задачу
y(-1) = 0,21 (3)
на отрезке [-1, 3].
Решение. (c помощью пакета Mathcad)
Обратимся теперь к теореме существования. Для исследуемой начальной задачи (3) функция f, определяемая равенством, определена и непрерывна во всей плоскости (x, y) за исключением точек оси абсцисс.
Таким образом, в соответствии с теоремой существования существует решение y(x) начальной задачи (3), определенное на некотором интервале, содержащем точку x0 = -1, и это решение по теореме о продолжении может быть продолжено до значения, близкого к значению y(x) = 0. В результате численного интегрирования получаем решение начальной задачи (3) на некотором интервале (a, b), где a < -1; 1,3 < b < 1,32. Однако, учитывая, что это уравнение с разделяющимися переменными, можно аналитически найти частное решение, удовлетворяющее начальной задаче (3)
Интегрируя, получаем, что
Отсюда следует, что решение начальной задачи (3) существует только для
Оказывается, обращение к теореме существования (и к теореме о продолжении) позволило отсечь отрезок (приблизительно [1,315; 5]), на котором решение исходной начальной задачи (3) заведомо не существует. Одно же только численное интегрирование приводит к ошибочному результату. Дело здесь в том, что при приближении решения y = y(x) к оси Ox угол наклона кривой приближается к 90°. Поэтому пока аргумент x изменяется на величину 0,1 значение y успевает перескочить ось Ox, и мы попадаем на интегральную кривую, отличную от исходной. А это происходит потому, что метод Эйлера учитывает угол наклона только в текущей точке.
Пример 2. Используя метод Эйлера, а затем метод Эйлера-Коши, с шагом h = 0,1 и итерационной схемой
,
где
,
решить начальную задачу
y(-1) = -1, (4)
на промежутке [-1, 1].
Решение. На базе Mathcad методом Эйлера, а затем методом Эйлера-Коши будем иметь:
Рис. 2
Получили чертеж (рис. 3) отличный от чертежа, изображенного на (рис. 2). Чтобы лучше разобраться в причине расхождения в результатах, проинтегрируем исходную начальную задачу. Разделяя переменные, имеем
или, окончательно, .
Становится понятно, что решение по методу Эйлера приближает функцию y1(x) = x3, а по улучшенному методу Эйлера - функцию
При этом как, y1 так и y2 являются решениями начальной задачи (4), а значит, для рассматриваемой на промежутке [-1; 1] начальной задачи имеет место неединственность.
Обращаясь теперь к теореме существования и единственности, отметим, что, так как функция f, заданная равенством, непрерывна во всей плоскости (x, y), то из теоремы существования следует, что существует решение начальной задачи (4), определенное на некотором промежутке, содержащем точку x0 = -1, и это решение по теореме о продолжении может быть продолжено на любой промежуток. Далее, поскольку
,
то функция
удовлетворяет условию Липшица по переменной y в любой области, не содержащей точки оси Ox. Если же область содержит точку оси Ox, то нетрудно показать, что в ней указанная выше функция условию Липшица не удовлетворяет. Поэтому из теоремы существования и единственности (и теоремы о продолжении) следует, что в данном случае решение начальной задачи может быть продолжено единственным образом, по крайней мере, до оси Ox. Но поскольку прямая y = 0 является особой интегральной прямой для дифференциального уравнения
,
то, как только y станет равным нулю решение начальной задачи (4) не может быть единственным образом продолжено за точку O(0, 0).
Рис. 3
Итак, обращение в данном случае к теореме существования и единственности (и теореме о продолжении) позволило разобраться в результатах численного интегрирования. Если речь идет о единственном на промежутке [-1; 1] решении начальной задачи (4), то оно существует и определено лишь на отрезке [-1; 0]. В общем же случае таких решений несколько.
Список литературы
1. Roberts C.E. Jr. Why teach existence and uniqueness theorems in the first course in ordinary differential equations? // Int. J. Math. Educ. Sci. Technol. - 1976. - Vol. 7, № 1. - P. 41-44.
Статья в формате PDF 123 KB...
23 04 2024 8:48:34
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
22 04 2024 23:33:33
21 04 2024 20:23:55
 Статья в формате PDF
164 KB...
Статья в формате PDF
164 KB...
19 04 2024 5:39:23
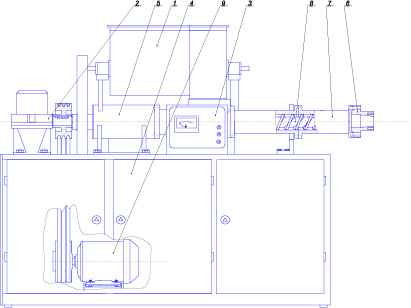 Проведены исследования в области экструдирования многокомпонентных смесей из отходов различных производств, предложена технологическая схема линии по получению ДПКТ. Экспериментальные исследования проводились в два этапа и определялись параметры процесса – производительность, мощность сил полезного сопротивления, в зависимости от угловой скорости вращения шнека пресса-экструдера, от температуры экструдируемого материала, от влажности экструдируемой смеси и процентного содержания компонентов смеси.
...
Проведены исследования в области экструдирования многокомпонентных смесей из отходов различных производств, предложена технологическая схема линии по получению ДПКТ. Экспериментальные исследования проводились в два этапа и определялись параметры процесса – производительность, мощность сил полезного сопротивления, в зависимости от угловой скорости вращения шнека пресса-экструдера, от температуры экструдируемого материала, от влажности экструдируемой смеси и процентного содержания компонентов смеси.
...
18 04 2024 12:54:52
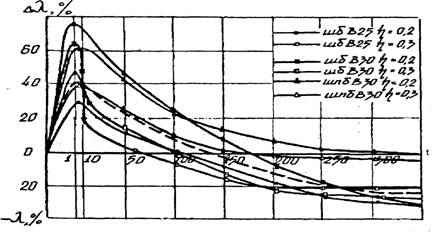 Основным механизмом теплообмена для капиллярно-пористых физических систем (типа легкого бетона) является контактная теплопроводность, которая осуществляется благодаря связанным между собой процессам: переходом тепла от частицы к частице через непосредственные контакты между ними и переходом тепла через разделяющую промежуточную среду. С термодинамической точки зрения теплообмен в легких бетонах представляет собой теплоперенос (поток тепла Q), а точнее перенос энтропии (S), под действием градиента температуры (Т), осуществляемый, в соответствии со вторым законом термодинамики, от мест с более высокой к местам с меньшей температурой. Термодинамическая идентичность коэффициента теплопроводности () и S позволила, на базе второго закона термодинамики, вывести общее уравнение для прогноза теплопроводности легкого бетона в условиях его эксплуатации. Установлено, что релаксация теплопроводности (τ) пропорциональна затуханию объемных деформаций бетона (Θ), вызванных температурным градиентом и уровнем напряжения (η). Экспериментальные исследования теплопроводности легкого бетона подтвердили затухающий хаpaктер изменения Δλ как функции времени (t) и деформативности.
...
Основным механизмом теплообмена для капиллярно-пористых физических систем (типа легкого бетона) является контактная теплопроводность, которая осуществляется благодаря связанным между собой процессам: переходом тепла от частицы к частице через непосредственные контакты между ними и переходом тепла через разделяющую промежуточную среду. С термодинамической точки зрения теплообмен в легких бетонах представляет собой теплоперенос (поток тепла Q), а точнее перенос энтропии (S), под действием градиента температуры (Т), осуществляемый, в соответствии со вторым законом термодинамики, от мест с более высокой к местам с меньшей температурой. Термодинамическая идентичность коэффициента теплопроводности () и S позволила, на базе второго закона термодинамики, вывести общее уравнение для прогноза теплопроводности легкого бетона в условиях его эксплуатации. Установлено, что релаксация теплопроводности (τ) пропорциональна затуханию объемных деформаций бетона (Θ), вызванных температурным градиентом и уровнем напряжения (η). Экспериментальные исследования теплопроводности легкого бетона подтвердили затухающий хаpaктер изменения Δλ как функции времени (t) и деформативности.
...
17 04 2024 23:59:22
 Статья в формате PDF
144 KB...
Статья в формате PDF
144 KB...
16 04 2024 20:59:43
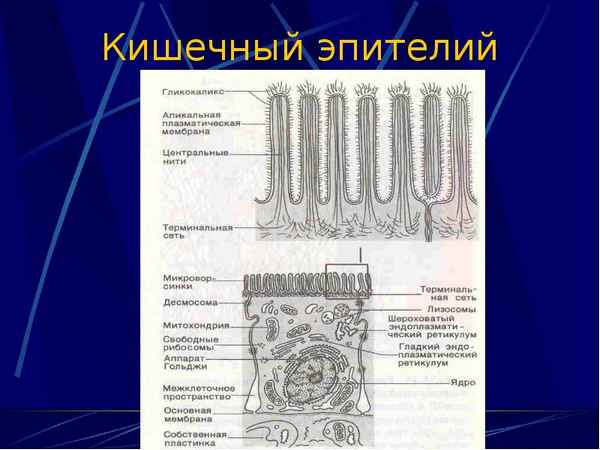
Изучено влияние трaнcкраниальной электростимуляции на слизистую оболочку желудка. Выделяемые при этом воздействии эндогенные нейропептиды влияют на морфометрические параметры слизистой и на темп синтеза эпителиоцитами муцинов. При интактной слизистой наблюдается эффект гиперплазии ее с увеличением в составе желез мукоцитов. В условиях нарушения статуса слизистой желудка введением цистеамина действие трaнcкраниальной стимуляции прослеживается в увеличении факторов резистентности слизистой. ...
15 04 2024 6:59:18
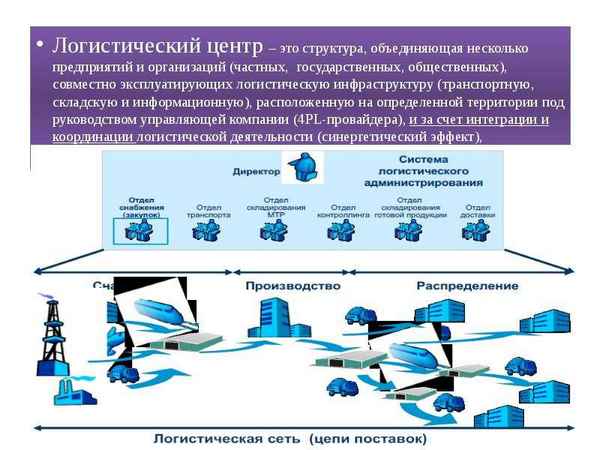 Статья в формате PDF
264 KB...
Статья в формате PDF
264 KB...
14 04 2024 10:34:47
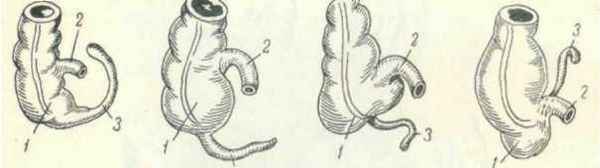 Слепая кишка белой крысы имеет форму изогнутого чаще вправо конуса или рога, илеоцекальный угол располагается по средней линии или рядом с нею. Реже полукольцевидная слепая кишка крысы находится влево от средней линии и петель подвздошной кишки.
...
Слепая кишка белой крысы имеет форму изогнутого чаще вправо конуса или рога, илеоцекальный угол располагается по средней линии или рядом с нею. Реже полукольцевидная слепая кишка крысы находится влево от средней линии и петель подвздошной кишки.
...
13 04 2024 0:18:39
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
12 04 2024 5:13:24
 Статья в формате PDF
130 KB...
Статья в формате PDF
130 KB...
11 04 2024 3:24:30
Статья в формате PDF 120 KB...
10 04 2024 0:30:16
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
09 04 2024 15:56:43
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
08 04 2024 8:37:22
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
07 04 2024 17:58:30
06 04 2024 21:17:47
05 04 2024 8:45:26
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
04 04 2024 8:32:41
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
03 04 2024 6:10:48
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
02 04 2024 1:12:41
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
01 04 2024 10:44:24
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
31 03 2024 5:44:47
 Статья в формате PDF
252 KB...
Статья в формате PDF
252 KB...
30 03 2024 12:37:20
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
29 03 2024 9:23:18
Статья в формате PDF 231 KB...
28 03 2024 0:54:12
 Статья в формате PDF
271 KB...
Статья в формате PDF
271 KB...
27 03 2024 13:49:44
 Статья в формате PDF
214 KB...
Статья в формате PDF
214 KB...
26 03 2024 5:50:29
 Статья в формате PDF
297 KB...
Статья в формате PDF
297 KB...
25 03 2024 22:32:38
 Статья в формате PDF
296 KB...
Статья в формате PDF
296 KB...
24 03 2024 22:24:22
 Статья в формате PDF
249 KB...
Статья в формате PDF
249 KB...
23 03 2024 20:31:58
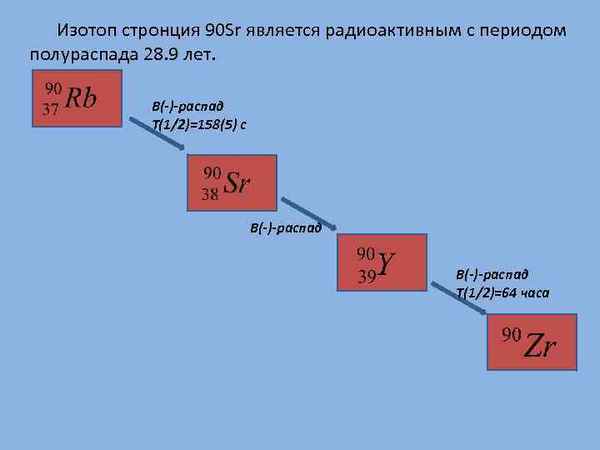 Приведены данные по концентрациям и соотношениям изтопов стронция и неодима в шошонитовых гранитоидах Алтае-Саянской складчатой области, Большого Кавказа, Британских каледонид, Шотландии, Западного Кунь-Луня, Бразилии. Выделены 4 подтипа гранитоидов, различающихся степенями изотопной обогощённости и деплетированности. По соотношениям 87Sr/86Sr отмечены широкие вариации значений от 0,7022 (мантийные значения) до 0,712958 (компонент обогащённой мантии c контаминацией корового материала). Все подтипы шошонитовых гранитоидов тяготеют к компонентам обогащённой мантии типов EM I и EM II. Это связывается с допущением о вовлечении в субдукционный процесс нижней части континентальной литосферы, или с субдуцированием в мантию терригенных осадков.
...
Приведены данные по концентрациям и соотношениям изтопов стронция и неодима в шошонитовых гранитоидах Алтае-Саянской складчатой области, Большого Кавказа, Британских каледонид, Шотландии, Западного Кунь-Луня, Бразилии. Выделены 4 подтипа гранитоидов, различающихся степенями изотопной обогощённости и деплетированности. По соотношениям 87Sr/86Sr отмечены широкие вариации значений от 0,7022 (мантийные значения) до 0,712958 (компонент обогащённой мантии c контаминацией корового материала). Все подтипы шошонитовых гранитоидов тяготеют к компонентам обогащённой мантии типов EM I и EM II. Это связывается с допущением о вовлечении в субдукционный процесс нижней части континентальной литосферы, или с субдуцированием в мантию терригенных осадков.
...
22 03 2024 0:50:18
 Статья в формате PDF
137 KB...
Статья в формате PDF
137 KB...
21 03 2024 5:32:18
 Статья в формате PDF
155 KB...
Статья в формате PDF
155 KB...
20 03 2024 14:56:14
 Статья в формате PDF
318 KB...
Статья в формате PDF
318 KB...
19 03 2024 22:34:40
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
18 03 2024 8:23:48
17 03 2024 4:13:38
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
16 03 2024 21:44:35
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
15 03 2024 5:45:18
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::