ИНТЕРВАЛЬНАЯ И НЕЧЕТКАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ ДЛЯ ВВП РОССИИ
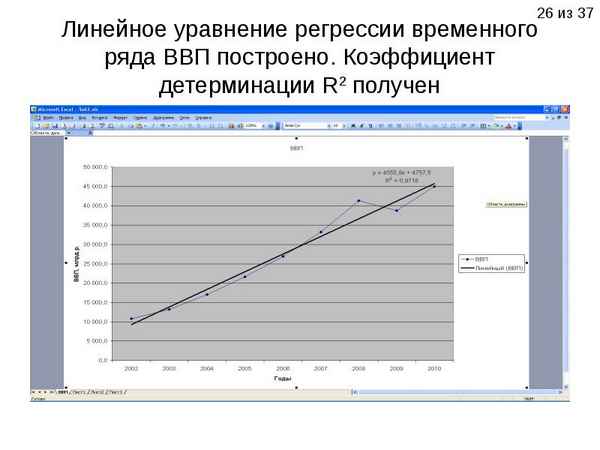
В соответствии с [1, 2] построим для промежутка времени 18 лет закон изменения в процентах валового внутреннего продукта Российской Федерации, отыскивая по методу наименьших квадратов параметры x 1 , x 2 этого закона, который прогнозируется в виде y = x 1 + x 2 z для моментов наблюдений z1 = 0 (год 1989), z2 =3 (год 1992), z3 = 4 (год 1993), ..., z16 = 17 (год 2006). Здесь многоточие обозначает zi = i+1 для i = 5,...,15... Предполагается, что для этих лет изменения в процентах ВВП было : y1 = 0, y2 = -18, y3 = -14, y4 = - 20, y5 = -3, y6 = -5, y7 = 2, y8 = -4, y9 = -2, y10 = 8, y 11 =5, y 12 = 4, y 13 = 6, y 14 = 4, y 15 = 5, y 16 = 6 (различные авторы предполагают изменение ВВП России в 2006 году от 5.9 процентов до 6.2). Вычисляя по формулам метода наименьших квадратов с использованием полиномов Чебышева [1], получим:
y = -13.3 + 1.2 z. (1)
Вычисляя по (1) теоретические значения величин ВВП yi = y(zi ), можем найти величины отклонений от измеренных значений yi-yi и определить окрестность стабильного развития России, которая приходится на последние 5 лет, что хорошо видно при графической интерпретации (1) и измерений. На промежутке стабильного развития наибольшее отклонение над прямой (для 2003 года) порождает реализацию yi2 = y i + 2.5, дающую по методу наименьших квадратов верхнюю границу окрестности стабильности
y = -10.8 + 1.2 z. (2)
Аналогичным образом наибольшее отклонение -1.1 под прямой (1) (для 2006 года) дает нижнюю границу промежутка стабильности
y= -14.4 + 1.2 z. (3)
Из (2), (3) имеем прогнозируемое значение ВВП в 2007 году (z=18) в виде интервального числа [8, 12]. Аналогично прогнозируемое значение ВВП в 2008 году будет [9, 13]. Прямая регрессии (1) даст для ВВП прогнозируемые значения для 2007, 2008 годов соответственно в виде 9 и 10 процентов, что позволит ввести [3] треугольные нечеткие числа [8, 9,12] для ВВП в 2007 году и [9, 10, 13] для ВВП в 2007 году, которые являются нечеткими подмножествами соответствующих им интервальных чисел [2].
СПИСОК ЛИТЕРАТУРЫ:
- Тарушкин В.Т., Тарушкин П.В., Тарушкина Л.Т. Интервальное решение задачи Д.И. Менделеева - А.А. Маркова - Ю.В. Линника. Электронная конференция РАЕН "Современные проблемы науки и образования", 15 - 20 ноября 2006.
- Тарушкин В.Т., Тарушкин П.В., Тарушкина Л.Т. Нечеткие решения задачи Д.И. Менделеева - А.А. Маркова - Ю.В. Линника. Электронная конференция РАЕН "Современные проблемы науки и образования", 15 - 20 декабря 2006.
- Тарушкин В.Т. Интервальный и нечеткий методы наименьших квадратов. Всероссийское (с международным участием) совещание по интервальному анализу и его приложениям "Интервал - 06", c. 119 - 121, CПб, 2006.
Статья в формате PDF
245 KB...
25 04 2024 19:57:16
Статья в формате PDF 231 KB...
24 04 2024 5:42:54
Статья в формате PDF
110 KB...
23 04 2024 6:40:21
Статья в формате PDF
225 KB...
22 04 2024 13:34:35
Статья в формате PDF
123 KB...
21 04 2024 6:35:17
Статья в формате PDF
114 KB...
20 04 2024 3:16:16
Явная неопределенность поведения сферы образования вызывает значимые риски. Во многом они связаны с самими экспертами и их группами, имеющими свои корпоративные интересы. Факторы риска промоделированы по статистическим данным идентификацией устойчивых закономерностей в виде тенденций (трендов) и показана методика анализа. Даны рейтинговые места экспертным оценкам. Анализ закономерностей показал, что в России нужно повышать чувствительность экспертов к реальной действительности, а также к адекватному представлению сценариев долгосрочной перспективы развития. Пока не будет результатов в реформах образования, нечего ждать и формирования инновационной экономики. Ведь из мировой пpaктики известно, цикл пассионарной активности опережает цикл экономического возрождения на 3–5 лет.
...
19 04 2024 15:44:17
Статья в формате PDF
105 KB...
17 04 2024 1:37:56
Статья в формате PDF
265 KB...
16 04 2024 7:12:45
Статья в формате PDF
107 KB...
15 04 2024 23:47:42
Статья в формате PDF
284 KB...
14 04 2024 15:32:34
Статья в формате PDF
112 KB...
13 04 2024 19:59:25
Статья в формате PDF
106 KB...
12 04 2024 17:51:21
Статья в формате PDF
134 KB...
10 04 2024 6:30:59
Статья в формате PDF
113 KB...
09 04 2024 6:40:23
Статья в формате PDF
141 KB...
07 04 2024 4:46:40
Статья в формате PDF
273 KB...
06 04 2024 3:26:34
Статья в формате PDF
261 KB...
05 04 2024 15:48:54
Статья в формате PDF
107 KB...
03 04 2024 6:57:31
Статья в формате PDF
99 KB...
01 04 2024 0:59:28
Статья в формате PDF
105 KB...
31 03 2024 5:50:57
Статья в формате PDF
58 KB...
30 03 2024 15:47:44
В данной статье осуществлены анализ и обощение зарубежных психологических концепций, объясняющих активность человека в отношении своего здоровья, и на этой основе дано авторское определение понятия «здоровьесозидающий потенциал личности». Особое внимание авторы уделяют рассмотрению структуры здоровьесозидающего потенциала, описанию психологических механизмов его формирования и выявлению закономерностей его развития в различные возрастные периоды. Авторами впервые представлена и научно обоснована векторная модель здоровьесозидающего потенциала личности, показаны её возможности при выявлении психологических детерминант, влияющих на показатели целостного здоровья человека.
...
29 03 2024 15:12:43
В настоящее время важно пройти сложнейший этап перехода к новому типу социально-экономического развития быстро, компетентно, опираясь на собственные творческие возможности.
Именно этим целям служит разработанная нами модель педагогических основ формирования целостного образовательного прострaнcтва, основу которого составляет внедрение непрерывного образования в интегрированном профессиональном учебном заведении.
Моделирование целостного образовательного прострaнcтва осуществлялось нами через уточнение таких понятий, как «интеграция», «межпредметные связи», «взаимосвязь», интегративно-педагогические закономерности, интегративная деятельность, через изучение опыта зарубежных исследователей, решающих проблемы педагогической интеграции.
...
28 03 2024 20:22:22
Статья в формате PDF
142 KB...
27 03 2024 20:48:17
Статья в формате PDF
112 KB...
26 03 2024 3:12:37
Статья в формате PDF
157 KB...
25 03 2024 5:57:14
Статья в формате PDF
120 KB...
24 03 2024 5:22:27
Статья в формате PDF
217 KB...
22 03 2024 21:32:46
Статья в формате PDF
263 KB...
21 03 2024 2:13:48
Статья в формате PDF
100 KB...
20 03 2024 10:32:39
Статья в формате PDF
103 KB...
19 03 2024 18:44:47
Рассмотрены некоторые проблемы идентификации моделей распределения данных, при использовании современного математического аппарата для решения этой задачи. Показано, что использование методов нелинейной оптимизации для идентификации моделей приводит к улучшению результатов идентификации, но одновременно, изменяет формальную постановку задачи. Выделено три группы проблем, связанных с выбором критериев согласия, их критических значений и проверкой адекватности получаемых моделей. Проанализированы возможные подходы к решению этих проблем.
...
17 03 2024 19:44:42
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
