РАСЧЕТ СОСТАВНОЙ КОНСТРУКЦИИ С ОДНОСТОРОННИМИ ВНУТРЕННИМИ СВЯЗЯМИ В СРЕДЕ MATHCAD
Рассматривается равновесие составной конструкции (рис. 1), имеющей внутренние односторонние связи в точках Е и F [1]. Требуется:
1) выяснить, какая из связей работает, т.е. в какой из точек Е или F при заданной нагрузке имеет место контакт (на рисунке показаны зазоры в обоих случаях), а также определить реакции связей;
2) определить область значений угла a, в точках которой RE > 0, и область значений этого угла, в точках которой RF > 0.
Рис. 1
Предполагая, что контакт осуществляется в точке E, расчлeняем конструкцию на составляющие ее тела AC, CD, EFDL и рассматриваем равновесие каждого тела отдельно; при этом действие связей заменяем их реакциями. На каждое тело действует уравновешенная плоская система сил. Расчетная схема для тела AC приведена на рис. 2.
Рис. 2
Уравнения равновесия сил, действующих на тело CD, имеют вид:
(1)
Расчетная схема для тела CD приведена на рис. 3. Заметим, что .
Рис. 3
Уравнения равновесия сил, действующих на тело CD, имеют вид:
(2)
Расчетная схема для тела EFDL приведена на рис. 4. Заметим, что , .
Уравнения равновесия сил, действующих на тело CD, имеют вид:
(3)
Рис. 4
Из системы девяти уравнений (1)-(3) можно определить неизвестные реакции связей RE, XA, YA, RB, XC, YC, XD, YD, RL.
Аналогичнопредполагая, что контакт осуществляется в точке F, получаем систему уравнений для определения реакций связей RF, XA, YA, RB, XC, YC, XD, YD и RL и (эта система здесь не приводится).
Решение полученных систем линейных уравнений проводилось в среде Mathcad. Использовался метод обратной матрицы. Расчеты показывают, что при заданных нагрузках контакт имеет место в точке E, так RE > 0.
Определим область значений угла α при условии RE > 0. Для этого воспользуемся принципом возможных перемещений. Предполагая, что контакт осуществляется в точке E, освободим конструкцию от связи в этой точке, заменив ее действие реакциями и . Полученный плоский механизм имеет одну степень свободы. Звено AC этого механизма может вращаться вокруг неподвижного центра A, а звенья EFDL и CD - совершать плоское движение. Сообщим звену AC возможное перемещение δφ1 (рис. 5). Возможным перемещением звена CD является поворот на угол δφ2 вокруг мгновенного центра вращения P2, а возможным перемещением звена EFDL- поворот на угол δφ3 вокруг мгновенного центра вращения P3. Центр P3 найден как точка пересечения перпендикуляров к направлениям возможных перемещений точек B и L, а центр P2 - как точка пересечения перпендикуляров к направлениям возможных перемещений точек C и D.
Рис.5
Записывая уравнение работ принципа возможных перемещений, получаем
(4)
Учитывая, что
из уравнения (4) находим
(5)
Аналогично, полагая, что контакт осуществляется в точке F, находим
(6)
Располагая формулами (5) и (6) (вообще говоря, достаточно одной из них) можно найти области значений угла a на отрезке [-π, π] в точках которых выполняются неравенства RE > 0 или RF > 0. Расчет проводился в среде Mathcad. Построены графики функций RE(a) и RF(a). Корни уравнений RE(a) = 0 и RF(a) = 0 на отрезке [-π, π] определены с помощью функции-процедуры root.
Список литературы
- Сборник заданий для курсовых работ по теоретической механике / под ред. А.А. Яблонского. - М.: Высшая школа - 1985.
- Кирьянов Д. В. Самоучитель Mathcad 11. - СПб.: БХВ-Петербург - 2003.
Статья в формате PDF
111 KB...
24 04 2024 23:40:14
Статья в формате PDF
147 KB...
23 04 2024 3:25:10
Статья в формате PDF
103 KB...
22 04 2024 12:42:12
Статья в формате PDF
255 KB...
21 04 2024 13:34:57
Статья в формате PDF
155 KB...
19 04 2024 8:55:35
Статья в формате PDF
110 KB...
18 04 2024 19:41:31
Статья в формате PDF
267 KB...
17 04 2024 23:11:58
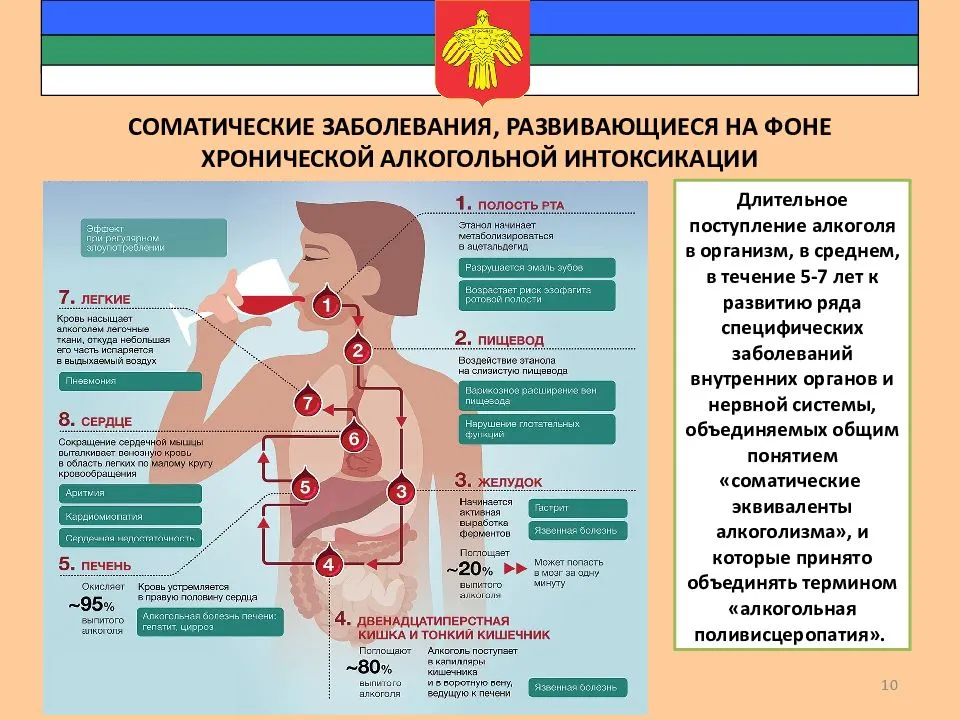Статья посвящена актуальной проблеме – влиянию хронической алкогольной интоксикации на изменение структуры капсулы селезенки в раннем постнатальном онтогенезе. Дана сравнительная гистологическая хаpaктеристика капсулы с учетом зависимости изменений от различной концентрации потрeбляемого алкоголя.
...
16 04 2024 17:41:40
Статья в формате PDF
102 KB...
14 04 2024 19:13:47
Статья в формате PDF
127 KB...
13 04 2024 8:49:15
Статья в формате PDF
284 KB...
12 04 2024 8:28:43
Статья в формате PDF
161 KB...
11 04 2024 4:54:16
Статья в формате PDF
103 KB...
10 04 2024 8:54:29
Статья в формате PDF
190 KB...
09 04 2024 1:39:33
Статья в формате PDF
282 KB...
08 04 2024 21:48:44
Статья в формате PDF
94 KB...
07 04 2024 3:30:20
Статья в формате PDF
141 KB...
06 04 2024 15:42:42
Статья в формате PDF
106 KB...
05 04 2024 0:15:13
Статья в формате PDF
106 KB...
04 04 2024 12:42:11
Статья в формате PDF
329 KB...
03 04 2024 17:58:51
Статья в формате PDF
140 KB...
02 04 2024 21:32:41
Статья в формате PDF
117 KB...
01 04 2024 22:41:25
Статья в формате PDF
113 KB...
31 03 2024 2:52:55
Статья в формате PDF
109 KB...
30 03 2024 23:10:40
Статья в формате PDF
113 KB...
28 03 2024 13:12:14
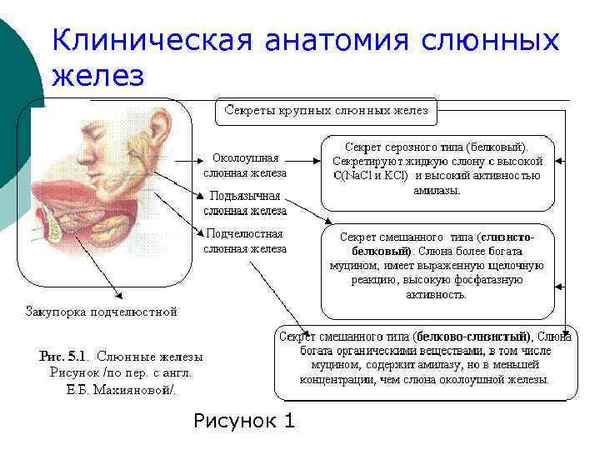С использованием метода газоразрядной визуализации (ГРВ) проведено исследование секретов околоушных, подчелюстных и подъязычных больших слюнных желез у 20 больных 2 типом сахарного диабета и 14 пpaктически здоровых людей. Выявлено, что параметры ГРВ-грамм секретов больших слюнных желез у пациентов с сахарным диабетом существенно ниже, чем у относительно здоровых лиц (p ...
27 03 2024 5:38:49
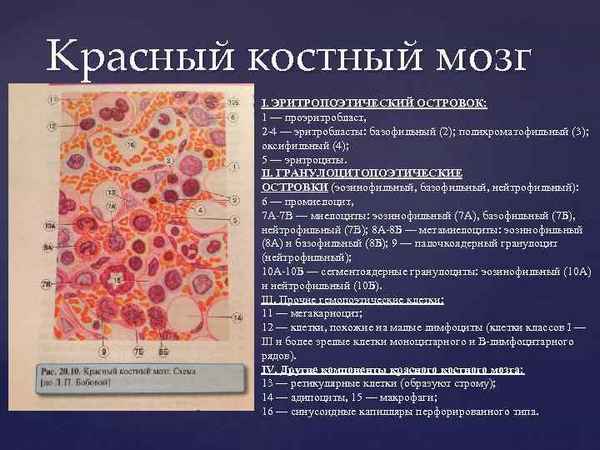Проведено исследование хаpaктера образования эритроклазических костномозговых кластеров при лихорадке у лабораторных животных. Установлено, что лихорадка сопровождается увеличением клеточности костного мозга, активацией эритроклазического кластерообразования нейтрофильными миелокариоцитами и макрофагами, сопровождающегося усилением экзоцитарного лизиса эритроцитов в кластерах, то есть увеличением цитолитической активности данных миелокариоцитов.
...
25 03 2024 4:28:17
Статья в формате PDF
104 KB...
24 03 2024 0:12:40
Статья в формате PDF
182 KB...
23 03 2024 0:39:23
Статья в формате PDF
274 KB...
22 03 2024 8:44:46
Статья в формате PDF
117 KB...
21 03 2024 10:28:48
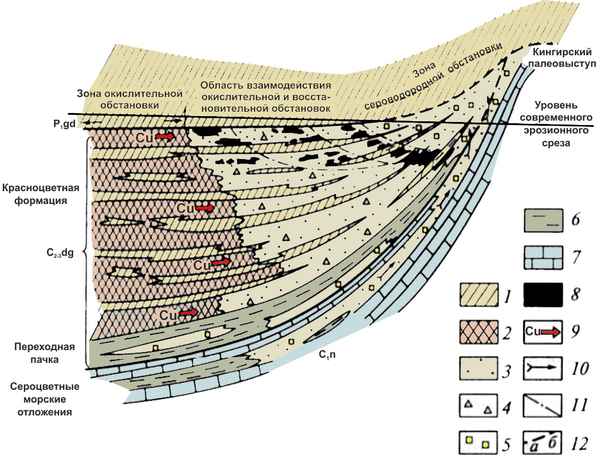Предложены принципы подбора целевых пород, рекомендуемых для выращивания при рекультивации земель в условиях Олюторского района Камчатского края.
...
20 03 2024 12:39:46
Статья в формате PDF
113 KB...
19 03 2024 22:48:34
Статья в формате PDF
313 KB...
18 03 2024 15:30:41
Статья в формате PDF
156 KB...
17 03 2024 22:10:56
Статья в формате PDF
169 KB...
16 03 2024 3:43:58
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
