КОНТРОЛЬ ЧИСЛЕННОСТИ ВОДНЫХ ОБИТАТЕЛЕЙ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Рассмотрим математическую модель совместного существования двух биологических видов типа «хищник- жертва», называемую моделью Лотки- Вольтера. Пусть есть двабиологических вида, которые совместно обитают визолированной среде. Будем дляопределенности называть ихкарасями ищуками. Караси ищуки живут внекотором изолированном пруду. Среда предоставляет карасям питание внеограниченном количестве, ащуки питаются лишь карасями. Обозначим: у- число щук, х- число карасей.
Со временем число карасей ищук меняется, нотак какрыбы впруду много, тоне будем различать 1020 карасей или1021 ипоэтому будем считать хи унепрерывными функциями времени t. Будем называть пару чисел (х,у) состоянием модели. Рассмотрим, какменяется состояние (х, у) стечением времени. Пусть x’- скорость изменения численности карасей. Если щукнет, точисло карасей увеличивается итем быстрее, чембольше карасей. Будем считать, чтоэта зависимость линейная : x’ ~ε1 x, причем коэффициент ε1 зависит только отусловий жизни карасей, ихестественной cмepтности ирождаемости. Скорость изменения y’ числа щук(если неткарасей), зависит отчисла щукy. Будем считать, чтоy’~ε2 y, если карасей нет, точисло щукуменьшается (у нихнет пищи) иони вымирают. Вэкосистеме скорость изменения численности каждого вида пропорциональной егочисленности, нотолько скоэффициентом, который зависит отчисленности особей другого вида.
Так, длякарасей этот коэффициент уменьшается сувеличением числа щук, адля щукувеличивается сувеличением числа карасей. Будем считать этузависимость также линейной. Тогда получим систему издвух дифференциальных уравнений: x’ = ε1 x- γ1yx, y’ = -ε2 y+ γ2 xy.
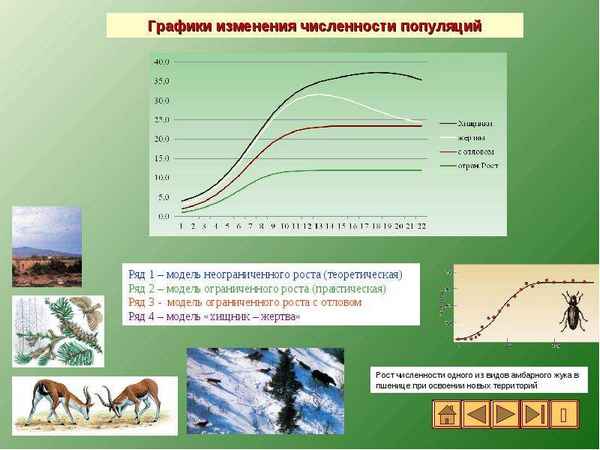
Эта система уравнений иназывается моделью Вольтерра-Лотки. Числовые коэффициенты ε1, γ1, ε2, γ2 называются параметрами модели. Очевидно, чтохаpaктер изменения состояния (x, y) определяется значениями параметров. Изменяя параметры ирешая систему уравнений модели можно исследовать закономерности изменения состояния экологической системы. Именно этопозволит вамсделать наша модель, которая находит решение уравнения Вольтерра- Лотки ивыводит кривые x(t) иy(t) награфик. Вкачестве примера нарисунке построены кривые изменения численности карасей xи щукy взависимости отвремени tдля некоторых типичных значений параметров. Максимумы кривых чередуются, причем максимумы щукотстают отмаксимума карасей. Этоотставание разное дляразных экосистем типа «хищник- жертва», но, какправило, много меньше периода колебаний.
В таблице показаны прогнозируемые результаты, полученные нами припомощи изученной модели. Этоколичество разведенной рыбы вКарельском водохранилище, приучете, чтопо нормам рыбоводства наодну тонну хищников приходится 2,5 тонны жертв.
|
2000 год |
2005 год |
2009 год |
|
|
Количество хищных рыб(т) |
16 |
18 |
17,5 |
|
Количество кормовых рыб(т) |
42 |
47,25 |
46 |
Статья в формате PDF
112 KB...
18 04 2024 21:49:22
Статья в формате PDF
114 KB...
17 04 2024 15:11:45
Статья в формате PDF
120 KB...
16 04 2024 19:52:51
Изучено состояние процесса перекисного окисления липидов и антиокислительной системы в различных участках миокарда при его инфаркте у крыс с разной резистентностью к гипоксии. Выявлено что, в норме активность перекисного окисления липидов несколько выше у высокоустойчивых к гипоксии крыс по сравнению с низкоустойчивыми, однако активность антиокислительных ферментов, наоборот, выше у высокоустойчивых крыс. При коронароокклюзии интенсивность перекисного окисления липидов существенно повышается у низкоустойчивых к гипоксии крыс.
...
13 04 2024 22:23:45
Статья в формате PDF
101 KB...
12 04 2024 14:29:22
Статья в формате PDF
95 KB...
11 04 2024 21:33:21
Статья в формате PDF
124 KB...
10 04 2024 23:49:38
Статья в формате PDF
152 KB...
09 04 2024 7:53:46
Статья в формате PDF
261 KB...
08 04 2024 23:17:38
Статья в формате PDF
146 KB...
07 04 2024 20:23:13
Статья в формате PDF
173 KB...
06 04 2024 22:10:51
Статья в формате PDF
108 KB...
05 04 2024 20:28:48
Статья в формате PDF
109 KB...
04 04 2024 7:44:40
Статья в формате PDF
109 KB...
03 04 2024 14:51:56
Статья в формате PDF
174 KB...
02 04 2024 0:29:18
Статья в формате PDF
272 KB...
01 04 2024 14:15:56
Статья в формате PDF
128 KB...
31 03 2024 20:16:39
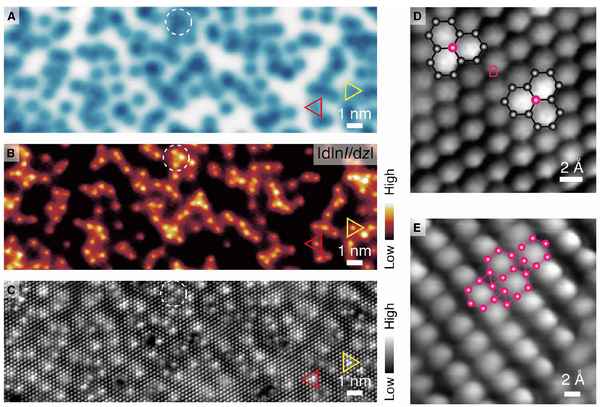В данной работе предложена эволюционная модель формирования двумерных структур. Определены алгоритмы формирования структур в априори структурированном двумерном прострaнcтве путем заполнения его в соответствии с определенными эволюционными правилами.
...
30 03 2024 11:11:59
Статья в формате PDF
112 KB...
29 03 2024 17:33:30
Статья в формате PDF
135 KB...
28 03 2024 20:40:30
Статья в формате PDF
147 KB...
27 03 2024 10:52:32
Статья в формате PDF
113 KB...
26 03 2024 2:59:15
Статья в формате PDF
107 KB...
25 03 2024 15:18:32
Статья в формате PDF
128 KB...
24 03 2024 5:49:50
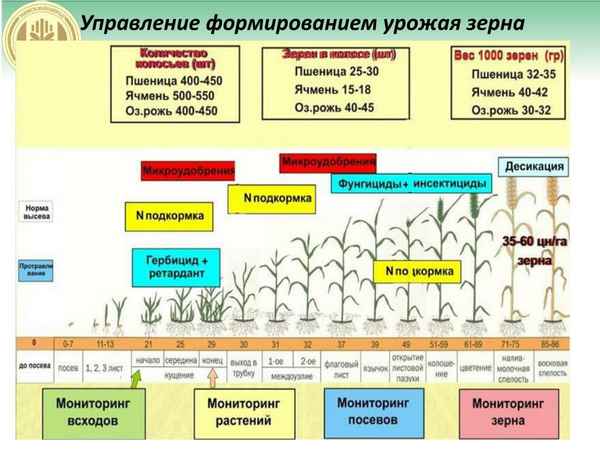Установлено, что применение биопрепаратов биогумус, гуми и альбит при замачивании семян и некорневой подкормке раннеспелых гибридов огурца в пленочной теплице, положительно влияют на энергию прорастания и всхожесть семян, ускоряют рост и развитие растений огурца, сокращают межфазный период на 3- 4 дня, вегетационный период, на 5-6 дней. Благоприятно влияют на водный режим растений, увеличение ассимиляционной поверхности, фотосинтетический потенциал и урожайность. Наиболее эффективное действие оказывали биопрепараты биогумус и гумми на гибридах, отечественной селекции Арина и голландской Машенька.
...
23 03 2024 8:35:23
Статья в формате PDF
131 KB...
22 03 2024 21:19:57
Статья в формате PDF
236 KB...
21 03 2024 7:15:37
Статья в формате PDF
112 KB...
20 03 2024 2:20:52
Статья в формате PDF
279 KB...
19 03 2024 23:58:48
Статья в формате PDF
133 KB...
18 03 2024 23:31:57
Статья в формате PDF
323 KB...
17 03 2024 18:36:12
Статья в формате PDF
102 KB...
16 03 2024 3:59:31
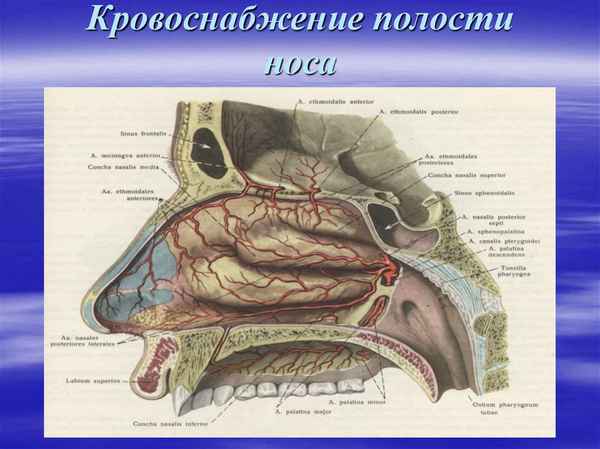В статье приведены современные данные о микроанатомии и гистологии слизистой оболочки полости носа. Приводятся особенности морфо-функциональной организации носа в связи с зональными особенностями, сравнителая хаpaктеристика различных отделов носовой полости. Представлено клиническое значение вариантов анатомической организации структур носа с различными видами ринопатологии.
...
15 03 2024 18:23:48
Статья в формате PDF
208 KB...
14 03 2024 22:20:58
Статья в формате PDF
115 KB...
13 03 2024 5:25:45
Статья в формате PDF
118 KB...
12 03 2024 19:56:51
Статья в формате PDF
314 KB...
11 03 2024 8:14:38
Статья в формате PDF 279 KB...
10 03 2024 8:39:30
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::
