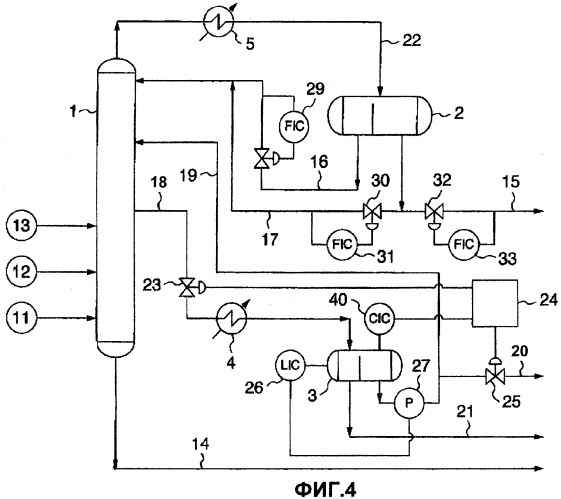
ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ ПАРНОЙ РЕГРЕССИИ ОТ ПАРАМЕТРОВ ФУНКЦИИ ВЕЙЕРШТРАССА-МАНДЕЛЬБРОТА ПРИ МОДЕЛИРОВАНИИ СРЕДНЕГО ЗНАЧЕНИЯ ФУНКЦИИ С ПОМОЩЬЮ ЕЕ ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ

Введение
При моделировании микроускорений с помощью действительной части фpaктальной функции Вейерштрасса-Maндельброта (ФВМ) [1]:
(1)
важно грамотно провести отождествление параметров функции (1) и реальных условий процесса возникновения поля микроускорений внутри КА.
Рисунок 1. Динамика изменения среднего значения ФВМ
Этой теме, равно как и возможности использовании ФВМ в виде (1) при тождественно равной нулю случайной фазе, посвящен ряд работ [2-5], с которыми можно ознакомиться для понимания решаемой задачи. В работе [4] были получены корреляционные зависимости между средним значением ФВМ (1) и фpaктальной размерностью D (рис. 1).
Как видно из рис. 1, они пpaктически линейны. Этот факт доказывается с помощью коэффициента детерминации, который при оценке качества моделирования корреляционных зависимостей рис. 1 во всех случаях превышает 0,999 (рис. 2).
Как видно из рис. 1, они пpaктически линейны. Этот факт доказывается с помощью коэффициента детерминации, который при оценке качества моделирования корреляционных зависимостей рис. 1 во всех случаях превышает 0,999 (рис. 2).
Рисунок 2. Зависимость коэффициента детерминации от параметра b при моделировании корреляционных зависимостей рис.1 линейной моделью парной регрессии
Постановка задачи
Для построения функциональной зависимости между фpaктальной размерностью ФВМ D и средним значением ФВМ (1) с помощью линейной модели парной регрессии вида:
(2)
требуется исследовать влияние параметра b ФВМ на коэффициенты и правой части (2), исходя из полученных ранее корреляционных зависимостей рис. 1.
Основные результаты работы
Как видно из рис. 1, оба исследуемых коэффициента с ростом b изменяются. Для аппроксимации корреляционной зависимости и b (рис. 3)
Рисунок 3. Корреляционная зависимость коэффициента а1 от параметра b
Была сначала построена линейная модель:
(3)
и с помощью метода наименьших квадратов (МНК) оценены коэффициенты и , которые получились равными: ; . Таким образом, наилучшая с точки зрения МНК линейная зависимость коэффициента от b имеет вид:
(4)
Затем была предпринята попытка улучшить качество аппроксимации за счет учета квадратичного члeна, заменив зависимость (3) на квадратичную вида:
, (5)
для которой также с помощью МНК были оценены коэффициенты: ; ; . Таким образом, наилучшая с точки зрения МНК квадратичная зависимость коэффициента от b имеет вид:
(6)
И, наконец, был произведен учет кубического члeна с помощью зависимости:
, (7)
При этом коэффициенты, найденные с помощью МНК, оказались равными: ; ; ; .
Таким образом, наилучшая с точки зрения МНК кубическая зависимость коэффициента от b имеет вид:
(8)
Качество построенных зависимостей (4), (6) и (8) проверялось с помощью коэффициента детерминации (рис. 4) и критерия согласия -Пирсона (рис. 5).
Рисунок 4. Изменение коэффициента детерминации при усложнении формы модели зависимости коэффициента а1 от параметра b
Усложнение модели связано, прежде всего с высоким качеством аппроксимации корреляционных зависимостей рис. 1 моделью (2). Значения коэффициентов детерминации для линейной и квадратичной моделей составили 0,979 и 0,998 соответственно, что ниже значений коэффициентов детерминации, рассчитанных при моделировании (рис. 2). И только модель (8) позволяет с уверенностью сделать вывод о том, что потерь качества при замене коэффициента на правую часть (8) не будет, т.к. значение коэффициента детерминации составляет 0,9995.
Рисунок 5. Динамика изменения наблюдаемого значения критерия согласия при усложнении модели
Критерий согласия еще более наглядно показывает улучшение качества моделирования при усложнении формы модели. Критическое значение критерия для рассматриваемых двух степеней свободы равно 5,99147 (5 %-й уровень значимости). Наблюдаемое значение критерия для линейной модели (4) составляет 5,613, что очень близко к критическому, несмотря на высокое значение коэффициента детерминации. Для квадратичной модели (6) величина наблюдаемого значения критерия сокращается более, чем в десять раз: 0,505 и почти в четыре раза сокращается еще для кубической модели (8): 0,130.
Таким образом, проверка качества построенных моделей (4), (6) и (8) показала, что лишь последняя из них достаточно точно описывает динамику изменения коэффициента в модели (2).
Следующим этапом является исследование зависимости другого параметра модели (2) от b. При замене корреляционных зависимостей рис.1 на функциональные вида (2) была построена зависимость изменения при различных значениях b. Эта зависимость приведена на рис. 6.
Рисунок 6. Корреляционная зависимость коэффициента а0 от параметра b
Аналогично схеме построения зависимости от b, сначала была исследована линейная зависимость, подобная (3). С помощью МНК подобраны коэффициенты этой модели:
(9)
Затем были подобраны лучшие с точки зрения МНК коэффициенты квадратичной зависимости, подобной (5):
(10)
и кубической зависимости, подобной (7):
(11)
Качество построенных моделей (9), (10) и (11) оценивалось с помощью коэффициента детерминации (рис. 7) и критерия согласия -Пирсона (рис. 8).
Рисунок 7. Изменение коэффициента детерминации при усложнении формы модели зависимости коэффициента а0 от параметра b
Рисунок 8. Динамика изменения наблюдаемого значения критерия согласия при усложнении модели
Таким образом, в результате данной работы построена модель зависимости среднего значения ФВМ от параметров функции:
Причем, данная модель объясняет более 99,9% дисперсии корреляционных зависимостей рис.
СПИСОК ЛИТЕРАТУРЫ
- Седельников А.В., Бязина А.В., Антипов Н.Ю. Использование функции Вейерштрасса-Maндельброта для моделирования микроускорений на борту КА //Сборник научных трудов X Всероссийского научно-технического семинара по управлению движением и навигации ЛА. Самара. 2002. с. 124-128.
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Анализ влияния параметров функции Вейерштрасса-Maндельброта на ее закон распределения //Современные наукоемкие технологии. - 2005 г. - № 9. - с. 43-46.
- Седельников А.В., Бязина А.В., Иванова С.А. Статистические исследования микроускорений при наличии слабого демпфирования колебаний упругих элементов КА //Научные чтения в Самарском филиале РАО. - Часть 1. Естествознание. - М.: Изд. УРАО. - 2003. - 137 - 158.
- Седельников А.В., Корунтяева С.С., Подлеснова Д.П. Исследование динамики изменения среднего значения фpaктальной функции Вейерштрасса-Maндельброта как случайной величины //Фундаментальные исследования. - № 4. - 2006. - с. 84-87.
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Выявление коридора значений параметров фpaктальной функции Вейерштрасса-Maндельброта, при которых справедлив нормальный закон распределения функции //Современные наукоемкие технологии. - № 1. - 2006. - с. 85-87.
 Статья в формате PDF
170 KB...
Статья в формате PDF
170 KB...
24 04 2024 7:17:24
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
23 04 2024 12:39:32
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
22 04 2024 11:28:56
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
21 04 2024 15:31:55
 Статья в формате PDF
161 KB...
Статья в формате PDF
161 KB...
20 04 2024 21:10:10
Статья в формате PDF 115 KB...
19 04 2024 9:31:28
18 04 2024 17:48:29
 Статья в формате PDF
544 KB...
Статья в формате PDF
544 KB...
15 04 2024 8:45:41
 Статья в формате PDF
136 KB...
Статья в формате PDF
136 KB...
14 04 2024 2:40:45
 Статья в формате PDF
215 KB...
Статья в формате PDF
215 KB...
13 04 2024 17:57:31
 Статья в формате PDF
184 KB...
Статья в формате PDF
184 KB...
12 04 2024 11:25:33
 В работе отражены особенности современных компьютерных и мехатронных технологий в дизайне изделий, способствующих повышению их потребительской ценности.
Раскрыта сущность и методология процесса машинного орнаментирования изделий.
...
В работе отражены особенности современных компьютерных и мехатронных технологий в дизайне изделий, способствующих повышению их потребительской ценности.
Раскрыта сущность и методология процесса машинного орнаментирования изделий.
...
11 04 2024 20:22:16
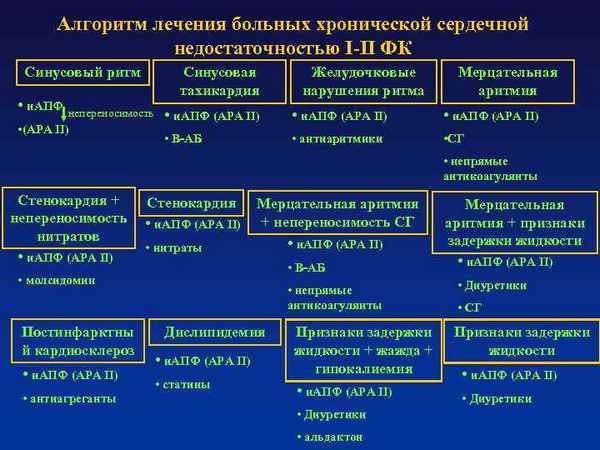 В статье описываются математические модели в виде уравнения регрессии, которое позволяет по клиническим признакам хронической сердечной недостаточности со статистической достоверностью предсказать результаты 6-минутного теста.
...
В статье описываются математические модели в виде уравнения регрессии, которое позволяет по клиническим признакам хронической сердечной недостаточности со статистической достоверностью предсказать результаты 6-минутного теста.
...
10 04 2024 14:49:35
 Статья в формате PDF
302 KB...
Статья в формате PDF
302 KB...
09 04 2024 22:46:13
 Статья в формате PDF
142 KB...
Статья в формате PDF
142 KB...
08 04 2024 11:14:34
 Статья в формате PDF
323 KB...
Статья в формате PDF
323 KB...
07 04 2024 23:40:48
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
06 04 2024 9:44:44
 Статья в формате PDF
313 KB...
Статья в формате PDF
313 KB...
05 04 2024 19:47:32
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
04 04 2024 5:54:26
 Статья в формате PDF
274 KB...
Статья в формате PDF
274 KB...
03 04 2024 9:19:46
 Статья в формате PDF
123 KB...
Статья в формате PDF
123 KB...
01 04 2024 17:57:53
 Информационное поле живой матери создается природой, природа адаптирует это поле, обучает окружающему мирозданию и формирует, передает, самоорганизующейся живой материи.
...
Информационное поле живой матери создается природой, природа адаптирует это поле, обучает окружающему мирозданию и формирует, передает, самоорганизующейся живой материи.
...
30 03 2024 12:29:10
 Предпочитающие алкоголь крысы при исследовании поведения в тестах «открытое поле» и «приподнятый крестообразный лабиринт» показали значимо большую двигательную активность и признаки повышенной тревожности. Содержание дофамина и норадреналина в миндалевидном комплексе мозга предпочитающих алкоголь крыс значимо выше, у них также ускорен метаболизм дофамина по сравнению с не предпочитающими алкоголь крысами.
...
Предпочитающие алкоголь крысы при исследовании поведения в тестах «открытое поле» и «приподнятый крестообразный лабиринт» показали значимо большую двигательную активность и признаки повышенной тревожности. Содержание дофамина и норадреналина в миндалевидном комплексе мозга предпочитающих алкоголь крыс значимо выше, у них также ускорен метаболизм дофамина по сравнению с не предпочитающими алкоголь крысами.
...
29 03 2024 15:45:35
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
28 03 2024 13:43:10
27 03 2024 1:41:41
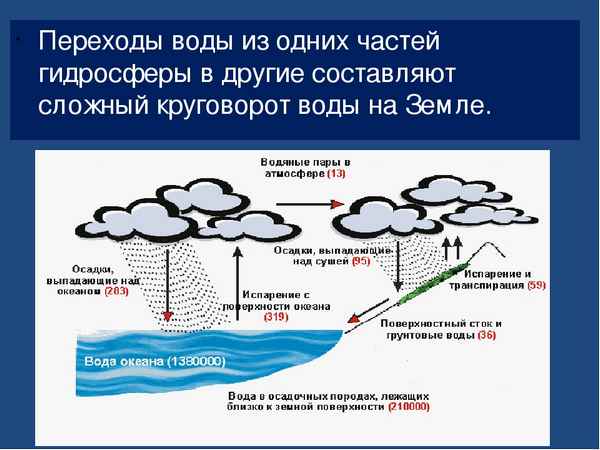
Анализ полученных результатов мониторинга воды Волго – Каспийского бассейна показал, что: уровень мутагенной активности загрязнений природных волжских вод достигает наибольшего значение в летний период; наиболее напряженная эколого- генетическая ситуация складывается в районах р. Бузан и г. Нариманов, находящихся в непосредственной близости от Газопереpaбатывающего завода; показатель уровня мутагенности водной среды с 1998 по 2001 г. незначительно снизился, но превышает предельно допустимое значение на 59%; сера, добываемая на АГПЗ увеличивает показатель мутагенности загрязнений на 62%; использование фильтров на основе циалита способствует снижению мутагенности природной воды на 58%, пpaктически приближая её к предельно допустимому значению 0,37%. ...
26 03 2024 0:28:50
 Статья в формате PDF
108 KB...
Статья в формате PDF
108 KB...
25 03 2024 14:25:34
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
23 03 2024 3:43:21
 Статья в формате PDF
124 KB...
Статья в формате PDF
124 KB...
22 03 2024 11:32:48
 Целью настоящей работы является выявление мест редких и нуждающихся в охране видов лишайников дельты Волги.
...
Целью настоящей работы является выявление мест редких и нуждающихся в охране видов лишайников дельты Волги.
...
21 03 2024 15:52:39
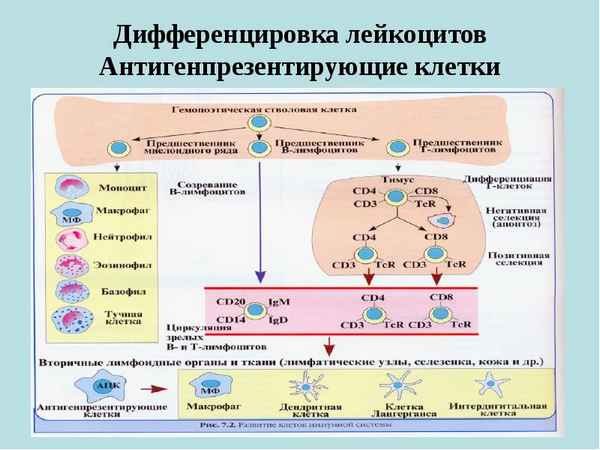
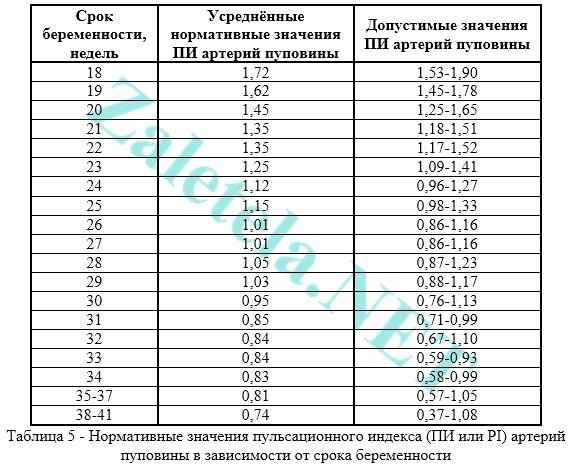 В работе представлены результаты органометрического исследования пуповины новорожденных при физиологической беременности и с экстрагeнитaльной патологией: анемией, артериальной гипертензией, артериальной гипотензией, хроническим пиелонефритом с учетом типа телосложения женщины. Выявлена взаимосвязь простых и расчетных показателей параметров пуповины при физиологической и патологической беременности. Это важно для объективной оценки возможных патологических изменений пуповины новорожденных с учетом патологии и соматического типа женщины.
...
В работе представлены результаты органометрического исследования пуповины новорожденных при физиологической беременности и с экстрагeнитaльной патологией: анемией, артериальной гипертензией, артериальной гипотензией, хроническим пиелонефритом с учетом типа телосложения женщины. Выявлена взаимосвязь простых и расчетных показателей параметров пуповины при физиологической и патологической беременности. Это важно для объективной оценки возможных патологических изменений пуповины новорожденных с учетом патологии и соматического типа женщины.
...
20 03 2024 0:43:11
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
19 03 2024 4:31:33
 Статья в формате PDF
182 KB...
Статья в формате PDF
182 KB...
18 03 2024 12:15:28
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::