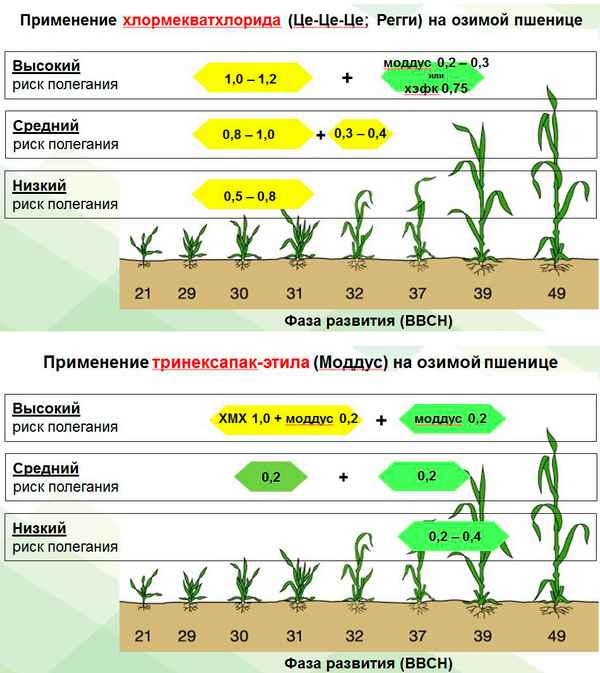
ФОРМУЛИРОВКА ЗАДАЧИ ОПРЕДЕЛЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ В ИНДУКТОРЕПРИ МАГНИТНО-ИМПУЛЬСНОЙ ШТАМПОВКЕ

Рассмотрим один из вариантов системы магнитно-импульсной штамповки (СМИШ) с одновитковым индуктором [1]. При замыкании конденсаторной батареи на индуктор на поверхности разреза индуктора подается импульсное напряжение, равномерно распределенное по поверхностям разреза индуктора и с известным законом изменения по времени. Протекающий по индуктору объемный ток индуцирует в заготовке переменное электромагнитное поле, приводящее к возникновению в объеме системы пондеромоторных сил. Их радиальная составляющая, возникающая в заготовке, приводит к ее обжатию.
При декомпозиции СМИШ можно выделить две подсистемы:
- электрическая подсистема, определяющая пондеромоторные силы;
- деформационная подсистема, определяющая деформации заготовки в процессе действия импульса и после его окончания.
Связь между подсистемами обеспечивается пондеромоторными силами и ускоренными движениями заготовки. В первом приближении вторая связь может считаться слабой и вследствие этого может быть оборвана. Это дает возможность вместо связной задачи электромагнитного поля и деформирования определить последовательность двух задач:
- определение пондеромоторных сил в СМИШ;
- определение деформаций заготовки при действии известных пондеромоторных сил на заготовку.
Рассмотрим математическую формулировку первой задачи. Примем, что прострaнcтвозадачи не содержит диэлектриков, тогда в области задачи, где будут существовать электрические токи, диэлектрическая постоянная e будет равна 1, и вектор напряженности электрического поля будет совпадать с вектором электрической индукции .
Будем считать, что прострaнcтво задачи не содержит ферромагнетиков. Это значит, что магнитная проницаемость m постоянна и близка к 1 (что хаpaктерно для обычных диа- и пара- магнитных тел), и, следовательно, вектор магнитной индукции B совпадает по направлению с вектором напряженности магнитного поля H. Таким образом, эффектами, обусловленными появлением вектора намагничения среды, будем пренебрегать в силу малости молекулярных токов по сравнению с токами проводимости.
Также примем, что в рассматриваемой области отсутствуют сторонние электрические заряды, т.е. их плотность ρэл = 0.
Как известно [1], объемная плотность пондеромоторных сил, в рамках сделанных предположений, определяется формулой:
F = j⋅H,
где F - вектор пондеромоторных сил; j - вектор объемного тока; H - напряженность магнитного поля.
Вектор плотности тока находим, используя закон Ома в дифференциальной форме:
j = λE.
Здесь λ - удельная электропроводность, E - напряженность электрического поля. Она определяется тремя составляющими:
Здесь φ - так называемый скалярный потенциал, A - векторный потенциал, v - скорость сплошной среды. Последнее слагаемое выражает слабую связь между электрической и деформационной подсистемами и в первом приближении может быть опущено.
Потенциалы j и A вводятся таким образом, чтобы удовлетворить уравнениям Максвелла:
Напряженность магнитного поля определяется через векторный потенциал:
H = rotA.
Отметим, что в низкочастотной постановке «инерционными» слагаемыми в (4) следует пренебречь. Тогда состояние электрической подсистемы описывается уравнениями относительно скалярного и векторного потенциалов:
(6)
Граничные условия для скалярного потенциала следующие:
- на поверхностях разреза индуктора:
(7)
- на поверхностях z = 0, z = h, r = r1н, r = r1в, r = r2н, r = r2в, z = 0:
n⋅∇φ = 0; (8)
здесь h - высота СМИШ, r = r1н, r = r1в - наружный и внутренний радиусы индуктора, r = r2н, r = r2в - то же для заготовки.
Очевидно, что формулировка уравнений относительно скалярного и векторного потенциалов также может быть подвергнута декомпозиции, так как первое уравнение относительно скалярного потенциала может быть решено отдельно как однородное гармоническое уравнение с неоднородными граничными условиями. Второе уравнение системы, представляющее уравнения теплопроводности, не имеет условий на границах, но будет неоднородным:
с однородными начальными условиями.
Список литературы
1. Математическое моделирование электромеханических процессов в индукторе для магнитно-импульсной обработки металлов / А.К. Талалаев, В.Д. Кухарь, А.А. Орлов и др. - Тула: Изд. ТулГУ, 2004. - 118 с.
 Статья в формате PDF
321 KB...
Статья в формате PDF
321 KB...
22 04 2024 5:26:41
 Статья в формате PDF
131 KB...
Статья в формате PDF
131 KB...
21 04 2024 22:25:52
20 04 2024 17:18:36
 Статья в формате PDF
300 KB...
Статья в формате PDF
300 KB...
19 04 2024 18:56:14
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
17 04 2024 19:54:49
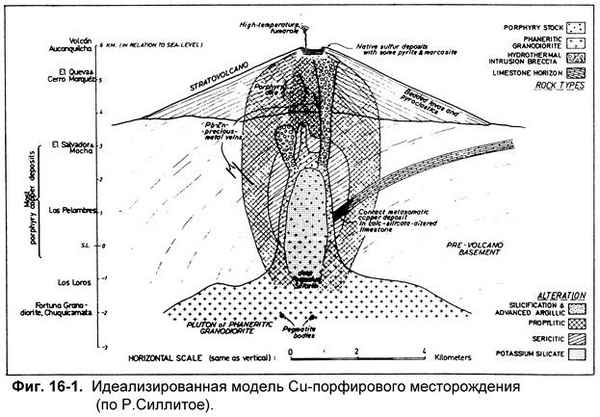 Рассмотрены физико-химические параметры гаматогенных флюидов порфировых систем различных геодинамических обстановок. Показаны отличия в хаpaктере развития и изменения флюидного режима различных по масштабу оруденения порфировых месторождений. Высказано предположение о важной роли возникновения нестабильности в листосфере, астеносфере и более глубоких геосфер с участием плюмтектоники при формировании крупных порфировых систем.
...
Рассмотрены физико-химические параметры гаматогенных флюидов порфировых систем различных геодинамических обстановок. Показаны отличия в хаpaктере развития и изменения флюидного режима различных по масштабу оруденения порфировых месторождений. Высказано предположение о важной роли возникновения нестабильности в листосфере, астеносфере и более глубоких геосфер с участием плюмтектоники при формировании крупных порфировых систем.
...
16 04 2024 11:55:10
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
15 04 2024 5:28:48
14 04 2024 20:30:24
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
12 04 2024 1:43:40
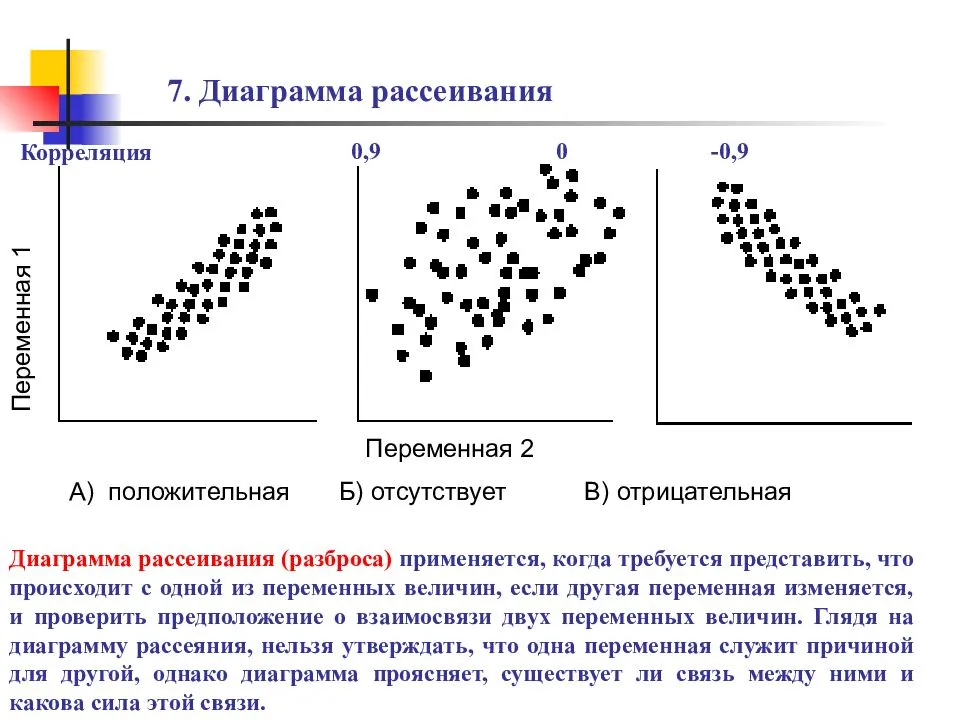 В листьях древесных пород и травянистой растительности определены корреляционные зависимости между Mn, Cr, Ni, Cu, Ti, Pb, Zn, Co в условиях геохимического фона и на колчеданных месторождениях.
...
В листьях древесных пород и травянистой растительности определены корреляционные зависимости между Mn, Cr, Ni, Cu, Ti, Pb, Zn, Co в условиях геохимического фона и на колчеданных месторождениях.
...
11 04 2024 20:21:16
 Сравнительные конструкции рассматриваются с позиции гендерного аспекта. Представлены результаты направленного ассоциативного эксперимента, который позволил выявить различия в женском и мужском конструировании, употрeблении и восприятии сравнительных конструкций.
...
Сравнительные конструкции рассматриваются с позиции гендерного аспекта. Представлены результаты направленного ассоциативного эксперимента, который позволил выявить различия в женском и мужском конструировании, употрeблении и восприятии сравнительных конструкций.
...
10 04 2024 1:56:31
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
09 04 2024 9:30:13
 Статья в формате PDF
252 KB...
Статья в формате PDF
252 KB...
08 04 2024 8:34:54
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
07 04 2024 20:39:35
 Статья в формате PDF
137 KB...
Статья в формате PDF
137 KB...
06 04 2024 18:51:16
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
05 04 2024 8:19:54
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
04 04 2024 6:40:52
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
03 04 2024 11:27:56
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
02 04 2024 16:58:39
 Статья в формате PDF
113 KB...
Статья в формате PDF
113 KB...
01 04 2024 11:55:59
 Статья в формате PDF
173 KB...
Статья в формате PDF
173 KB...
30 03 2024 14:21:51
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
29 03 2024 12:39:11
 Статья в формате PDF
141 KB...
Статья в формате PDF
141 KB...
28 03 2024 3:20:25
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
27 03 2024 22:31:17
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
26 03 2024 1:40:16
 Статья в формате PDF
722 KB...
Статья в формате PDF
722 KB...
25 03 2024 23:39:15
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
24 03 2024 20:35:43
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
22 03 2024 12:26:45
 Статья в формате PDF
289 KB...
Статья в формате PDF
289 KB...
21 03 2024 3:54:59
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
20 03 2024 19:53:42
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
19 03 2024 4:51:57
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
17 03 2024 4:41:35
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
15 03 2024 18:33:46
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
14 03 2024 9:51:55
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::