АСИМПТОТИКА СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА ДЕСЯТОГО ПОРЯДКА С СУММИРУЕМЫМ ПОТЕНЦИАЛОМ

Рассмотрим дифференциальное уравнение вида
(1)
где λ - спектральный параметр, функция q(x) называется потенциалом.
Дифференциальное уравнение (1) мы будем рассматривать вместе с граничными условиями следующего вида:
(2)
где
Мы будем предполагать, что потенциал является суммируемой функцией на отрезке
почти всюду на отрезке . (3)
Дифференциальное уравнение (1) и граничные условия (2) задают дифференциальный оператор с суммируемым потенциалом.
Для изучения асимптотики собственных значений краевых задач, связанных с дифференциальным оператором (1)-(2), необходимо знать асимптотику решений дифференциального уравнения (1).
Пусть - некоторая фиксированная ветвь корня, выбранная условием . Пусть - корни десятой степени из единицы, то есть
Числа находятся на единичной окружности и делят её на десять равных частей, причём
Справедливо следующее утверждение.
Теорема 1. Общее решение дифференциального уравнения (1) имеет следующий вид:
, (4)
где - произвольные постоянные, - линейно независимые решения дифференциального уравнения (1), причём при справедливы следующие асимптотические разложения:
(5)
При этом справедливы следующие формулы:
(6)
Идею разложения вида (5) мы изложили в главе 5 монографии [1].
Автором разработан метод нахождения асимптотики собственных значений и асимптотики собственных функций краевых задач типа (1)-(2) при условии выполнения (3). Для случая n=2, другой метод был продемонстрирован в работе [2].
Теорема 2. Решение y(x,s) дифференциального уравнения (1) является решением следующего интегрального уравнения Вольтерра:
, (7)
где yk(x,s) (k=1,2,...,10) - линейно независимые решения дифференциального уравнения (1) при условии , - определитель Вронского этих решений: , при этом несложно доказать, что не зависит от x.
Из формулы (7) методом последовательных приближений Пикара можно вывести асимптотику решений дифференциального уравнения (1). При этом получатся формулы (4)-(5)-(6) теоремы 1. Для дифференциального оператора четвёртого порядка это было проделано автором в работе [3].
Подставляя формулы (4)-(5)-(6) в граничные условия (2), приходим к выводу, что верно следующее утверждение.
Теорема 3. Уравнение на собственные значения дифференциального оператора (1)-(2)-(3) имеет следующий вид:
(8)
С помощью свойств определителей доказывается следующая теорема.
Теорема 4. Уравнение (8) имеет следующий вид:
(9)
В уравнении (9) введены следующие обозначения:
Справедливы следующие формулы:
Методами работ [1] и [3] доказывается следующая теорема.
Теорема 5. Асимптотика собственных значений краевой задачи (1)-(2)-(3) в первом секторе индикаторной диаграммы имеет следующий вид:
(10)
(11)
Формулы, аналогичные формулам (10)-(11), для краевых задач типа
(1)-(2)-(3), получены автором и для случаев дифференциальных операторов шестого и восьмого порядков.
Формул (10) и (11) достаточно для вычисления первого регуляризованного следа дифференциального оператора (1)-(2)-(3).
СПИСОК ЛИТЕРАТУРЫ
- Митрохин С. И. Спектральная теория операторов: гладкие, разрывные, суммируемые коэффициенты. М.: ИНТУИТ, 2009. - 364 с.
- Винокуров В. А., Садовничий В. А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Серия: матем. - 2000. - Т. 64, №4. - С. 47-108.
- Митрохин С. И. Асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами. - Вестник Моск. ун-та. Сер.1, математика, механика. - 2009. - №3. - С. 14-17.
 Статья в формате PDF
130 KB...
Статья в формате PDF
130 KB...
09 03 2026 12:53:14
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
07 03 2026 7:23:35
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
06 03 2026 1:13:37
 На основе введённых функций состояния для электромагнитного поля и зарядовой функции состояния для частиц выведена полная система уравнений Максвелла для электродинамики. Показано, что закон сохранения зарядов есть следствие существования этой функции. Показано также, что в вакууме электромагнитное поле отсутствует, что подтверждает справедливость теории дальнодействия.
...
На основе введённых функций состояния для электромагнитного поля и зарядовой функции состояния для частиц выведена полная система уравнений Максвелла для электродинамики. Показано, что закон сохранения зарядов есть следствие существования этой функции. Показано также, что в вакууме электромагнитное поле отсутствует, что подтверждает справедливость теории дальнодействия.
...
05 03 2026 1:55:52
 Статья в формате PDF
130 KB...
Статья в формате PDF
130 KB...
04 03 2026 21:16:59
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
03 03 2026 23:44:16
 Статья в формате PDF
278 KB...
Статья в формате PDF
278 KB...
02 03 2026 9:45:43
 Статья в формате PDF
290 KB...
Статья в формате PDF
290 KB...
01 03 2026 6:19:50
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
28 02 2026 19:12:58
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
27 02 2026 14:34:49
 Статья в формате PDF
163 KB...
Статья в формате PDF
163 KB...
26 02 2026 16:24:15
 Статья в формате PDF
125 KB...
Статья в формате PDF
125 KB...
25 02 2026 22:41:50
 Статья в формате PDF
266 KB...
Статья в формате PDF
266 KB...
24 02 2026 21:44:22
 В работе приводится краткий обзор достижений регенеративной медицины. Что представляет из себя регенеративная медицина, насколько реально применение ее разработок в нашей жизни? Как скоро мы сможем воспользоваться ими? На эти и другие вопросы сделана попытка ответить в данной работе.
...
В работе приводится краткий обзор достижений регенеративной медицины. Что представляет из себя регенеративная медицина, насколько реально применение ее разработок в нашей жизни? Как скоро мы сможем воспользоваться ими? На эти и другие вопросы сделана попытка ответить в данной работе.
...
23 02 2026 10:39:38
 Статья в формате PDF
137 KB...
Статья в формате PDF
137 KB...
22 02 2026 22:36:24
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
21 02 2026 6:36:27
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
20 02 2026 10:50:24
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
19 02 2026 0:36:14
 Статья в формате PDF
245 KB...
Статья в формате PDF
245 KB...
18 02 2026 1:24:23
 Статья в формате PDF
154 KB...
Статья в формате PDF
154 KB...
17 02 2026 15:44:29
16 02 2026 2:37:29
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
15 02 2026 16:45:35
 Статья в формате PDF
626 KB...
Статья в формате PDF
626 KB...
14 02 2026 3:58:52
 Статья в формате PDF
133 KB...
Статья в формате PDF
133 KB...
13 02 2026 17:15:47
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
12 02 2026 17:55:34
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
11 02 2026 19:49:58
 Статья в формате PDF
257 KB...
Статья в формате PDF
257 KB...
10 02 2026 19:10:25
 Статья в формате PDF
452 KB...
Статья в формате PDF
452 KB...
09 02 2026 16:26:40
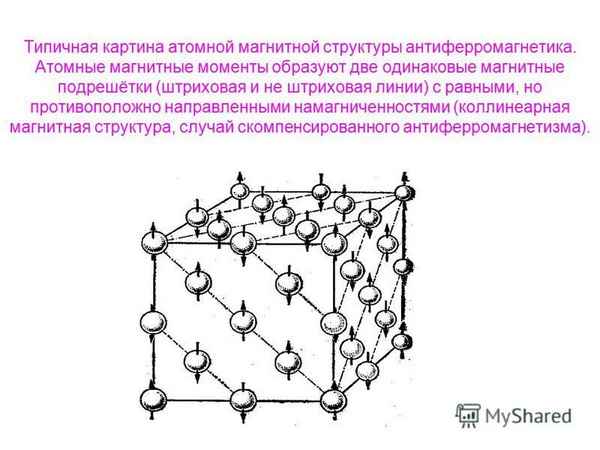 На основе анализа s-d обменного взаимодействия в структурах типа NiAs с частично вакантными катионными позициями, моделировались различного рода зависимости результирующей намагниченности от температуры нестехиометрических ферримагнетиков. На основе исследований пирротина методами ЯГР и РФА доказано, что двухподрешеточный ферримагнетик, содержащий в структуре катионные вакансии, должен рассматриваться, при определенном типе распределения вакансий, как ферримагнетик с четырьмя магнитными подрешетками. В данном случае, дополнительные магнитные подрешетки можно рассматривать как подрешетки, индуцированные хаpaктером распределения катионных вакансий в структуре. Квантово-механические расчеты в рамках модели молекулярного поля температурных изменений намагниченности отдельно для каждой из подрешеток, а также анализ результирующей термокривой намагниченности, объясняют ряд экспериментально полученных кривых зависимости намагниченности от температуры нестехиометрического пирротина с различной плотностью вакансий в структуре.
...
На основе анализа s-d обменного взаимодействия в структурах типа NiAs с частично вакантными катионными позициями, моделировались различного рода зависимости результирующей намагниченности от температуры нестехиометрических ферримагнетиков. На основе исследований пирротина методами ЯГР и РФА доказано, что двухподрешеточный ферримагнетик, содержащий в структуре катионные вакансии, должен рассматриваться, при определенном типе распределения вакансий, как ферримагнетик с четырьмя магнитными подрешетками. В данном случае, дополнительные магнитные подрешетки можно рассматривать как подрешетки, индуцированные хаpaктером распределения катионных вакансий в структуре. Квантово-механические расчеты в рамках модели молекулярного поля температурных изменений намагниченности отдельно для каждой из подрешеток, а также анализ результирующей термокривой намагниченности, объясняют ряд экспериментально полученных кривых зависимости намагниченности от температуры нестехиометрического пирротина с различной плотностью вакансий в структуре.
...
08 02 2026 12:40:22
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
07 02 2026 7:42:49
 Статья в формате PDF
116 KB...
Статья в формате PDF
116 KB...
06 02 2026 1:51:17
 Статья в формате PDF
110 KB...
Статья в формате PDF
110 KB...
05 02 2026 6:37:13
 В статье описаны эксперименты по изучению влияния основных факторов среды на жизнедеятельность жабронога стрептоцефалюса. Установлено, что наиболее оптимальная температура воды для роста и развития рачка и созревания его яиц составляет 15 - 25°С. Этот вид является исключительно пресноводным и чувствительно реагирует даже на небольшое повышение солености (в пределах 1 - 2%о). Однако жаброног способен выдерживать значительный дефицит кислорода в воде (2,5 - 2 мг/л).
...
В статье описаны эксперименты по изучению влияния основных факторов среды на жизнедеятельность жабронога стрептоцефалюса. Установлено, что наиболее оптимальная температура воды для роста и развития рачка и созревания его яиц составляет 15 - 25°С. Этот вид является исключительно пресноводным и чувствительно реагирует даже на небольшое повышение солености (в пределах 1 - 2%о). Однако жаброног способен выдерживать значительный дефицит кислорода в воде (2,5 - 2 мг/л).
...
04 02 2026 8:27:45
 Статья в формате PDF
292 KB...
Статья в формате PDF
292 KB...
02 02 2026 22:56:53
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
01 02 2026 10:19:56
 Статья в формате PDF
240 KB...
Статья в формате PDF
240 KB...
30 01 2026 6:50:13
 Статья в формате PDF
246 KB...
Статья в формате PDF
246 KB...
29 01 2026 11:52:22
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::




