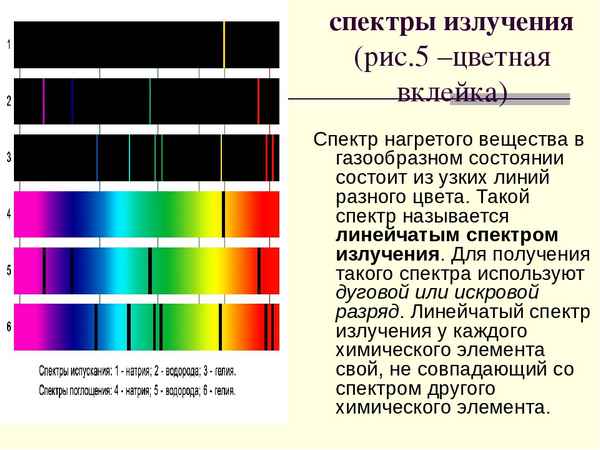
К МЕТОДИКЕ ТЕОРЕТИЧЕСКОГО ПОСТРОЕНИЯ СПЕКТРА ИЗЛУЧЕНИЯ ЛЮМИНОФОРА
Введение
Не может вызывать споров утверждение о том, что расширенный спектр излучения люминофора обусловлен влиянием внутренних напряжений, локализующихся в области энергоемких структурных дефектов - дислокаций. Возбуждение люминесценции в люминесцентных лампах осуществляется ультрафиолетовым излучением, частичная потеря их энергии происходит на структурных дефектах люминофора. Физическая причина расширения спектра заключается только в том, что поля внутренних напряжений вокруг дислокаций обуславливают изменения ширины запрещенной полосы, изменение энергетических уровней и возможных переходов оптических электронов [1]. Соответственно изменению ширины запрещенной полосы изменяются межуровневые энергетические переходы между стабильными и возмущенными уровнями активаторных центров свечения. При этом изменяются как вероятности актов возбуждения, так и величины энергий излучаемых квантов, которые поддаются расчетным оценкам. В настоящем сообщении предлагается способ расчетного построения спектра излучения люминофора (галофосфата кальция), для которого необходимо знание только положение максимумов излучения каждого из соактиваторов сурьмы и марганца и данных расчетных оценок ширины запрещенной полосы и межуровневых энергетических переходов электронов указанных центров излучения.
Теоретическая база построения расчетного спектра излучения
Ширина запрещенной полосы галофосфатного люминофора в бездефектной области Е0 составляет 8 eV [2]. Ее изменение в области локализации дислокаций δЕД расчитавается по известной формуле Ансельма, основанной на теории деформационного потенциала [2]:
δЕД = Е0 ± Е1(b/r) Cos ө; (1)
где (b/r) Cos ө - величина дилатации в области локализации дефекта, b - вектор Бюргерса дислокации, принимаемый равным параметру решетки галофосфатного люминофора 1·10-9 м, r - расстояние до места в решетке, где оценивается величина δЕД, ө - величина угла между положительным направлением экстраплоскости дислокации и направлением радиус-вектора в точку расчета δЕД. Величина Е1 по Ансельму хаpaктеризуется, как энергия взаимодействия электрона с колебаниями решетки и имеет вид:
Е1 = (h2/4π2)/(3ma2); (2)
В (2) h - постоянная Планка, m - масса электрона, a- по Ансельму уже величина параметра кристаллической решетки. В отношении последней величины мы посчитали верным уточнение следующего порядка. Поскольку Е1 определяет взаимодействие электрона с колебаниями решетки, то верным будет в (2) проставлять не параметр решетки, а величину средней амплитуды колебаний L, поскольку только амплитуда колебаний определяет энергию колебаний. По результатам сравнения зависимости от расстояния до дефекта величины δЕД и величины напряжения от дислокации σ, можно показать, что средняя амплитуда колебаний для данного люминофора может быть принята равной L = 0,001a.
Методика построения теоретического спектра излучения
Поскольку составляющие сурьмяная и марганцевая полосы уширенного экспериментально измеренного спектра симметричны относительно максимумов излучения, можно принять распределение интенсивности в них соответствующим функции Гаусса. Энергия кванта излучения cвязана с длиной волны соотношением:
hν =hс/λ; (3)
где ν - частота световых колебаний, а с - скорость света. От положения длины волны λ0 каждого из соактиваторов сурьмы и марганца влево и вправо на расстояние δλi = 10 нм последовательно находим величины новых квантов (hν)i = (hν)0 ± (δhν)i, где (hν)0 - величина кванта, соответствующая положению максимума излучения λ0. В связи с тем, что длина волны при этом изменяется, каждая следующая величина (hν)i будет все больше изменятьться на каждое новое значение (δhν)i по отношению к значению (hν)0 и будет равна каждому новому измененному значению межуровневого расстояния между энергиями стабильного и возмущенного уровней соактиваторов Sb и Mn. Эти новые межуровневые расстояния увеличиваются (уменьшаются) пропорционально изменению ширины запрещенной полосы по выражению (1), поэтому легко поддаются количественной оценке. Но с изменением межуровневого расстояния и все большим изменением расстояния между возмущенным и стабильным уровнями при постоянной величине кванта возбуждающего ультрафиолетового излучения резко снижается вероятность осуществления актов возбуждения центров свечения pi, поскольку кванту ультрафиолета все труднее «доставать» удаляющийся верхний уровень энергии, или все легче «перебрасыватся» в зону проводимости. По аналогии с другими энергоактивируемыми процессами [4] (диффузией, испарением и пр.) для величины вероятности свершения актов возбуждения и излучения pi можно записать:
pi =exp(-(hν)i2/(hν)02); (4)
Величину относительной интенсивности излучения определим через произведение числа переходов на вероятность излучательной рекомбинации:
Jотн = С·(hν)0·exp(-(hν)i2/(hν)02)); (5)
где С - концентрация каждого из соактиваторов в процентах.
Обсуждение результатов расчетных оценок
Сопоставление экспериментально полученной с помощью спектроскопических измерений [2] и расчетным путем построенной с ипользованием уточненной формулы Ансельма спектральных полос излучения галофосфатного люминофора с активаторными центрами свечения Sb и Mn позволяет высказать следующие замечания.
Предлагаемая методика позволяет получать принципиальную возможность расчетного построения спектра излучения при условии надежных данных относительно концентрации активаторов и аналитической формы распределения интенсивности линий спектра. На начальном этапе этих исследований не следует ожидать точного совпадения экспериментальной и расчетной полос излучения люминесценции. Расчетный спектр может оказаться существенно более измененным по отношению к экспериментальному и это возможно по нескольким причинам. Пока невозможно учесть все факторы, которые влияют на параметры спектров и, прежде всего, на соотношение максимумов излучения соактиваторов сурьмы и марганца. По данным работы Гугеля [2] на спектр излучения оказывает существенное влияние не только соотношение концентраций соактиваторов Sb и Mn, но и соотношение входящих в химическую формулу люминофора ионов галогенов фтора и хлора и даже примесных фаз. Кроме того, на форму расширенного спектра существенное влияние оказывает плотность дислокаций и хаpaктер их распределения в решетке люминофора. Возможны и другие причины.
СПИСОК ЛИТЕРАТУРЫ
- Никитенко В.И., Осипьян Ю.А. Влияние дислокаций на оптические, электрические и магнитные свойства кристаллов. Проблемы современной кристаллографии. «Наука». 1975.- С. 239-261.
- Гугель Б.М. Люминофоры для электровакуумной промышленности. М.: «Энергия»,1967.- 344 с.
- Ансельм А.П. Введение в теорию полупроводников. М.:Мир.1972. -386с.
- Герцрикен С.Д., Дехтяр И.Я. Диффузия в металлах и сплавах в твердой фазе. М.: «Физматгиз».- 1960.- 564 с.
 Рассмотрены перспективные площади поисков залежей колчеданов в Орской и Бакайской синклиналях и в Западном Примугоджарье по гидрогеологическим показателям. Купоросные воды - реликтовые спутники сульфидных залежей, видимо широко развиты среди вулканитов девонского рифта Урала.
...
Рассмотрены перспективные площади поисков залежей колчеданов в Орской и Бакайской синклиналях и в Западном Примугоджарье по гидрогеологическим показателям. Купоросные воды - реликтовые спутники сульфидных залежей, видимо широко развиты среди вулканитов девонского рифта Урала.
...
25 04 2024 19:13:34
 Статья в формате PDF
112 KB...
Статья в формате PDF
112 KB...
24 04 2024 3:14:41
 Статья в формате PDF
244 KB...
Статья в формате PDF
244 KB...
23 04 2024 4:36:33
 Статья в формате PDF
253 KB...
Статья в формате PDF
253 KB...
22 04 2024 20:39:20
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
21 04 2024 15:57:51
 Статья в формате PDF
114 KB...
Статья в формате PDF
114 KB...
20 04 2024 7:49:33
 Статья в формате PDF
122 KB...
Статья в формате PDF
122 KB...
19 04 2024 4:39:29
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
18 04 2024 22:52:39
 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
17 04 2024 22:16:44
 Статья в формате PDF
270 KB...
Статья в формате PDF
270 KB...
16 04 2024 22:43:43
 Статья в формате PDF
365 KB...
Статья в формате PDF
365 KB...
15 04 2024 13:13:11
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
14 04 2024 13:49:32
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
13 04 2024 11:56:33
 Статья в формате PDF
126 KB...
Статья в формате PDF
126 KB...
12 04 2024 9:11:36
 Изучено влияние солей кадмия, свинца и марганца на содержание белков в сыворотке крови сеголеток карпа. Показаны разнонаправленные изменения белкового состава сыворотки крови рыб при воздействии солей тяжелых металлов, о чем можно судить на основании изменения А/G индекса. При хроническом действии ионов кадмия отмечено значительное преобладание суммарного содержания альбуминов над глобулинами на протяжении всего эксперимента, пребывание рыб в среде с ионами свинца сопровождалось более значительным ростом содержания глобулинов, тогда как при действии ионов марганца не выявлен однонаправленный хаpaктер изменения соотношения альбуминов и глобулинов.
...
Изучено влияние солей кадмия, свинца и марганца на содержание белков в сыворотке крови сеголеток карпа. Показаны разнонаправленные изменения белкового состава сыворотки крови рыб при воздействии солей тяжелых металлов, о чем можно судить на основании изменения А/G индекса. При хроническом действии ионов кадмия отмечено значительное преобладание суммарного содержания альбуминов над глобулинами на протяжении всего эксперимента, пребывание рыб в среде с ионами свинца сопровождалось более значительным ростом содержания глобулинов, тогда как при действии ионов марганца не выявлен однонаправленный хаpaктер изменения соотношения альбуминов и глобулинов.
...
11 04 2024 19:53:59
 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
10 04 2024 9:28:26
 Статья в формате PDF
184 KB...
Статья в формате PDF
184 KB...
09 04 2024 13:41:36
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
08 04 2024 2:20:21
 Статья в формате PDF
383 KB...
Статья в формате PDF
383 KB...
07 04 2024 3:12:26
 8 февраля 2004 года исполняется 75 лет со дня рождения и 60 лет педагогической, производственной деятельности академика Российской Академии естествознания, Академии эмалирования России, Заслуженного деятеля науки и техники РФ, почетного работника высшего образования России, доктора технических наук, профессора кафедры технологии керамики, стекла и вяжущих веществ ЮРГТУ (НПИ).
...
8 февраля 2004 года исполняется 75 лет со дня рождения и 60 лет педагогической, производственной деятельности академика Российской Академии естествознания, Академии эмалирования России, Заслуженного деятеля науки и техники РФ, почетного работника высшего образования России, доктора технических наук, профессора кафедры технологии керамики, стекла и вяжущих веществ ЮРГТУ (НПИ).
...
06 04 2024 6:55:45
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
05 04 2024 12:47:36
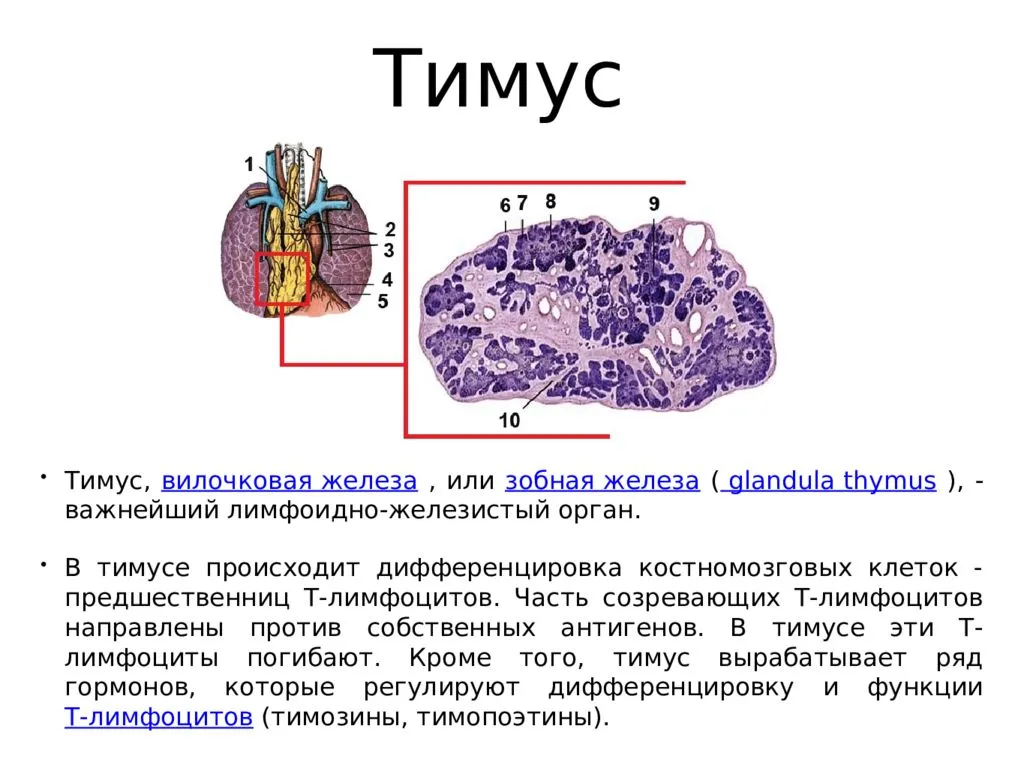 Разделение тимуса на истинные доли происходит у плодов белой крысы в процессе его неравномерного роста в плотном окружении, под давлением ветвей внутренней грудной артерии и сопровождающих вен.
...
Разделение тимуса на истинные доли происходит у плодов белой крысы в процессе его неравномерного роста в плотном окружении, под давлением ветвей внутренней грудной артерии и сопровождающих вен.
...
04 04 2024 12:36:13
В работе на созданных молекулярно-генетических моделях выявлена ассоциация генотипа А2/А2 локуса TAG 1A гена рецептора дофамина второго типа крыс с повышенной аудиогенной чувствительностью и увеличением удельной площади базолатеральной группировки миндалевидного комплекса по сравнению с крысами А1/А1. ...
03 04 2024 10:22:56
 Статья в формате PDF
120 KB...
Статья в формате PDF
120 KB...
02 04 2024 23:46:22
31 03 2024 13:46:30
 Статья в формате PDF
285 KB...
Статья в формате PDF
285 KB...
30 03 2024 15:27:31
 Статья в формате PDF
118 KB...
Статья в формате PDF
118 KB...
29 03 2024 5:23:53
 Статья в формате PDF
134 KB...
Статья в формате PDF
134 KB...
28 03 2024 3:12:49
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
27 03 2024 4:26:12
 Статья в формате PDF
199 KB...
Статья в формате PDF
199 KB...
26 03 2024 10:27:55
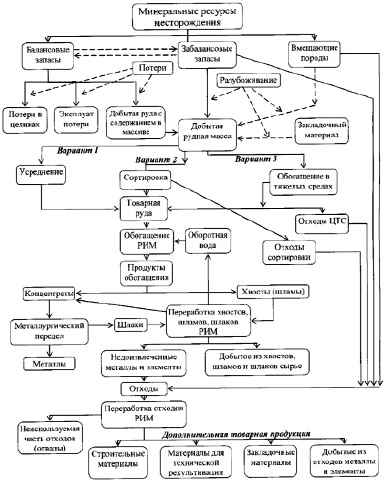 На основе анализа литературных источников показана необходимость создания эффективных методов переработки руд цветных металлов. Описано отрицательное воздействие горнообогатительного производства на окружающую среду. Рассмотрены проблемы освоения месторождений сырья и предложены пути их решения. Приведена схема рационального освоения минеральных ресурсов рудного месторождения с применением разрядноимпульсных методов. Обоснована возможность использования разрядноимпульсных воздействий в обогатительных процессах, что позволит повысить полноту извлечения полезных компонентов при переработке минерального сырья. Выделены ограничения применения импульсных методов. Установлено, что разрядноимпульсные методы интенсифицируют избирательное раскрытие минеральных ассоциаций во всем диапазоне исходных классов крупности. Эти методы эффективны в комбинированных схемах переработки труднообогатимых руд сложного состава. Применение комбинированных схем позволит сократить на 10–15 % время измельчения до выхода контрольного класса.
...
На основе анализа литературных источников показана необходимость создания эффективных методов переработки руд цветных металлов. Описано отрицательное воздействие горнообогатительного производства на окружающую среду. Рассмотрены проблемы освоения месторождений сырья и предложены пути их решения. Приведена схема рационального освоения минеральных ресурсов рудного месторождения с применением разрядноимпульсных методов. Обоснована возможность использования разрядноимпульсных воздействий в обогатительных процессах, что позволит повысить полноту извлечения полезных компонентов при переработке минерального сырья. Выделены ограничения применения импульсных методов. Установлено, что разрядноимпульсные методы интенсифицируют избирательное раскрытие минеральных ассоциаций во всем диапазоне исходных классов крупности. Эти методы эффективны в комбинированных схемах переработки труднообогатимых руд сложного состава. Применение комбинированных схем позволит сократить на 10–15 % время измельчения до выхода контрольного класса.
...
25 03 2024 12:39:55
 Статья в формате PDF
141 KB...
Статья в формате PDF
141 KB...
24 03 2024 6:35:20
 Статья в формате PDF
194 KB...
Статья в формате PDF
194 KB...
23 03 2024 9:56:32
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
22 03 2024 6:15:27
 Статья в формате PDF
135 KB...
Статья в формате PDF
135 KB...
21 03 2024 13:45:25
 Статья в формате PDF
104 KB...
Статья в формате PDF
104 KB...
20 03 2024 4:55:52
 Статья в формате PDF
269 KB...
Статья в формате PDF
269 KB...
19 03 2024 14:36:36
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
18 03 2024 14:36:30
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::