СИНЕРГЕТИЧЕСКИЙ ПОДХОД К ВОПРОСАМ ОБРАЗОВАНИЯ И НАУКИ

Образование непосредственно связано с наукой, а через неё с материальным производством, с задачами преобразования природы и социальных отношений [1]. В настоящее время коренным образом меняется система научного познания. Четкие границы между пpaктической и познавательной деятельностью размываются, развиваются комплексные и междисциплинарные исследования, выделяются более новые, более сложные типы объектов познания, хаpaктеризующиеся универсальностью и сложностью организации, которые поддаются теоретическому (математическому) моделированию. Реальные системы: биологические, социальные - являются открытыми, следовательно, они обмениваются с окружающей средой веществом, энергией и информацией [2]. Для описания таких сложных, открытых, диссипативных нелинейных систем разработан математический аппарат синергетики [2].
Благодаря синергетике возможно достаточно точное количественное исследование принципов построения системы, её возникновения, развития и самоусложнения. Методами синергетики возможно моделирование сложных самоорганизующихся систем: от морфогенеза в биологии и некоторых аспектов функционирования мозга, до автоколебательных процессов в различных средах; от молекулы ДНК до эволюции объектов космических масштабов.
Синергетика позволяет понять, что существуют общие закономерности, управляющие возникновением самоорганизующихся систем, их структур и функций. Сложные диссипативные системы хаpaктеризуются большим числом степеней свободы и далеко не все одинаково важны для её функционирования. Ведущие, определяющие степени свободы, к которым и «подстраиваются» остальные, являются параметрами порядка, которые отражают содержание основания неравновесной системы. Правильно найденные соотношения между параметрами порядка позволяют значительно упростить математические модели самоорганизующихся систем. Одной из известных синергетических моделей, в частности, обучения, является следующая [3]:
(1)
где x - количественная хаpaктеристика усвоенной в процессе обучения информации;
b(t) - количественная хаpaктеристика входной информации; k - индивидуальный коэффициент восприятия информации; T3 - индивидуальное время запаздывания в восприятии информации.
Принцип построения фундаментального вуза, в отличие от прикладного, базируется на применении систем с памятью типа (1). Параметром порядка является «начальная функция» φ(t). На рис. 1 показана зависимость от времени усвоения фиксированной порции входной информации b(t) для разных значений коэффициента восприятия k и времени запаздывания T3 [3]. Анализ данной математической модели позволяет сделать вывод о том, что резерв повышения качества обучения следует искать в максимальном учете индивидуальных психологических особенностей обучаемых.
Рис. 1. Зависимости времени усвоения учебной информации
от индивидуальных показателей обучаемых
Если учесть нелинейный хаpaктер изменения коэффициента восприятия k от объема накапливаемых в процессе обучения знаний, например, в уравнении:
(2)
данном в работе [3], то можно получить решение в виде динамического хаоса (рис. 2). Возникновение динамического хаоса можно тpaктовать как необходимое условие генерации новой информации. Этот процесс позволяет использовать в фундаментальном обучении творческий хаpaктер самореализации личности студента.
Рис. 2. Динамический хаос в системе обучения
В ряде моделей учитываются материальные ресурсы, например:
(3)
где R - объем материальных ресурсов; b - параметр усвоения инноваций; Ac - критический уровень развития интеллектуальной сферы; h - возобновляемые ресурсы; tR - время «включения в работу» специалиста.
Модель показывает, что существует пороговый уровень финансирования интеллектуальной сферы, и если объем финансирования окажется ниже этого уровня, то интеллектуальная сфера быстро теряет способность играть роль ресурса развития общества [5].
В качестве моделей обучения и модели развития науки широко применяются логистические уравнения, например, нелинейное дифференциальное уравнение Риккати [4]:
(4)
На рис. 3 изображена логистическая кривая, как одно из решений системы:
(5)
В качестве x может быть величина, хаpaктеризующая отношение численности студентов, приходящихся на одного преподавателя в группе, к конкурсу в данном вузе, выраженному в величине человек/место [3]. Модель позволяет определить при каком значении численности учебной группы обучение станет качественным.
Мы рассмотрели небольшой срез синергетических моделей, анализ которых позволит дать конкретные рекомендации. Они могут быть использованы как в сфере управления и политики высшего образования, так и для педагогов пpaктиков. Кроме того, мы рекомендуем в отдельные дисциплины, читаемые студентам разных факультетов, ввести разделы, описывающие единые принципы и единую математическую модель синергетики, или ввести её как самостоятельную дисциплину.
Рис. 3. Логистическая кривая при g = 2
Список литературы
- Кутимская М.А., Бузунова М.Ю. Роль синергетики в системе образования в аграрном вузе / Система образования в аграрном вузе: проблемы и тенденции: материалы МНПК. - Иркутск: ИрГСХА, 2008. - С. 246-251.
- Кутимская М.А., Волянюк Е.Н. Бионоосфера: учеб. пособие. - Иркутск: Иркут. ун-т., 2005. - 212 с.
- Солодова Е.А. Концепция модернизации высшего образования России на основе синергетического моделирования / Синергетическая парадигма. Синергетика образования. - М.: Прогресс-Традиция, 2007. - С. 418-432.
- Расина И.В. Обыкновенные дифференциальные уравнения: Учеб.-метод. пособие. - Иркутск: СИПЭУ, 2006. - 160 с.
- Пугачёва Е.Г., Соловьяненко К.Н. Самоорганизация социально-экономических систем: учеб. пособие. - Иркутск: БГУПЭ, 2003. - 172 с.
 Статья в формате PDF
331 KB...
Статья в формате PDF
331 KB...
23 04 2024 16:42:10
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
22 04 2024 17:12:47
21 04 2024 23:10:33
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
20 04 2024 22:24:22
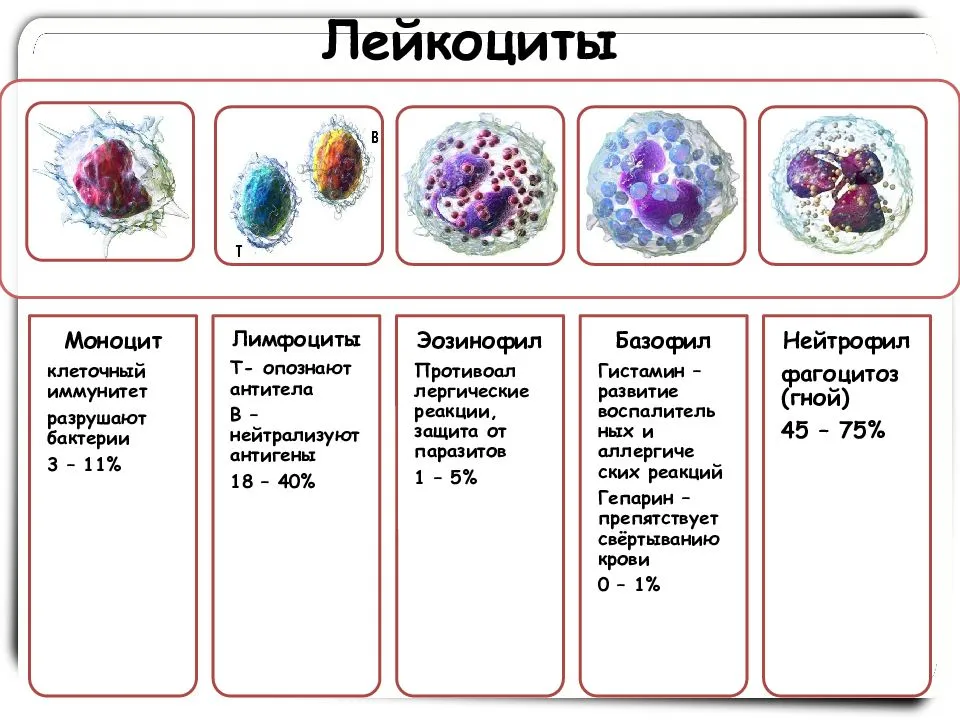 Статья в формате PDF
105 KB...
Статья в формате PDF
105 KB...
19 04 2024 18:27:19
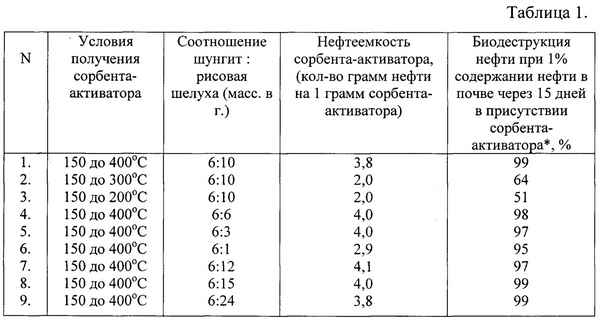 Приведен способ очистки водной поверхности от нефтяных загрязнений, который может быть использован для очистки водных объектов от пленки аварийно-разлитой и другой плавающей нефти. Разработаны математические модели процесса сорбции древесных отходов в программной среде Curve Expert 1.3.
...
Приведен способ очистки водной поверхности от нефтяных загрязнений, который может быть использован для очистки водных объектов от пленки аварийно-разлитой и другой плавающей нефти. Разработаны математические модели процесса сорбции древесных отходов в программной среде Curve Expert 1.3.
...
17 04 2024 16:26:27
 Статья в формате PDF
146 KB...
Статья в формате PDF
146 KB...
16 04 2024 11:11:45
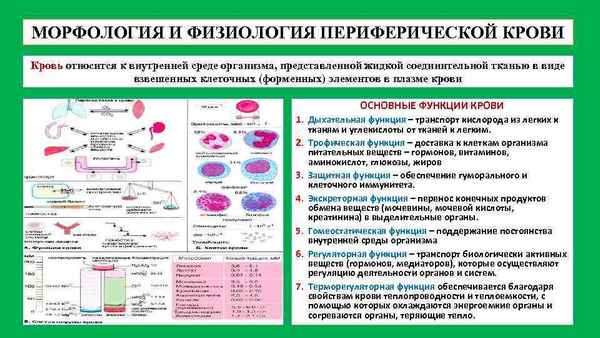 Статья в формате PDF
107 KB...
Статья в формате PDF
107 KB...
15 04 2024 5:58:38
12 04 2024 14:51:18
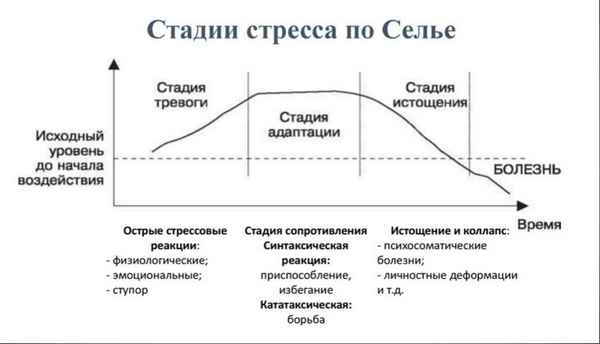 В работе исследовалось изменение метаболизма коллагена при остром стрессе у крыс с различным эмоциональным статусом. Острый стресс индуцировали, помещая животных в пластиковые камеры с отверстием для доступа воздуха на 1 час, 2,5 часа и 6 часов. Наблюдалось различие в реакции гипоталамо-гипофизарно-надпочечниковой системы и динамике показателей метаболизма коллагена у крыс с разным эмоциональным статусом.
...
В работе исследовалось изменение метаболизма коллагена при остром стрессе у крыс с различным эмоциональным статусом. Острый стресс индуцировали, помещая животных в пластиковые камеры с отверстием для доступа воздуха на 1 час, 2,5 часа и 6 часов. Наблюдалось различие в реакции гипоталамо-гипофизарно-надпочечниковой системы и динамике показателей метаболизма коллагена у крыс с разным эмоциональным статусом.
...
11 04 2024 8:34:34
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
10 04 2024 11:28:10
 Статья в формате PDF
121 KB...
Статья в формате PDF
121 KB...
09 04 2024 0:51:49
 Статья в формате PDF
117 KB...
Статья в формате PDF
117 KB...
08 04 2024 8:31:39
 Статья в формате PDF
359 KB...
Статья в формате PDF
359 KB...
07 04 2024 0:44:58
 Статья в формате PDF
359 KB...
Статья в формате PDF
359 KB...
06 04 2024 10:18:24
 Статья в формате PDF
317 KB...
Статья в формате PDF
317 KB...
03 04 2024 4:45:43
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
02 04 2024 4:36:28
 Статья в формате PDF
115 KB...
Статья в формате PDF
115 KB...
01 04 2024 8:35:53
 Статья в формате PDF
101 KB...
Статья в формате PDF
101 KB...
31 03 2024 3:16:54
 Статья в формате PDF
103 KB...
Статья в формате PDF
103 KB...
30 03 2024 11:33:33
 Статья в формате PDF
106 KB...
Статья в формате PDF
106 KB...
29 03 2024 0:58:51
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
28 03 2024 8:44:34
 Статья в формате PDF
109 KB...
Статья в формате PDF
109 KB...
26 03 2024 23:53:45
Статья в формате PDF 130 KB...
25 03 2024 10:45:20
 Статья в формате PDF
138 KB...
Статья в формате PDF
138 KB...
24 03 2024 16:15:39
 Статья в формате PDF
111 KB...
Статья в формате PDF
111 KB...
23 03 2024 5:31:58
 Статья в формате PDF
127 KB...
Статья в формате PDF
127 KB...
22 03 2024 2:41:21
 Статья в формате PDF
100 KB...
Статья в формате PDF
100 KB...
20 03 2024 9:59:32
 Статья в формате PDF
163 KB...
Статья в формате PDF
163 KB...
19 03 2024 18:19:41
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
18 03 2024 18:51:26
 Статья в формате PDF
119 KB...
Статья в формате PDF
119 KB...
17 03 2024 5:17:28
 Статья в формате PDF
129 KB...
Статья в формате PDF
129 KB...
16 03 2024 17:26:12
 Предложены офтальмологические лекарственные формы с ортофеном - глазные лекарственные пленки и пролонгированные глазные капли. Разработан их состав, технология длч производства в аптечных условиях, стандартизация. Проведены подробные биофармацевтические исследования in vitro по выбору оптимальных вспомогательных компонентов. Выбран способ количественного анализа ортофена в разработанных лекарственных форм - с помощью спектрофотометрии.
...
Предложены офтальмологические лекарственные формы с ортофеном - глазные лекарственные пленки и пролонгированные глазные капли. Разработан их состав, технология длч производства в аптечных условиях, стандартизация. Проведены подробные биофармацевтические исследования in vitro по выбору оптимальных вспомогательных компонентов. Выбран способ количественного анализа ортофена в разработанных лекарственных форм - с помощью спектрофотометрии.
...
15 03 2024 7:35:36
Еще:
Поддержать себя -1 :: Поддержать себя -2 :: Поддержать себя -3 :: Поддержать себя -4 :: Поддержать себя -5 :: Поддержать себя -6 :: Поддержать себя -7 :: Поддержать себя -8 :: Поддержать себя -9 :: Поддержать себя -10 :: Поддержать себя -11 :: Поддержать себя -12 :: Поддержать себя -13 :: Поддержать себя -14 :: Поддержать себя -15 :: Поддержать себя -16 :: Поддержать себя -17 :: Поддержать себя -18 :: Поддержать себя -19 :: Поддержать себя -20 :: Поддержать себя -21 :: Поддержать себя -22 :: Поддержать себя -23 :: Поддержать себя -24 :: Поддержать себя -25 :: Поддержать себя -26 :: Поддержать себя -27 :: Поддержать себя -28 :: Поддержать себя -29 :: Поддержать себя -30 :: Поддержать себя -31 :: Поддержать себя -32 :: Поддержать себя -33 :: Поддержать себя -34 :: Поддержать себя -35 :: Поддержать себя -36 :: Поддержать себя -37 :: Поддержать себя -38 ::